
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Chương 4: Bộ lọc số
Trong cá c phầ n trư ớ c chú ng ta đ ã tì m hiể u mộ t số cá ch biể u diễ n tí n hiệ u và hệ thố ng rờ i rạ c, đ ó là nhữ ng cô ng cụ khô ng thể thiế u trong việ c mô tả hệ thố ng xử lí tí n hiệ u. Bộ lọ c số là mộ t hệ thố ng tuyế n tí nh bấ t biế n, vì vậ y trong phầ n nà y chú ng ta sẽ sử dụ ng cá c tí nh chấ t đ ã nghiê n cứ u ở cá c phầ n trư ớ c đ ể tì m hiể u về bộ lọ c số mộ t trong nhữ ng hệ thố ng đ ư ợ c ứ ng dụ ng rấ t nhiề u trong xử lí số tí n hiệ u. Cá c bộ lọ c số dầ n đ ã thay thế cá c bộ lọ c tư ơ ng tự.
§1. Cá c bộ lọ c số lí tư ở ng
1. Khá i niê m chung
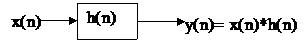 Bộ lọ c số là mộ t HT-TT-BB trong miề n thờ i gian rờ i rạ c sơ đ ồ khố i có dạ ng:
Bộ lọ c số là mộ t HT-TT-BB trong miề n thờ i gian rờ i rạ c sơ đ ồ khố i có dạ ng:
Trong miề n tầ n số đ ư ợ c đ ặ c trư ng bở i đ á p ứ ng tầ n số: H(ejw)
H(ejw) =DTFT [h(n)] = Y(ejw)/ X(ejw) = 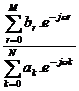
Việ c thiế t kế cá c bộ lọ c số thự c tế đ ề u đ i từ lí thuyế t cá c bọ lọ c số lí tư ở ng. Chú ng ta sẽ tì m hiể u 4 loạ i bộ lọ c số tiê u biể u là:
- Bộ lọ c số thô ng thấ p.
- Bộ lọ c số thô ng cao
- Bộ lọ c số thô ng dả i.
- Bộ lọ c số chắ n dả i.
Lọ c ở đ â y chú ng ta hiể u là lọ c tầ n số vì vậ y tấ t cả cá c đ ặ c trư ng củ a bộ lọ c số đ ề u đ ư ợ c cho theo đ á p ứ ng biê n đ ộ
2. Cá c đ ặ c trư ng củ a bộ lọ c số lí tư ở ng.
a. Bộ lọ c thô ng thấ p lí tư ở ng
Đ á p ứ ng biê n đ ộ củ a bộ lọ c thô ng thấ p lí tư ở ng đ ư ợ c đ ị nh nghĩ a như sau:
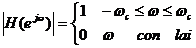
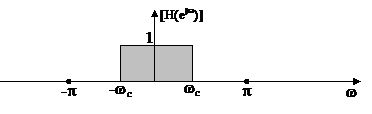 |
wc tầ n số cắ t.
[ -wc, wc ] dả i thô ng.
Nhậ n xé t: Do 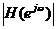 là đ ố i xứ ng do đ ó ta chỉ cầ n xé t trong mộ t nử a chu kì (p³ w³ 0) là đ ủ và coi h(n) là thự c.
là đ ố i xứ ng do đ ó ta chỉ cầ n xé t trong mộ t nử a chu kì (p³ w³ 0) là đ ủ và coi h(n) là thự c.
h(n) là biế n đ ổ i Fourier ngư ợ c củ a H(ejw)
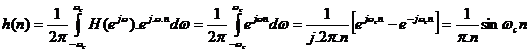
hay: 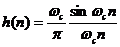 (4. 1)
(4. 1)
b. Bộ lọ c thô ng cao lí tư ỏ ng
Bộ lọ c thô ng cao lí tư ở ng là bộ lọ c mà đ á p ứ ng biê n đ ộ củ a nó đ ư ợ c đ ị nh nghĩ a như sau:
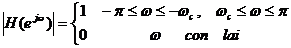
 |
wc tầ n số cắ t.
[-p, -wc]; [wc, p] dả i thô ng
Nhậ n xé t: Do 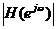 là đ ố i xứ ng do đ ó ta chỉ cầ n xé t trong mộ t nử a chu kì (p³ w³ 0) là đ ủ và coi h(n) là thự c.
là đ ố i xứ ng do đ ó ta chỉ cầ n xé t trong mộ t nử a chu kì (p³ w³ 0) là đ ủ và coi h(n) là thự c.
h(n) là biế n đ ổ i Fourier ngư ợ c củ a H(ejw)
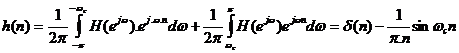
hay: 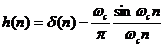 (4. 2)
(4. 2)
d(n) đ ư ợ c gọ i là đ á p ứ ng xung củ a bộ lọ c thô ng tấ t. ( All Pass Fillter ).
c. Bộ lọ c thô ng dả i lí tư ở ng.
Đ á p ứ ng biê n đ ộ củ a bộ lọ c thô ng dả i lí tư ở ng đ ư ợ c đ ị nh nghĩ a như sau:
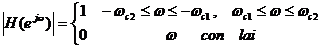
 |
wc1 tầ n số cắ t dư ớ i.
wc2 tầ n số cắ t trê n.
[-wc2, -wc1 ]; [wc1, wc2 ] dả i thô ng
Nhậ n xé t: Do 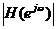 là đ ố i xứ ng do đ ó ta chỉ cầ n xé t trong mộ t nử a chu kì (p³ w³ 0) là đ ủ và coi h(n) là thự c.
là đ ố i xứ ng do đ ó ta chỉ cầ n xé t trong mộ t nử a chu kì (p³ w³ 0) là đ ủ và coi h(n) là thự c.
Nế u có 2 bộ lọ c thô ng thấ p vớ i tầ n số cắ t là wc1, và wc2 thì:
H(ejw) = H2(ejw)- H1(ejw) suy ra h(n) = h2(n) – h1(n)
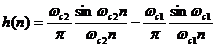 (4. 3)
(4. 3)
d. Bộ lọ c chắ n dả i lí tư ở ng.
Đ á p ứ ng biê n đ ộ củ a bộ lọ c thô ng thấ p lí tư ở ng đ ư ợ c đ ị nh nghĩ a như sau:
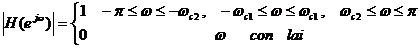
 |
wc1 tầ n số cắ t dư ớ i.
wc2 tầ n số cắ t trê n.
[-p, -wc2 ]; [-wc1, wc1 ]; [wc2, p ] dả i thô ng
Nhậ n xé t: Nế u cá c bộ lọ c thô ng tấ t và bộ lọ c thô ng dả i và bộ lọ c chắ n dả i lí tư ở ng có cù ng đ á p ứ ng pha thì ta có cá c quan hệ sau:
H(ejw) = HA(ejw)- HT(ejw) suy ra h(n) = hA(n) – hT(n)
Trong đ ó: HA(ejw) là đ á p ứ ng tầ n số củ a bộ lọ c thô ng tấ t
HT(ejw) là đ á p ứ ng tầ n số củ a bộ lọ c thô ng dả i
H(ejw) là đ á p ứ ng tầ n số củ a bộ lọ c chắ n dả i
và
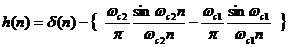 (4. 4)
(4. 4)
§2. Bộ lọ c số FIR
Trong thự c tế cá c bộ lọ c số có đ á p ứ ng tầ n số ở dạ ng:
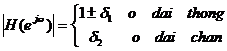
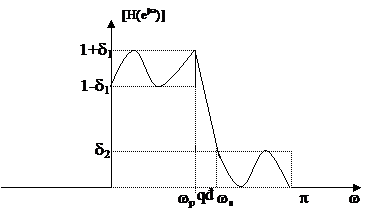 |
+ d1 đ ộ gợ n ở dả i thô ng
+ d2 đ ộ gợ n ở dả i chắ n
+ wp tầ n số giớ i hạ n dả i thô ng
+ ws tầ n số giớ i hạ n dả i chắ n
Dw = ws - wp: dả i quá đ ộ.
1. Bộ lọ c FIR thự c tế
-Trong thự c tế ta chỉ xá c đ ị nh đ ư ợ c N hệ số củ a đ á p ứ ng xung h(n). Vì vậ y khi cá c bộ lọ c FIR đ ư ợ c xâ y dụ ng dự a trê n cá c bộ lọ c số lí tư ở ng thì chú ng ta phả i:
+ Hạ n chế chiề u dà i củ a đ á p ứ ng xung bằ ng cá ch dù ng cá c hà m cử a sổ có chiề u dà i N ( rectN(n) ).
+ Chuyể n h(n) từ dạ ng khô ng nhâ n quả sang dạ ng nhâ n quả bằ ng cá ch tị nh tiế n đ i mộ t số mẫ u.
2. Cá c đ ặ c trư ng củ a bộ lọ c FIR pha tuyế n tí nh.
Coi bộ lọ c FIR có đ á p ứ ng tầ n số là H(ejw) có pha tuyế n tí nh, do đ ó nế u biế t đ á p ứ ng pha củ a nó ta sẽ biế t tí n hiệ u qua bộ lọ c vớ i đ ộ trễ nhấ t đ ị nh đ ã biế t.
Hệ thố ng FIR là hệ thố ng luô n luô n ổ n đ ị nh:
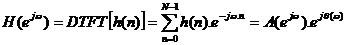
Bộ lọ c FIR có pha tuyế n tí nh nế u: 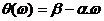 (4. 5)
(4. 5)
a. Trư ờ ng hợ p b =0
Từ (4. 5) ta có: 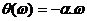
Suy ra:
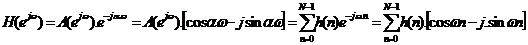
Suy ra: 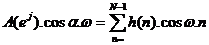 (*)
(*)
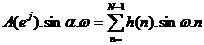 (**)
(**)
Từ (*) và (**) ta có:
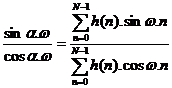
+ Nế u a = 0 thì: 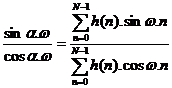 =
= 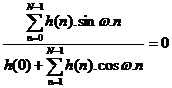
suy ra h(n) = 0 vớ i mọ i n ¹ 0 và giá trị h(0) tuỳ ý vớ i n=0. Đ â y là trư ờ ng hợ p h(n) tầ m thư ờ ng, khô ng cho chú ng ta kế t quả gì.
+ Nế u a ¹ 0 thì 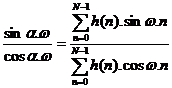 ta viế t lạ i như sau:
ta viế t lạ i như sau:
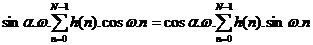 Đ ư a sina. w, cosa. w và o trong tổ ng ta có:
Đ ư a sina. w, cosa. w và o trong tổ ng ta có:
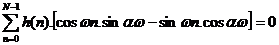 Vậ y ta có:
Vậ y ta có:
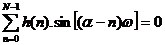
Phư ơ ng trì nh nà y có dạ ng củ a mộ t chuỗ i Fourier. Nghiệ m củ a nó có dạ ng như sau: 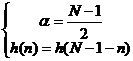
Nhậ n xé t:
- Vớ i mộ t giá trị củ a N, chỉ có duy nhấ t mộ t giá trị a đ ể đ ả m bả o q(w)=-aw là tuyế n tí nh.
- Vớ i giá trị a nà y đ á p ứ ng xung h(n) = h(N-1-n) là đ ố i xứ ng.
- Nế u N lẻ thì a là mộ t số nguyê n và tâ m đ ố i xứ ng củ a h(n) là mẫ u thứ (N-1)/2. Ta có bộ lọ c FIR loạ i 1.
- Nế u N chẵ n thì a là mộ t số khô ng nguyê n và tâ m đ ố i xứ ng củ a h(n) nằ m giữ a mẫ u thứ (N-1)/2 và N/2. Ta có bộ lọ c FIR loạ i 2.
Đ ặ c đ iể m quan trọ ng củ a bộ lọ c số FIR loạ i 1 và 2 là tí nh đ ố i xứ ng củ a đ á p ứ ng xung h(n) có rấ t nhiề u ứ ng dụ ng quan trọ ng ta sẽ xé t sau.
Ví dụ: N=6, 7
b. Trư ờ ng hợ p b ¹ 0.
Chứ ng minh tư ơ ng tự như trư ờ ng hợ p a ta có:
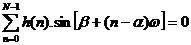 và nghiệ m duy nhấ t củ a nó như sau:
và nghiệ m duy nhấ t củ a nó như sau:
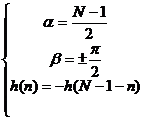
Nhậ n xé t:
- Vớ i mộ t giá trị củ a N, chỉ có duy nhấ t mộ t giá trị a đ ể đ ả m bả o q(w)=b - aw là tuyế n tí nh.
- Vớ i giá trị a nà y đ á p ứ ng xung h(n) = -h(N-1-n) là phả n đ ố i xứ ng.
- Nế u N lẻ thì a là mộ t số nguyê n và tâ m phả n đ ố i xứ ng củ a h(n) là mẫ u thứ (N-1)/2. Ta có bộ lọ c FIR loạ i 3.
- Nế u N chẵ n thì a là mộ t số khô ng nguyê n và tâ m phả n đ ố i xứ ng củ a h(n) nằ m giữ a mẫ u thứ (N-1)/2 và N/2. Ta có bộ lọ c FIR loạ i 4.
Đ ặ c đ iể m quan trọ ng củ a bộ lọ c số FIR loạ i 3 và 4 là tí nh phả n đ ố i xứ ng củ a đ á p ứ ng xung h(n) có rấ t nhiề u ứ ng dụ ng quan trọ ng ta sẽ xé t sau.
Ví dụ: N=6, 7.
3. Tổ ng hợ p bộ lọ c FIR có pha tuyế n tí nh sử dụ ng phư ơ ng phá p cử a sổ.
Việ c nghiê n cứ u cá c phư ơ ng phá p tổ ng hợ p bộ lọ c FIR ở phầ n nà y chú ng ta chỉ dừ ng lạ i ở việ c tí nh toá n cá c hệ số củ a h(n). Cá c hệ số củ a h(n) đ ư ợ c tí nh toá n sao cho toả mã n cá c chỉ tiê u kĩ thuậ t đ ã cho. Bộ lọ c FIR có ư u đ iể m hơ n bộ lọ c IIR là nó luô n ổ n đ ị nh, chú ng ta sẽ xé t cá c bộ lọ c FIR có pha tuyế n tí nh (Đ á p ứ ng xung h(n) đ ố i xứ ng hoặ c phả n đ ố i xứ ng). Cá c hệ thố ng thự c hiệ n đ ư ợ c về mặ t vậ t lý là cá c hệ thố ng nhâ n quả, ổ n đ ị nh.
Có 3 phư ơ ng phá p chí nh đ ể tổ ng hợ p bộ lọ c số FIR là:
- Phư ơ ng phá p cử a sổ.
- Phư ơ ng phá p lấ y mẫ u tầ n số.
- Phư ơ ng phá p lặ p.
Trong chư ơ ng trì nh chú ng ta chỉ tì m hiể u phư ơ ng phá p thứ nhấ t.
a. Nhậ n xé t.
Ta đ ã biế t đ á p ứ ng tầ n số củ a bộ lọ c FIR nhâ n quả bậ c N là:
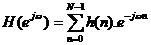 ;
; 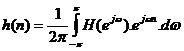
+ Gọ i h(n) là đ á p ứ ng xung củ a bộ lọ c số lí tư ở ng, vì vậ y h(n) có chiề u dà i vô hạ n nê n khô ng thể thự c hiệ n đ ư ợ c. L[h(n) ] = [-¥; +¥ ]
+ h(n) khô ng nhâ n quả, vì thế khô ng thể thự c hiệ n đ ư ợ c.
+ Đ ể cho đ á p ứ ng xung củ a bộ lọ c số lí tư ở ng trở thà nh đ á p ứ ng xung củ a bộ lọ c FIR thì ta phả i là m cho h(n) nhâ n quả và hạ n chế chiề u dà i củ a nó.
+ Đ ể hạ n chế chiề u dà i củ a h(n) ta sẽ sử dụ ng hà m cử a sổ, hay đ ư ợ c gọ i là cử a sổ 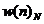 là cử a sổ nhâ n quả có chiề u dà i là N.
là cử a sổ nhâ n quả có chiề u dà i là N.
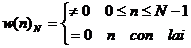
b. Cá c bư ớ c chí nh. Phư ơ ng phá p cử a sổ đ ự oc thự c hiệ n cho bộ lọ c số loạ i 1.
- Bư ớ c 1: Chọ n 4 chỉ tiê u kĩ thuậ t củ a bộ lọ c số thự c tế: wp, ws, d1, d2. Đ ể tì m wc, trong chư ơ ng trì nh cho wc .
- Bư ớ c 2: Chọ n dạ ng cử a sổ 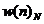 và chiề u dà i cử a sổ N, trong miề n N cử a sổ có tâ m đ ố i xứ ng tạ i
và chiề u dà i cử a sổ N, trong miề n N cử a sổ có tâ m đ ố i xứ ng tạ i 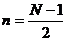 , có pha tuyế n tí nh là
, có pha tuyế n tí nh là 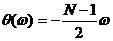 .
.
- Bư ớ c 3: Chọ n loạ i bộ lọ c số lí tư ở ng có đ á p ứ ng xung là h(n), h(n) có tâ m đ ố i xứ ng tạ i 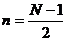 , có pha tuyế n tí nh là
, có pha tuyế n tí nh là 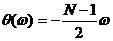 . ( Thay
. ( Thay 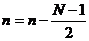 ).
).
- Bư ớ c 4: Nhâ n cử a sổ 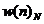 vớ i h(n) thu đ ư ợ c đ á p ứ ng xung thự c tế củ a bộ lọ c FIR loạ i 1.
vớ i h(n) thu đ ư ợ c đ á p ứ ng xung thự c tế củ a bộ lọ c FIR loạ i 1.
hd(n)= 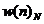 . h(n)
. h(n)
L[ 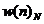 ] = N
] = N
L[h(n) ] =¥
L[hd(n) ]= N
- Bư ớ c 5: Sau khi có hd(n) thử lạ i trong miề n tầ n số xem đ ã đ ạ t chỉ tiê u kĩ thuậ t chư a, nế u chư a đ ạ t là m lạ i vớ i N lớ n hơ n. ( Bư ớ c nà y ta bỏ qua)
c. Mộ t số cử a sổ đ iể n hì nh.
c1. Cử a sổ chữ nhậ t.
Trong miề n n cử a sổ chữ nhậ t đ ư ợ c đ ị nh nghĩ a như sau:
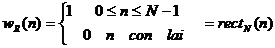

Như vậ y ta thấ y cử a sổ chữ nhậ t chí nh là dã y chữ nhậ t rectN(n).
Như vậ y: 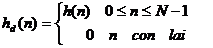
c2. Cử a sổ Hanning và Hamming.
Trong miề n n cử a sổ Hanning và Hamming đ ư ợ c đ ị nh nghĩ a như sau:
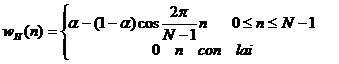
Nế u a = 0. 5 thì ta có cử a sổ Hanning:
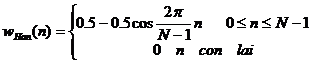
Nế u a = 0. 54 thì ta có cử a sổ Hanning:
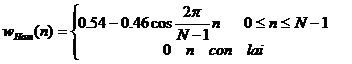
Đ ồ thị củ a cá c cử a sổ nà y như sau:
Ví dụ vớ i N = 9
WHan(n)9và wHam(n)9 đ ố i xứ ng tạ i n = 4
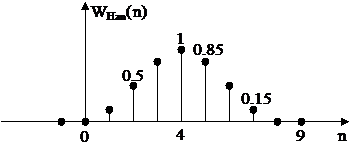 | |||
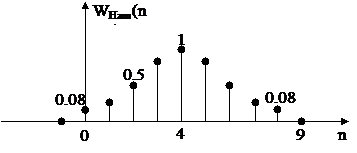 | |||
c3. Cử a sổ tam giá c, Blackman (Giá o trì nh).
Ví dụ: Thiế t kế bộ lọ c thô ng thấ p vớ i cá c chỉ tiê u kĩ thuậ t, wc = p/2, N = 9 dù ng cử a sổ Hanning. Vẽ sơ đ ồ bộ lọ c số:
- Cử a sổ Hanning wHan(n) có N = 9 là cử a sổ nhâ n quả có tâ m đ ố i xứ ng tạ i 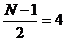 .
.
- Chọ n bộ lọ c số lí tư ở ng thô ng thấ p cũ ng có tâ m đ ố i xứ ng tạ i 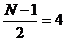 và tầ n số cắ t wc =p/2.
và tầ n số cắ t wc =p/2.
- Vậ y ta có:
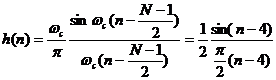
- Do đ ó đ á p ứ ng xung củ a bộ lọ c số thự c tế là:
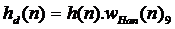
Minh hoạ bằ ng đ ồ thị ta có:
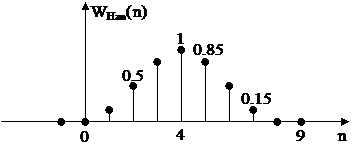 | |||||
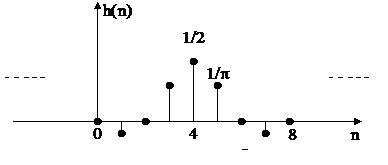 | |||||
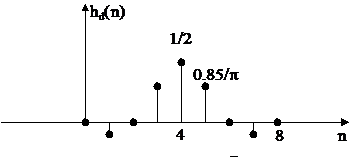 | |||||
Vậ y ta có:
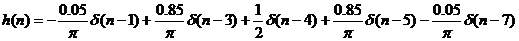
Từ đ â y ta có sơ đ ồ mạ ch như sau:
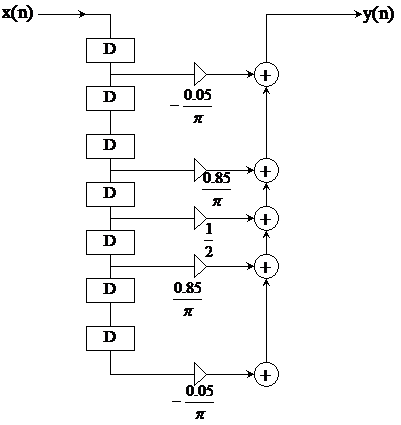 |
§3 Bộ lọ c số IIR
Mở đ ầ u
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|