b./ Bước 2: Nghiệm riêng của phương trình sai phân

Tư ơ ng tự như cá ch tì m nghiệ m củ a phư ơ ng trì nh thuầ n nhấ t, đ ể tì m nghiệ m riê ng củ a phư ơ ng trì nh sai phâ n khi tí n hiệ u và o x(n)¹ 0, ta đ oá n rằ ng nghiệ m củ a phư ơ ng trì nh có mộ t dạ ng nà o đ ó, và thế và o PT-SP-TT-HSH đ ã cho đ ể tì m mộ t nghiệ m riê ng, ký hiệ u y_p(n). Ta thấ y cá ch là m nà y có vẽ mò mẫ m!. Nế u tí n hiệ u và o x(n) đ ư ợ c cho bắ t đ ầ u từ thờ i đ iể m n ³ 0 (nghĩ a là x(n)=0 khi n< 0), thì dạ ng củ a nghiệ m riê ng thư ờ ng đ ư ợ c chọ n là: y_p(n) có dạ ng củ a x(n) từ đ iề u kiệ n đ ầ u

Ví dụ :

Tì m đ á p ứ ng y(n), vớ i n ≥ 0, củ a hệ thố ng đ ư ợ c mô tả bở i pt bậ c hai như sau:

y(n) - 3y(n-1) - 4y(n-2) = x(n) + 2x(n-1) (1. 67)

tí n hiệ u và o là: x(n) = 4ⁿu(n). Hã y xá c đ ị nh nghiệ m riê ng củ a pt(1. 67).

Giả i:

Trong ví dụ 1. 13, ta đ ã xá c đ ị nh nghiệ m củ a phư ơ ng trì nh sai phâ n thuầ n nhấ t cho hệ thố ng nà y, đ ó là pt(1. 63), ta viế t lạ i:

y₀(n) = A₁(-1)ⁿ + A₂(4)ⁿ (1. 68)

Nghiệ m riê ng củ a pt(1. 63) đ ư ợ c giả thiế t có dạ ng hà m mũ: y_p(n) = K(4)ⁿu(n). Tuy nhiê n chú ng ta thấ y dạ ng nghiệ m nà y đ ã đ ư ợ c chứ a trong nghiệ m thuầ n nhấ t (1. 68). Vì vậ y, nghiệ m riê ng nà y là thừ a (thế và o pt(1. 67) ta khô ng xá c đ ị nh đ ư ợ c K). Ta chọ n mộ t dạ ng nghiệ m riê ng khá c đ ộ c lậ p tuyế n tí nh vớ i cá c số hạ ng chứ a trong nghiệ m thuầ n nhấ t. Trong trư ờ ng hợ p nà y, ta xử lý giố ng như trư ờ ng hợ p có nghiệ m ké p trong phư ơ ng trì nh đ ặ c tí nh. Nghĩ a là ta phả i giả thiế t nghiệ m riê ng có dạ ng: y_p(n) = Kn(4)ⁿu(n). Thế và o pt(1. 67):

Kn(4)ⁿu(n) - 3K(n-1)(4)^n-1u(n-1) - 4 K(n-2)(4)^n-2u(n-2) = (4)ⁿu(n) + 2(4)^n-1u(n-1)Đ ể xá c đ ị nh K, ta ư ớ c lư ợ ng phư ơ ng trì nh nà y vớ i mọ i n ≥ 2, nghĩ a là vớ i nhữ ng giá trị củ a n sao cho hà m nhã y bậ c đ ơ n vị trong phư ơ ng trì nh trê n khô ng bị triệ t tiê u. Đ ể đ ơ n giả n về mặ t toá n họ c, ta chọ n n = 2 và tí nh đ ư ợ c K = 6/5. Vậ y:

y_p(n) = (6/5)n(4)ⁿu(n) (1. 69)

c. / Bư ớ c 3: Nghiệ m tổ ng quá t củ a phư ơ ng trì nh sai phâ n:

Tí nh chấ t tuyế n tí nh củ a LCCDE cho phé p ta cộ ng nghiệ m thuầ n nhấ t và nghiệ m riê ng đ ể thu đ ư ợ c nghiệ m tổ ng quá t. Ta có nghiệ m tổ ng quá t là:

y(n) = y₀ (n) + y_p (n) (1. 70)

Vì nghiệ m thuầ n nhấ t y₀(n) chứ a mộ t tậ p cá c hằ ng số bấ t đ ị nh {Ai}, nê n nghiệ m tổ ng quá t cũ ng chứ a cá c hằ ng số bấ t đ ị nh nà y, đ ể xá c đ ị nh cá c hằ ng số nà y, ta phả i có mộ t tậ p cá c đ iề u kiệ n đ ầ u tư ơ ng ứ ng củ a hệ thố ng. Chú ý rằ ng y₀(n) và y_p(n) phả i là đ ộ c lậ p tuyế n tí nh vớ i nhau.

Ví dụ : Tì m đ á p ứ ng y(n), vớ i n ³ 0, củ a hệ thố ng đ ư ợ c mô tả bở i LCCDE bậ c hai trong ví dụ 1. 14 vớ i đ iề u kiệ n đ ầ u là y(-1) = y(-2) = 0.

Giả i:

Trong ví dụ 1. 13 ta đ ã tì m đ ư ợ c nghiệ m thuầ n nhấ t, trong ví dụ 1. 14 ta đ ã tì m đ ư ợ c nghiệ m riê ng. Vậ y nghiệ m tổ ng quá t củ a pt(1. 67) là:

y(n) = y₀(n) + y_P(n) = A₁(-1)n + A₂(4)n + (6/5)n(4)ⁿ, vớ i n≥ 0 (1. 71)

vớ i cá c đ iề u kiệ n đ ầ u là cá c giá trị y(-1) = y(-2) = 0, tư ơ ng tự như trong ví dụ 1. 13, ta tí nh y(0) và y(1) từ cá c pt(1. 67) và (1. 71) và thà nh lậ p đ ư ợ c hệ phâ n trì nh:

A₁ + A₂ = 1

- A₁ + 4 A₂ + 24/5 = 9

suy ra: A ₁ = -1/25 và A₂ = 26/25.

Cuố i cù ng ta thu đ ư ợ c đ á p ứ ng y(n) củ a hệ thố ng vớ i cá c đ iề u kiệ n đ ầ u bằ ng 0, vớ i tí n hiệ u và o là x(n) = (4)nu(n) có dạ ng:

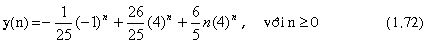
Ví dụ 2: Mộ t hệ thố ng đ ư ợ c mô tả bở i phư ơ ng trì nh sau:

y(n) = 3/4y(n-1) –1/8y(n-2) + x(n) – x(n-1)

a)Tì m đ á p ứ ng ra củ a hệ thố ng vớ i kí ch thí ch là : x(n) = (1/2)ⁿ, y(-1) =y(-2)=0.

b) Tì m đ á p ứ ng xung h(n) củ a hệ thố ng.

Giả i:

a)Ta biế t nghiệ m củ a pt thuầ n nhấ t có dạ ng: y₀(n) = aⁿ, thay và o ta thu đ ư ợ c:

aⁿ - 3/4a^n-1+ 1/8a^n-2 = 0 hay a^{n -2} (a² - 3/4a + 1/8) = 0

và phư ơ ng trì nh đ ặ c trư ng là: (a² - 3/4a + 1/8) = 0

Ta có 2 nghiệ m a₁ = 1/2 và a₂ = 1/4, nghiệ m củ a phư ơ ng trì nh thuầ n nhấ t có dạ ng tổ ng quá t là:

y₀(n) = A₁aⁿ₁ + A₂aⁿ₂ = A₁(1/2)ⁿ + A₂(1/4)ⁿ

Do x(n) = (1/2)ⁿ có dạ ng giố ng như mộ t nghiệ m củ a pt thuầ n nhấ t, vì vậ y ta phả i chọ n y_p(n) có dạ ng sao cho đ ộ c lậ p tuyế n tí nh vớ i x(n).

Chọ n y_p(n) có dạ ng: y_p(n) = B. n(1/2)ⁿ. Thay và o pt ta có:

B. n(1/2)ⁿ = ¾. B. (n-2). (1/2)^n-1 – 1/8B(n-2)(1/2)^n-2 + (1/2)ⁿ – (1/2)^n-1

Chia 2 vế cho (1/2)ⁿ: B. n = 3/2. B. (n-1) – 1/2B. (n-2) –1

Giả i ra ta có: B = - 2, Vậ y nghiệ m củ a phư ơ ng trì nh là:

y(n) = y₀(n) + y_p(n) = A₁(1/2)ⁿ + A₂(1/4)ⁿ - 2. n. (1/2)ⁿ

Dự a và o đ iề u kiệ n đ ầ u ta có thể xá c đ ị nh A₁, A₂:

b) Vớ i x(n) = d(n) thì y(n) = h(n)

Khi n = 0 thì y_p(n) = 0 do đ ó h(n) = y₀(n) = A₁(1/2)ⁿ + A₂(1/4)ⁿ

y(-1) = A₁(1/2)^-1 + A₂(1/4)^-1 – 2. (-1). (1/2)^-1 = 0

y(-2) = A₁(1/2)^-2 + A₂(1/4)^-2 – 2. (-2). (1/2)^-2 = 0

y(0) = 3/4y(-1) – 1/8y(-2) + x(0) - x(-1) = 1 ( Do x(0)= d(0) =1, y(-1)=y(-2)=0)

y(1) = 3/4y(0) – 1/8y(-1) + x(1) - x(0) = ¾ -1 = -1/4

Mặ t khá c, từ pt(1. 63) ta có:

y(0) = A₁ + A₂ = 1

y(1) = 1/2A₁ + 1/4A₂= -1/4

Suy ra: A₁ = -2, A₂ = 3

h(n) = y₀(n) = -2. (1/2)ⁿ + 3(1/2)²ⁿ , vớ i n ³ 0

⇐ Предыдущая 11 12 13 14 151617 18 19 20 Следующая ⇒