BIỂU DIỄN TÍN HIỆU VÀ HỆ THỐNG RỜI RẠC TRÊN MIỀN TẦN SỐ RỜI RẠC

Chư ơ ng 3

BIỂ U DIỄ N TÍ N HIỆ U VÀ HỆ THỐ NG RỜ I RẠ C TRÊ N MIỀ N TẦ N SỐ RỜ I RẠ C

Mở đ ầ u

Trong cá c chư ơ ng trư ớ c chú ng ta đ ã tì m hiể u tí n hiệ u và hệ thố ng rờ i rạ c trê n miề n n, Z, trê n miề n tầ n số chú ng ta đ ã sử dụ ng DTFT đ ể biể u diễ n tí n hiệ u trê n miề n tầ n số liê n tụ c. Trong chư ơ ng nà y chú ng ta sẽ tì m hiể u phé p biế n đ ổ i Fourier rờ i rạ c đ ể biể u diễ n tí n hiệ u trê n miề n tầ n số rờ i rạ c k, vớ i cá c chuỗ i có chiề u dà i hữ u hạ n, cá ch biể u diễ n nà y rấ t có í ch cho cá c má y tí nh số cũ ng như cho việ c thự c hiệ n phầ n cứ ng số.

§1. Chuỗ i Fourier rờ i rạ c củ a tí n hiệ u tuầ n hoà n (DFS)

1. Đ ị nh nghĩ a

Gọ i x_p(n) là dã y tuầ n hoà n có chu kì là N: x_p(n) =x_p(n + N) chuỗ i x_p(n) có thể đ ư ợ c biể u diễ n bằ ng mộ t chuỗ i Fourier rờ i rạ c sau:

(3. 1)

Trong đ ó X_p(k) là dã y tuầ n hoà n chu kì N, bâ y giờ ta đ i tì m X_p(k):

Nhâ n cả 2 vế vớ i 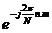ta có:

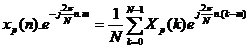
Lấ y tổ ng theo n từ: 0 đ ế n N-1 ta có: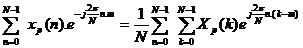

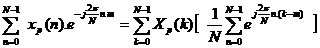
Nhậ n xé t: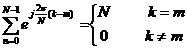

Vậ y vớ i k=m thì ta có:

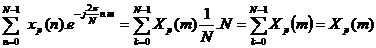
Vậ y ta có: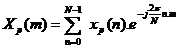

hoặ c ta có: (3. 2)

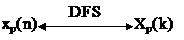Từ (3. 1) và (3. 2) ta có:

2. Cá c tí nh chấ t củ a chuỗ i Fourier rờ i rạ c

a. Tí nh chấ t tuyế n tí nh:

DFS[ x_1p(n) ] = X_1p(k)

DFS[ x_2p(n) ] = X_2p(k)

x_3p(n) = a. x₁(n) + b. x₂(n)

DFS[ x_3p(n) ] = X_3p(k) = a. X_1p(k) + b. X_2p(k)

b. Tí nh chấ t trễ

DFS[ x_1p(n) ] = X_1p(k)

x_2p(n) = x₁(n – n₀)

DFS[ x_2p(n) ] = X_2p(k) =

c. Tổ ng chậ p tuầ n hoà n

DFS[ x_1p(n) ] = X_1p(k)

DFS[ x_2p(n) ] = X_2p(k)

x_3p(n) = x₁(n)(*)x₂(n)

DFS[ x_3p(n) ] = X_3p(k) = X_1p(k). X_2p(k)

§2. Biế n đ ổ i Fourier rờ i rạ c củ a tí n hiệ u khô ng tuầ n hoà n có chiề u dà i hữ u hạ n.

1. Mố i quan hệ giữ a dã y khô ng tuầ n hoà n có chiề u dà i hữ ư hạ n và dã y tuầ n hoà n.

Giả sử có mộ t dã y rờ i rạ c khô ng tuầ n hoà n có chiề u dà i hữ u hạ n là M: x(n)_M và mộ t đ ã y rờ i rạ c tuầ n hoà n chu kì N: x_p(n).

- Nế u M =N thì dã y x(n)_M chí nh là mộ t chu kì củ a dã y x_p(n) ( Vẽ 2 tí n hiệ u )

- Nế u M < N thì ta thấ y dã y có chiề u dà i hữ u hạ n x(n)_M có thể là mộ t chu kì củ a dã y x_p(n) bằ ng cá ch khi chú ng ta coi dã y x(n) là dã y có chiề u dà i là N bằ ng cá ch thê n và o (N-M) mẫ u có giá trị bằ ng 0. Ví dụ ( vẽ hì nh)

Như vậ y từ mộ t dã y khô ng tuầ n hoà n có chiề u dà i hữ u hạ n x(n)_M ta có thể lậ p 1 dã y tuầ n hoà n x_p(n) có chu kì N> = M vớ i mỗ i chu kì củ a dã y tuầ n hoà n x_p(n) sẽ chí nh là dã y x(n)_M.

- Trư ờ ng hợ p M > N ta khô ng thể là m đ ư ợ c như vậ y.

Chú ý: Đ ể nhậ n đ ư ợ c dã y x(n) có chiề u dà i hữ u hạ n chú ng ta có thể sử dụ ng mộ t dã y chữ nhậ t: rect_N(n):

x(n)_M = x_p(n). rect_N(n) =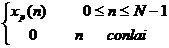

Trê n miề n k thì ta sẽ có: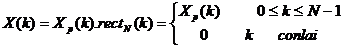

Nhậ n xé t: Chuỗ i Fourier rờ i rạ c củ a dã y tuầ n hoà n đ ư ợ c tí nh trong mộ t chu kì rồ i lấ y tuầ n hoà n từ -∞ đ ế n +∞ vơ is chuu kì là N. Vì vậ y ta có thể lấ y đ ị nh nghĩ a củ a chuỗ i Fourier rờ i rạ c củ a dã y tuầ n hoà n là m đ ị nh nghĩ a cho chuỗ i có chiề u daì hữ u hạ n như ng khô ng đ ư ợ c lấ y tuầ n hoà n, nó chỉ xá c đ ị nh trong miề n giá trị cuả nó, ngoà i miề n giá trị bằ ng 0.

2. Đ ị nh nghĩ a

Cặ p biế n đ ổ i Furier rờ i rạ c (Discrete Fourier Transform )củ a dã y có chiề u dà i hữ u hạ n là N đ ư ợ c đ ị nh nghĩ a như sau:

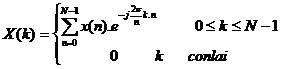
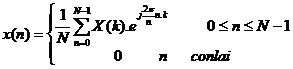
Đ ặ t 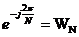ta có:

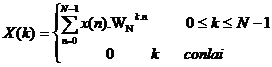
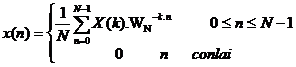
Kí hiệ u: DFT[ x(n) ] = X(k)

IDFT[ X(k) ] = x(n)

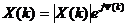
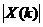gọ i là phổ biê n đ ộ

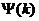gọ i là phổ pha

Ví dụ: Tì m X(k) biế t:

a. x(n) = ∂ (n)

b. x(n) = rect₄(n)

a. Chọ n chiề u dà i củ a dã y là M, vậ y ta có:

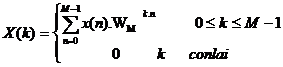
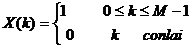
c. Chọ n chiề u dà i củ a dã y là N = 4

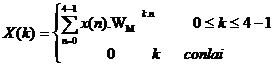
nê n ta có:

X(0) = 1 + (-j) + (-j)² + (-j)³ = 0

Tư ơ ng tự vớ i X(1), X(2), X(3)

3. Cá c tí nh chấ t củ a DFT

a. Tí nh chấ t tuyế n tí nh:

DFT[ x₁(n) ] = X₁(k)

DFT[ x₂(n) ] = X₂(k)

x₃(n) = a. x₁(n) + b. x₂(n)

DFS[ x₃(n) ] = X_3p(k) = a. X₁(k) + b. X₂(k)

b. Tí nh chấ t dị ch vò ng

Dị ch vò ng củ a mộ t dã y x(n) đ ư ợ c đ ị nh nghĩ a như sau:

x(n-n₀)_N. rect_N(n) = x_p(n-n₀). rect_N(n)

Phé p dị ch vò ng củ a mộ t dã y là phé p dị ch trong đ ó cá c mẫ u đ i ra khỏ i đ oạ n [0, N-1] sẽ quay trở lạ i đ ầ u kia.

DFT[ x(n) ] = X(k)

DFT[ x(n-n₀) ] = Y(k) =W^{k. n}X(k)

Cò n nữ a

§ 3. Biế n đ ổ i Fourier nhanh – FFT

I Mở đ ầ u

Trong lĩ nh vự c xử lí số tí n hiệ u, biế n đ ổ i Fourier có vai trò rấ t quan trọ ng, vì vậ y nó tồ n tạ i cá c thuậ t toá n tí nh toá n DFT hiệ u quả hơ n. Từ khi Cooley phá t hiệ n ra thuậ t toá n tì m nhanh biế n đ ổ i DFT, cá c thuậ t toá n ngà y cà ng đ ư ợ c phá t triể n và ứ ng dụ ng nhiề u trong xử lí số tí n hiệ u.

1. Đ ộ phứ c tạ p tí nh toá n củ a DFT

Trong phầ n trư ớ c chú ng ta đ ã tì m hiể u biế n đ ổ i Fourier rờ i rạ c như sau:

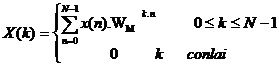(3. 3)

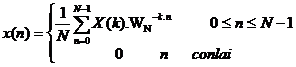(3. 4)

Nhậ n xé t:

- Từ (3. 3) và (3. 4) ta thấ y: X(k) và x(n) chỉ khá c nhau hệ số tỉ lệ (1/N) và dấ u củ a W_N. Như vậ y DFT và IDFT gầ n như là giố ng nhau, do đ ó cá c thuậ t toá n FFT đ ư ợ c sử dụ ng cho cả DFT và IDFT, nghĩ a là cá c thuậ t toá n tí nh nhanh FFT cũ ng á p dụ ng cho IFFT.

- Từ (3. 3) ta thấ y do x(n) có thể có giá trị thự c hoặ c phứ c vì thế đ ể tì m X(k) yê u cầ u thự c hiệ n N phé p nhâ n phứ c và N phé p cộ ng phứ c vớ i 1 giá trị củ a k. Vớ i N giá trị k việ c tí nh DFT- N đ iể m yê u cầ u N² phé p toá n nhâ n phứ c và N² phé p toá n cộ ng phứ c. Do đ ó khi N lớ n số lư ợ ng phé p toá n sẽ rấ t lớ n vì vậ y cầ n thuậ t toá n tì m X(k) (x(n)) hiệ u quả hơ n.

- Giả i thuậ t cơ bả n củ a thuậ t toá n tí nh nhanh FFT là việ c phâ n giã DFT-N đ iể m thà nh cá c DFT-N_i nhỏ hơ n (N_i< N) khi đ ó số lư ợ ng phé p toá n sẽ giả m đ i rấ t nhiề u (cỡ i. N_i²).

- Cá c thuậ t toá n tí nh nhanh biế n đ ổ i Fourier đ ề u dự a và o tí nh chấ t củ a W_N.

2. Cá c tí nh chấ t củ a W_N.

a. Tí nh tuầ n hoà n

W_N^{k. n} = W_N^{(k’. n’ + iN)} =W_N^{k’. n’}

Do n Î [0, N-1]

k Î [0, N-1]

nê n k. n Î [0, (N-1). (N-1) ] và k. n = k’. n’ + iN

Ví dụ: Cho DFT – N=8 hã y dù ng tí nh chấ t tuầ n hoà n đ ể tí nh X(7)

Từ (3. 3) Ta có:

X(7) = x(0). W₈^{7. 0} + x(1). W₈^{7. 1}+ x(2). W₈^{7. 2}+ x(3). W₈^{7. 3} + x(4). W₈^{7. 4}+ x(5). W₈^{7. 5}+ x(6). W₈^{7. 6}+ x(7). W₈^{7. 7}

X(7) = x(0). W₈⁰ + x(1). W₈⁷+ x(2). W₈¹⁴+ x(3). W₈²¹ + x(4). W₈²⁸+ x(5). W₈³⁵+ x(6). W₈⁴²+ x(7). W₈⁴⁹

Do tí nh chấ t tuầ n hoà n củ a W_Nnê n ta có:

W⁰₈= W₈⁰

W⁷₈= W₈⁷

W¹⁴₈= W₈^{(6+1. 8)} = W⁶₈ W⁴²₈= W₈^{(2+5. 8)} = W²₈

W²¹₈= W₈^{(5+2. 8)} = W⁵₈ W⁴⁹₈= W₈^{(1+6. 8)} = W¹₈

W²⁸₈= W₈^{(4+3. 8)} = W⁴₈

W³⁵₈= W₈^{(3+4. 8)} = W³₈

Vậ y: X(7) = X(7) = x(0). W₈⁰ + x(1). W₈⁷+ x(2). W₈⁶+ x(3). W₈⁵ + x(4). W₈⁴+ x(5). W₈³+ x(6). W₈²+ x(7). W₈¹

b. Tí nh chấ t đ ố i xứ ng.

W^k’n’_N = W_N^{(N-k’’n’’)} = W_N^N. W_N^{-k’’. n’’} = W_N^{-k”. n”} do W^N_N= 1

Ví dụ: W⁷₈= W₈^(8-1)= W^-1₈^......

Dự a và o cá c tí nh chấ t nà y ngư ờ i ta có cá c giả i thuậ t phâ n chia theo thờ i gian và phâ n chia theo tầ n số, trong chư ơ ng trì nh chú ng ta chỉ tì m hiể u giả i thuậ t phâ n chia theo thờ i gian vớ i N = 2^m cò n cá c trư ờ ng hợ p khá c sv tự ngiê n cứ u!

3. Thuậ t toá n FFT cơ số 2 phâ n chia theo thờ i gian ( FFT – R₂)

a. Trư ờ ng hợ p N=2^m

Nộ i dung củ a giả i thuậ t nà y là phâ n chia dã y x(n) thà nh cá c dã y có chiề u dà i nhỏ hơ n và tì m X(k) từ cá c DFT củ a chuỗ i đ ã đ ư ợ c chia nhỏ.

Thuậ t toá n:

- Gọ i x(n) là dã y có chiề u dà i là N = 2^m, giả sử x(n) đ ư ợ c chia thà nh 2 dã y con x(2n) và x(2n+1), mỗ i dã y có chiề u dà i là N/2

+ Dã y x(2n) là dã y chứ a cá c mẫ u chẵ n củ a x(n).

+ Dã y x(2n+1) là dã y chứ a cá c mẫ u chẵ n củ a x(n).

Ví dụ:

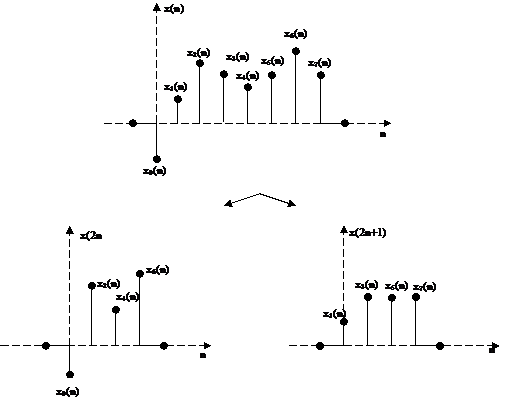Do:

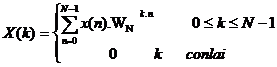nê n vớ i 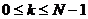ta có:

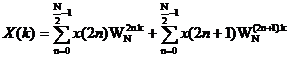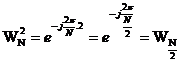do nê n

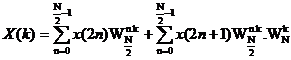do W^k_N khô ng phụ thuộ c và o n nê n:

Đ ặ t là DFT – N/2 đ iể m chẵ n củ a x(n)

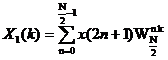là DFT – N/2 đ iể m lẻ củ a x(n)

ta có: X(k) = X₀(k) + W_N^k. X₁(k) (3. 5)

Nhậ n xé t: Cá c phé p toá n tì m X₀(k) và X₁(k) chỉ thự c hiệ n trong khoả ng từ: 0 đ ế n( N/2 –1). Do vậ y thự c chấ t ta đ ã phâ n chia DFT – N đ iể m thà nh 2 DFT – N/2 đ iể m. X₀(k) và X₁(k) tuầ n hoà n chu kì N/2.

Ví dụ:

Thự c hiệ n DFT – N=8

Từ (3. 5) ta có: X(k) = X₀(k) + W_N^k. X₁(k)

Suy ra: X(0) = X₀(0) + W₈⁰. X₁(0) X(4) = X₀(4) + W₈⁴. X₁(4)

X(1) = X₀(1) + W₈¹. X₁(1) X(5) = X₀(5) + W₈⁵. X₁(5)

X(2) = X₀(2) + W₈². X₁(2) X(6) = X₀(6) + W₈⁶. X₁(6)

X(3) = X₀(3) + W₈³. X₁(3) X(7) = X₀(7) + W₈⁷. X₁(7)

Do X₀(k) và X₁(k) tuầ n hoà n chu kì N/2 = 8/2 =4 do đ ó:

X(0) = X₀(0) + W₈⁰. X₁(0) X(4) = X₀(0) + W₈⁴. X₁(0)

X(1) = X₀(1) + W₈¹. X₁(1) X(5) = X₀(1) + W₈⁵. X₁(1)

X(2) = X₀(2) + W₈². X₁(2) X(6) = X₀(2) + W₈⁶. X₁(2)

X(3) = X₀(3) + W₈³. X₁(3) X(7) = X₀(3) + W₈⁷. X₁(3)

Từ đ â y ta có thể xâ y dự ng lư u đ ồ sau:

Quy tắ c xâ y dự ng lư u đ ồ:

- Giá trị củ a mộ t nú t bằ ng tổ ng cá c nhá nh đ i và o nú t đ ó.

- Giá trị củ a mộ t nhá nh bằ ng giá trị nú t xuấ t phá t nhâ n vớ i hệ số truyề n củ a nhá nh.

- Hệ số truyề n củ a nhá nh ghi ở mũ i tê n, nế u khô ng ghi thì hệ số truyề n bằ ng 1.

Lư u đ ồ DFT –N=8 sau 1 lầ n phâ n chia. Vẽ hì nh sau

- Tiế p tụ c ta lạ i chia 2 dã y x(2n) và x(2n+1) mỗ i dã y thà nh 2 dã y con giố ng như trê n. Giả i thuậ t tiế p tụ c sau (m-1) lầ n chia thì chỉ cò n là DFT – 2 khi đ ó cá c hệ số truyề n W^k_N chỉ mang 2 giá trị là: W⁰₂ = 1 và W¹₂ = -1. Ta sẽ dừ ng phé p chia tạ i đ â y.

Ví dụ: N=8 sau 2 lầ n phâ n chia ta có:

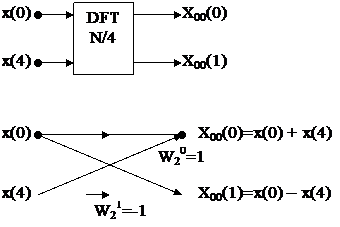Và ta có:

Đ â y đ ư ợ c gọ i là dạ ng cá nh bư ớ m củ a FFT –R₂. Kế t hợ p lạ i ta có lư u đ ồ sau: N=8

· Hiệ u quả thuậ t toá n: Do N=2^m nê n suy ra có m ltầ ng tí nh toá n, mỗ i tầ ng gồ m N/2 phé p nhâ n số phứ c vớ i W^k_N và N phé p cộ ng số phứ c. Vậ y ta cầ n có (1/2). N. m phé p nhâ n phứ c và (1/2)N. m phé p cộ ng. Số lư ợ ng phé p toá n giả m đ i đ á ng kể.

· Ví dụ: N=8 sử dụ ng cô ng thứ c củ a DFT thì cỡ: N²=64

Sử dụ ng FFT-R₂ số lư ợ ng phé p toá n cỡ: N. m = 8. 3=24.

· Cả i thiệ n thuậ t toá n:

Xé t giữ a 2 tầ ng củ a thuậ t toá n liề n kề : i và i+1

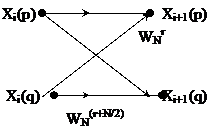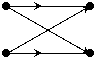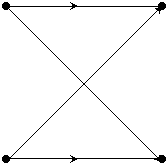Theo hì nh vẽ ta thấ y giữ a 2 tầ ng i và (i+1) ta có:

X_i+1(p) = X_i(p) + W_N^r. X_i(q)

X_i+1(q) = X_i(p) + W_N^(r+N/2). X_i(q)

Ta lạ i thấ y: 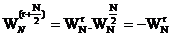vậ y ta có:

X_i+1(p) = X_i(p) + W_N^r. X_i(q)

X_i+1(q) = X_i(p) - W_N^r. X_i(q)\

Sơ đ ồ đ ư ợ c vẽ lạ i:

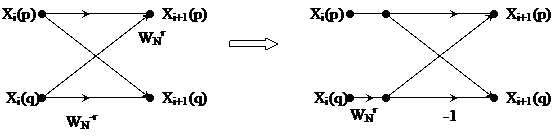Vậ y vớ i mộ t phé p nhâ n W_N^r. X_i(q) ta có thể tí nh 2 giá trị X_i+1(p) và X_i+1(q). Do đ ó số lư ợ ng phé p nhâ n sẽ giả m đ i 2 lầ n cò n số lư ợ ng phé p cộ ng vẫ n giữ nguyê n. Vậ y đ ể tí nh đ ư ợ c X(k)_N thì cầ n:

N. log₂N phé p cộ ng phứ c

(½ )N. log₂N phé p nhâ n phứ c.

Vậ y ta có thể xâ y dự ng lư u đ ồ thuậ t toá n FFT – R₂ ( ví dụ N=8 ) như sau:

Chú ý: Khi thự c hiệ n trê n má y tí nh hoặ c thiế t kế dã y và o x(n) thư ờ ng đ ư ợ c xắ p xế p theo mã nhị phâ n đ ả o cò n X(k) đ ư ợ c xắ p xế p theo mã nhị phâ n thư ờ ng.

x(n)	Mã nhị phâ n đ ả o	Mã nhị phâ n thư ờ ng	X(k)
x(0)			X(0)
x(4)			X(1)
x(2)			X(2)
x(6)			X(3)
x(1)			X(4)
x(5)			X(5)
x(3)			X(6)
x(7)			X(7)
	Trụ c đ ả o	Trụ c đ ả o

b. Trư ờ ng hợ p: N=B^a; N=B₁. B₂(SV đ ọ c giá o trì nh)

4. Thuậ t toá n phâ n chia theo tầ n số ( Giố ng phâ n chia theo thờ i gian) Tự nghiê n cứ u.

5. Tí nh tổ ng chậ p nhanh sử dụ ng FFT

y(n) =x(n)*h(n)

⇐ Предыдущая 11 12 13 14 15 16 17 181920 Следующая ⇒