
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
5.3. Thực hiện hệ FIR và IIR
5. 3. Thự c hiệ n hệ FIR và IIR
Hệ FIR:
Đ ố i vớ i hệ thố ng FIR khô ng đ ệ qui, vớ i phư ơ ng trì nh sai phâ n biể u diễ n hệ thố ng là:
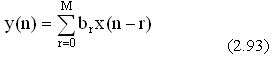
Ta có sơ đ ồ như sau:
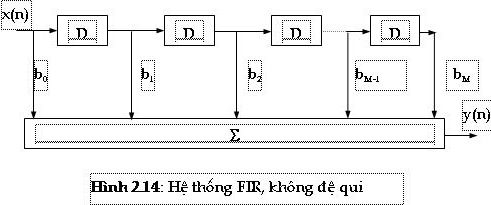
Trong thự c tế, đ ố i vớ i cá c mạ ch đ ệ qui, í t khi ngư ờ i ta thự c hiệ n cả mộ t sơ đ ồ có bậ c N > 2, vì khi đ ó mạ ch dễ mấ t tí nh ổ n đ ị nh do sai số. Mặ t khá c, thiế t kế cá c khâ u bậ c 2 có phầ n thuậ n lợ i hơ n. Vì vậ y, ngư ờ i ta chia hệ thố ng ra thà nh nhiề u mạ ch con có bậ c lớ n nhấ t là 2 mắ c liê n tiế p hoặ c song song vớ i nhau.
Hệ IIR
Pt củ a hệ IIR đ ư ợ c viế t lạ i dư ớ i dạ ng cô ng thứ c truy hồ i:
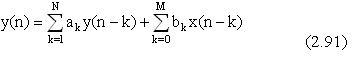
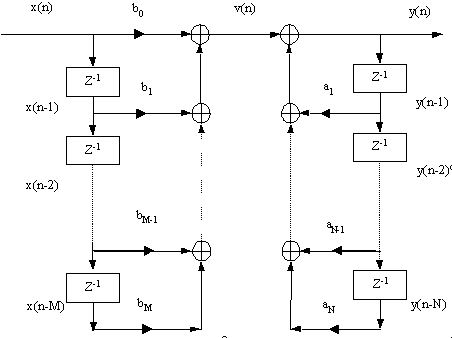
Sơ đ ồ khố i hì nh 2. 11 biể u diễ n bằ ng hì nh ả nh củ a pt(2. 91)
Chư ơ ng II
BIỂ U DIỄ N TÍ N HIỆ U
VÀ HỆ THỐ NG RỜ I RẠ C TRONG MIỀ N Z
| Mờ đ ầ u |
Chư ơ ng 1 đ ã trì nh bà y cá ch tí nh đ á p ứ ng củ a mộ t hệ thố ng trự c tiế p từ đ á p ứ ng xung củ a nó, bằ ng cá ch tí nh tổ ng chậ p củ a kí ch thí ch vớ i đ á p ứ ng xung. Cá ch tí nh tổ ng chậ p trự c tiế p dự a và o cô ng thứ c đ ị nh nghĩ a như đ ã là m tố n rấ t nhiề u thờ i gian và cô ng sứ c. Hơ n nữ a, trong thự c tế số mẫ u khá c khô ng củ a kí ch thí ch và đ á p ứ ng xung là rấ t nhiề u nê n ta khô ng thể ‘tí nh bằ ng tay’. Tuy nhiê n, phư ơ ng phá p tí nh tổ ng chậ p bằ ng đ ồ thị như đ ã trì nh bà y cho ta mộ t thuậ t toá n củ a chư ơ ng trì nh tí nh tổ ng chậ p bằ ng má y tí nh. Việ c giả i phư ơ ng trì nh sai phâ n tuyế n tí nh hệ số hằ ng bằ ng phư ơ ng phá p đ ệ qui cũ ng chỉ có ý nghĩ a khi sử dụ ng má y tí nh.
Kỹ thuậ t biế n đ ổ i là mộ t cô ng cụ hữ u hiệ u đ ể phâ n tí ch hệ thố ng LTI. Biế n đ ổ i Z đ ố i vớ i tí n hiệ u rờ i rạ c có vai trò tư ơ ng tự như biế n đ ổ i Laplace đ ố i vớ i tí n hiệ u liê n tụ c, và chú ng có quan hệ giố ng nhau vớ i biế n đ ổ i Fourier. Tổ ng chậ p củ a hai dã y trong miề n thờ i gian sẽ biế n thà nh tí ch củ a hai biế n đ ổ i Z tư ơ ng ứ ng trong miề n biế n phứ c z. Tí nh chấ t nà y sẽ là m đ ơ n giả n hó a việ c tí nh đ á p ứ ng củ a hệ thố ng vớ i cá c tí n hiệ u và o khá c nhau. Phư ơ ng trì nh sai phâ n tuyế n tí nh hệ số hằ ng cũ ng đ ư ợ c giả i mộ t cá ch dễ dà ng hơ n khi dù ng cô ng cụ biế n đ ổ i Z.
Như ta sẽ thấ y trong cá c chư ơ ng sau, biế n đ ổ i Fourier giữ a vai trò chì a khó a trong trong việ c biể u diễ n và phâ n tí ch cá c hệ thố ng rờ i rạ c. Tuy nhiê n, trong mộ t số trư ờ ng hợ p cầ n phả i sử dụ ng dạ ng tổ ng quá t hó a củ a biế n đ ổ i Fourier, đ ó là biế n đ ổ i Z.
1. Biế n đ ổ i z
Biế n đ ổ i Z trự c tiế p
Đ ị nh nghĩ a: Biế n đ ổ i Z củ a tí n hiệ u rờ i rạ c x(n) đ ư ợ c đ ị nh nghĩ a như sau:
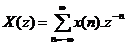 (2. 1)
(2. 1)
Trong đ ó z là biế n phứ c và đ ư ợ c biể u diễ n như sau:
X(z) = ZT[x(n)]
Do chuỗ i biế n đ ổ i là vô hạ n nê n chỉ tồ n tạ i mộ t số giá trị củ a Z đ ể X(z) hộ i tụ. Tậ p hợ p cá c giá trị củ a z đ ể X(z) hộ i tụ gọ i là miề n hộ i tụ củ a X(z) kí hiệ u là ROC[ X(z) ]
VD1: Xá c đ ị nh biế n đ ổ i z củ a tí n hiệ u rờ i rạ c sau:
a/ x(n) = {1, 2, 5, 7, 0, 1 }
b/ x(n) = δ (n)
c/ x(n) = δ (n - k), k> 0
d/ x(n) = δ (n + k), k> 0
Như vậ y vớ i tí n hiệ u hữ ư hạ n thì ROC là toà n bộ mặ t phẳ ng z và có thể trừ cá c giá trị z = 0 và z = ∞
VD2: Xá c đ ị nh biế n đ ổ i z củ a cá c tí n hiệ u rờ i rạ c sau:
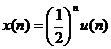
Suy ra 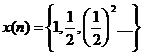
Á p dụ ng cô ng thứ c 3. 1 ta có:
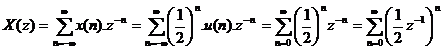
X(z) hộ i tụ khi 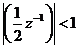 khi đ ó ta có:
khi đ ó ta có: 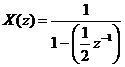
Vậ y ROC [X(z)]: 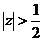
· Mặ t phẳ ng z
Do z là biế n phứ c nê n: z = Re[z] + j Im[z], mặ t phẳ ng z đ ư ợ c tạ o bở i trụ c tung Im[z] và trụ c hoà nh Re[z]
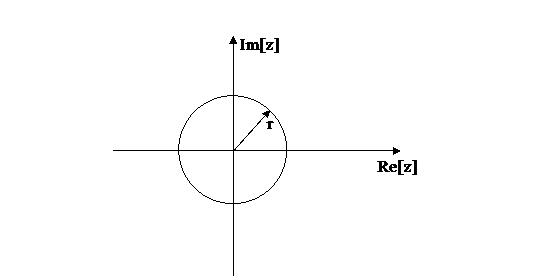
Chú ý: z là biế n phứ c nê n ta có thể biể u diễ n như sau:
z = rejθ
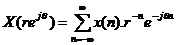 , Nế u r =1 thì
, Nế u r =1 thì 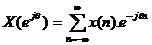 có nghĩ a là phé p biế n đ ổ i z lấ y trê n vò ng trò n đ ơ n vị sẽ trở thà nh biế n đ ổ i Fourier trê n miề n tầ n số.
có nghĩ a là phé p biế n đ ổ i z lấ y trê n vò ng trò n đ ơ n vị sẽ trở thà nh biế n đ ổ i Fourier trê n miề n tầ n số.
· Á p dụ ng tiê u chuẩ n Cauchy đ ể xá c đ ị nh miề n hộ i tụ củ a biế n đ ổ i z.
- Tiê u chuẩ n Cauchy: Mộ t chuỗ i có dạ ng 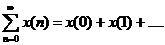 hộ i tụ nế u đ iề u kiệ n sau thoả mã n:
hộ i tụ nế u đ iề u kiệ n sau thoả mã n: 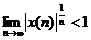
- Á p dụ ng vớ i biế n đ ổ i z ta có: 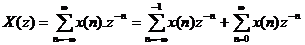
Đ ặ t X(z) = X1(z) + X2(z)
Trong đ ó: X1(z) = 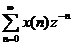
X2(z) = 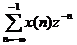
Á p dụ ng tiê u chuẩ n Cauchy cho X1(z) ta có:
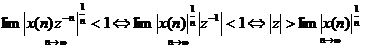 đ ặ t Rx-=
đ ặ t Rx-= 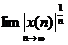 vậ y:
vậ y:
Vớ i 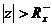 thì X1(z) hộ i tụ. Tứ c là miề n hộ i tụ củ a X1(z) nằ m ngoà vò ng trò n bá n kí nh R-x tâ m gố c toạ đ ộ trê n mặ t phẳ ng z. Đ ậ y cũ ng là miề n hộ i tụ củ a dã y nhâ n quả có chiề u dà i vô hạ n.
thì X1(z) hộ i tụ. Tứ c là miề n hộ i tụ củ a X1(z) nằ m ngoà vò ng trò n bá n kí nh R-x tâ m gố c toạ đ ộ trê n mặ t phẳ ng z. Đ ậ y cũ ng là miề n hộ i tụ củ a dã y nhâ n quả có chiề u dà i vô hạ n.
Á p dụ ng tiê u chuẩ n Cauchy vớ i X2(z). tư ơ ng tự như vớ i X1(z) ta cũ ng có miề n hộ i tụ củ a X2(z) là: 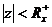 trong đ ó : Rx+=
trong đ ó : Rx+= 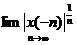 , nghĩ a là miề n hộ i tụ củ a X2(z) là miề n nằ m trong đ ư ờ ng trò n bá n kí nh R+x tâ m gố c toạ đ oọ trê n mặ t phẳ ng z, đ â y cũ ng là miề n hộ i tụ củ a dã y phả n nhâ n quả có chiề u dà i vô hạ n.
, nghĩ a là miề n hộ i tụ củ a X2(z) là miề n nằ m trong đ ư ờ ng trò n bá n kí nh R+x tâ m gố c toạ đ oọ trê n mặ t phẳ ng z, đ â y cũ ng là miề n hộ i tụ củ a dã y phả n nhâ n quả có chiề u dà i vô hạ n.
Kế t luậ n vậ y miề n hộ i tụ củ a X(z) là: X1(z)∩ X2(z).
VD 3: Xá c đ ị nh biế n đ ổ i z củ a tí n hiệ u x(n) = anu(n)
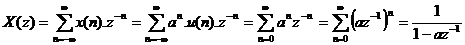
nế u 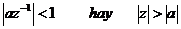
Vậ y 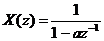 , ROC [X(z)]:
, ROC [X(z)]: 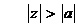 (3)
(3)
VD4: Xá c đ ị nh biế n đ ổ i z củ a tí n hiệ u x(n) = - anu(-n-1)
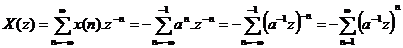
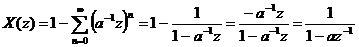
Vớ i 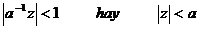
Vậ y 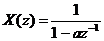 , ROC [X(z)]:
, ROC [X(z)]: 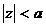 (4)
(4)
Từ (3) và (4) ta thấ y: Hai tí n hiệ u khá c nhau có cù ng biế n đ ổ i z như ng ROC khá c nhau. Do đ ó, tí n hiệ u rờ i rạ c x(n) xá c đ ị nh duy nhấ t bằ ng biế n đ ổ i z và ROC củ a nó.
Cá c tí nh châ t củ a biế n đ ổ i z.
a. Tí nh chấ t tuyế n tí nh
Nế u:
X1(z) = ZT[x1(n)], ROC[X1(z)]
X2(z) = ZT[x2(n)], ROC[X2(z)]
x3(n) = ax1(n) + bx2(n) trong đ ó a, b là cá c hằ ng số thì:
ZT[x3(n)] = X3(z) = a. X1(z) + b. X2(z),
ROC[X3(z)] = ROC[X1(z)] ∩ ROC[X2(z)]
Ví dụ : x1(n) = 2nu(n), x2(n) = 3nu(n)
b. Tí nh chấ t dị ch thờ i gian
Nế u:
X(z) = ZT[x(n)], ROC[X(z)]
thì ZT [x(n-k)] = z-kX(z)
Miề n hộ i tụ:
+ Nế u k > 0 thì ROC: là ROC[X(z)]/0
+ Nế u k< 0 thì ROC là ROC[X(z)]/∞
c. Đ ị nh lí giá trị đ ầ u
Biế n đ ỏ i z củ a dã y nhâ n quả x(n) đ ư ợ c đ ị nh nghĩ a như sau:
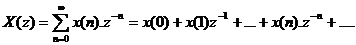
Khi z→ ∞ thì lim X(z) → x(0)
Ví dụ: Hã y cá c đ ị nh giá trị đ ầ u củ a dã y sau:
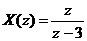 , ROC:
, ROC: 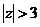
x(0) = 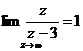
d. Tí ch chậ p trê n miề n z.
Nế u:
X1(z) = ZT[x1(n)], ROC[X1(z)]
X2(z) = ZT[x2(n)], ROC[X2(z)]
x3(n) = x1(n) * x2(n) thì:
ZT[x3(n)] = X3(z) = X1(z). X2(z),
ROC[X3(z)] = ROC[X1(z)] ∩ ROC[X2(z)], Miề n hộ i tụ củ a X3(z) có thể rộ ng hơ n miề n hộ i tụ củ a X1(z) và X2(z).
Ví dụ : x1(n) = 2nu(n), x2(n) = 3nu(n)
e. Nhâ n vớ i hà m mũ
Giả sử có dã y x(n) có ZT[x(n)] =X(z), ROC: 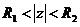 thì dã y:
thì dã y:
y(n) = anx(n) có ZT[y(n)] = Y(z) = 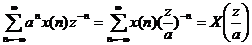
ROC: 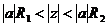
Ví dụ: cho dã y x(n) = 2nu(n) xá c đ ị nh X(z), ROC.
Trư ớ c tiê n ta tì m biế n đ ổ i z củ a dã y u(n):
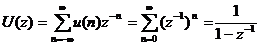 vớ i ROC:
vớ i ROC: 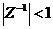 hay
hay 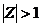
Vậ y 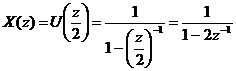 vớ i ROC:
vớ i ROC: 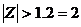
Biế n đ ổ i z hữ u tỷ.
Giả sử X(z) là hà m hữ u tỷ: 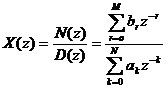
a. Cá c khá i niệ m cự c và khô ng.
+ Đ iể m cự c củ a X(z) là cá c giá trị z tạ i đ ó X(z) = ∞, kí hiệ u là zck, khi đ ó D(zck) = 0
+ Đ iể m khô ng củ a X(z) là cá c đ iể m tạ i đ ó X(z) = 0, kí hiệ u là zor, khi đ ó N(zor) = 0
b. Biể u diễ n X(z) dư ớ i dạ ng cự c và khô ng
Giả sử N(z) là đ a thứ c bậ c M củ a z khi đ ó:
N(z) = bM(z- zo1) (z- zo2) (z- zo3).... (z- zoM)= 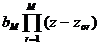
Giả sử D(z) là đ a thứ c bậ c N củ a z khi đ ó:
D(z) = aN(z- zc1) (z- zc2) (z- zc3).... (z- zcN)= 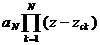
Khi đ ó X(z) đ ư ợ c viế t lạ i như sau:
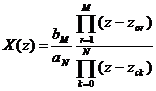 hay ta có thể viế t dư ớ i dả ng hà m củ a z-1 như sau:
hay ta có thể viế t dư ớ i dả ng hà m củ a z-1 như sau:
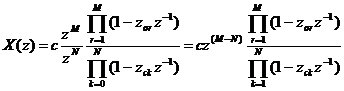
Vớ i c = bM/aN X(z) có M đ iể m khô ng và N đ iể m cự c. Đ ể biể u diễ n trê n đ ồ thị cá c đ iể m cự c đ ư ợ c đ á nh dấ u bằ ng (x) và cá c đ iể m khô ng đ ư ợ c đ á nh dấ u bằ ng (o)
Ví dụ: Xá c đ ị nh biế n đ ổ i z củ a tí n hiệ u đ ư ợ c cho bở i giả n đ ồ cự c và khô ng như sau:
Vẽ hì nh
2. Biế n đ ổ i z ngư ợ c
Đ ị nh lí Cauchy
Đ ị nh lí Cauchy là mộ t đ ị nh lí quan trọ ng trong lí thuyế t biế n số phứ c, nó là cơ sở đ ể chú ng ta xâ y dự ng cô ng thứ c củ a biế n đ ổ i z ngư ợ c.
Đ ị nh lí Cauchy đ ư ợ c phá t biể u như sau:
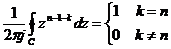
Trong đ ó C là mộ t đ ư ờ ng cong kí n bấ t kì.
2. 2 Biế n đ ổ i z ngư ợ c
Từ biể u thứ c 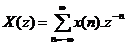 ta có:
ta có:
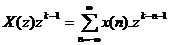 lấ y tí ch phâ n trê n miề n hộ i tụ ROC củ a nó ta có :
lấ y tí ch phâ n trê n miề n hộ i tụ ROC củ a nó ta có :
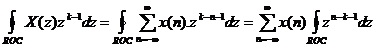
Á p dụ ng đ ị nh lí Cauchy ta có:
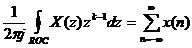 vớ i k = n
vớ i k = n
Hay 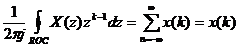
vậ y: 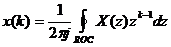 hoặ c ta có thể viế t:
hoặ c ta có thể viế t:
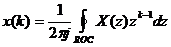 (2. 2)
(2. 2)
Biể u thứ c (2. 2) đ ư ợ c gọ i là biể u thứ c củ a biế n đ ổ i Z ngư ợ c ( IZT – Invert Z Transform ).
Từ biể u thứ c (2. 2) trong thự c tế có nhiề u phư ơ ng phá p tì m biế n đ ổ i z ngư ợ c thuậ n tiệ n hơ n thự c hiệ n biể u thứ c (2. 2).
2. 3 Cá c phư ơ ng phá p tì m biế n đ ổ i z ngư ợ c
a. / Phư ơ ng phá p thặ ng dư ( Giá o trì nh )
Nộ i dung củ a phư ơ ng phá p là dù ng lí thuyế t thặ ng dư đ ể thự c hiệ n biể u thứ c (2. 2).
b. / Phư ơ ng phá p khai triể n thà nh chuỗ i luỹ thừ a.
Do X(z) là hà m củ a mộ t chuỗ i luỹ thừ a vì vậ y trê n miề n hộ i tụ củ a nó ta có thể khai triể n X(z) dư ớ i dạ ng:
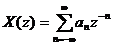 mà theo đ ị nh nghĩ a củ a biế n đ ổ i z ta có:
mà theo đ ị nh nghĩ a củ a biế n đ ổ i z ta có: 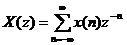
Do vậ y x(n) = an vớ i -∞ < n < ∞
Có nghĩ a là cá c hệ số củ a z-n chí nh là cá c giá trị củ a x(n).
VD1: Hã y xá c đ ị nh x(n) biế t: X(z) = z +2 + 2. z-1 + 3. z-2 – 4. z-4
Từ đ ị nh nghĩ a củ a biế n đ ổ i z ta có: x(n) ={1, 2, 2, 3, 0, -4} hay ta có thể viế t:
x(n) = δ (n+1) + 2δ (n) + 2δ (n-1) +3δ (n-2) - 4δ (n-4)
VD2: Cho 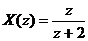 hã y xá c đ ị nh x(n) vớ i:
hã y xá c đ ị nh x(n) vớ i:
a. ROC[X(z)] là: 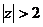
b. ROC[X(z)] là: 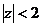
a. Đ â y là tí n hiệ u nhâ n quả có chiề u dai vô hạ n vậ y ta có:
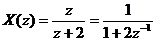 ta thự c hiệ n phé p chia tử số cho mẫ u số ta sẽ có:
ta thự c hiệ n phé p chia tử số cho mẫ u số ta sẽ có:
X(z) = 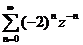 suy ra: x(n) = (-2)nu(n)
suy ra: x(n) = (-2)nu(n)
b. Đ â y là tí n hiệ u phả n nhâ n quả có chiề u dà i vô hạ n. Ta có: 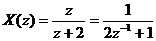 tư ơ ng tự như trê n ta
tư ơ ng tự như trê n ta
cuố i cù ng ta có:
 X(z) =
X(z) = 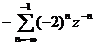 vậ y x(n) = -(-2)nu(-n-1)
vậ y x(n) = -(-2)nu(-n-1)
Nhậ n xé t: Từ ví dụ trê n ta có nế u X(z) có dạ ng: 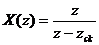 thì ta có biế n đ ổ i z ngư ợ c IZT[X(z)]= x(n) =
thì ta có biế n đ ổ i z ngư ợ c IZT[X(z)]= x(n) = 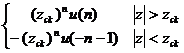
c. / Biế n đ ổ i z ngư ợ c vớ i X(z) là hà m hữ u tỷ.
Giả sử X(z) là hà m hữ u tỷ vớ i a0 = 1
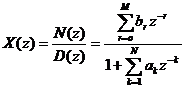
Nế u M ≥ N thì ta có thể biể u diễ n X(z) như sau:
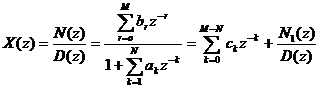 đ a thứ c
đ a thứ c 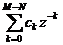 dễ dà ng xá c đ ị nh đ ư ợ c biế n đ ổ i z ngư ợ c củ a nó nhờ tí nh chấ t dị ch trễ thờ i gian.
dễ dà ng xá c đ ị nh đ ư ợ c biế n đ ổ i z ngư ợ c củ a nó nhờ tí nh chấ t dị ch trễ thờ i gian.
Cò n đ a thứ c N1(z)/D(z) là đ a thú c có bậ c củ a D(z) lớ n hơ n bậ c củ a N1(z).
Bâ y giờ ta xé t trư ờ ng hợ p M< N.
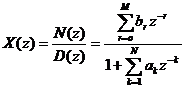 , M< N và aN ≠ 0 ta sẽ khai triể n đ a thứ c nà y thà nh cá c phâ n thứ c tố i giả n.
, M< N và aN ≠ 0 ta sẽ khai triể n đ a thứ c nà y thà nh cá c phâ n thứ c tố i giả n.
- Nế u X(z) chỉ có cá c cự c đ ơ n thì ta có:
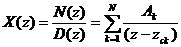 trong đ ó zck là cá c cự c củ a X(z), Ak đ ư ợ c xá c đ ị nh như sau:
trong đ ó zck là cá c cự c củ a X(z), Ak đ ư ợ c xá c đ ị nh như sau: 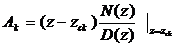
- Nế u X(z) có 1 cự c bộ i, giả sử cự c bộ i bậ c s là zci cá c cự c cò n lạ i lkà cá c cự c đ ơ n thì ta có:
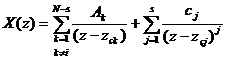 trong đ ó :
trong đ ó :
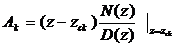 ;
; 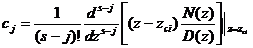
- Nế u X(z) có nhiề u hơ n mộ t cự c bộ i thì ta là m tư ơ ng như trê n.
Sau khi khai triể n xong X(z) ta sẽ tì m IZT[X(z)] củ a cá c phâ n thứ c tố i giả n bở i cá c cô ng thứ c sau:
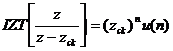 (dã y nhâ n quả )
(dã y nhâ n quả )
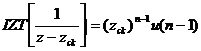
Tổ ng quá t ta có: 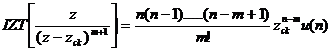 vớ i dã y nhâ n quả.
vớ i dã y nhâ n quả.
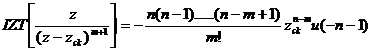 vớ i dã y
vớ i dã y
phả n nhâ n quả.
Ví dụ 1: Cho 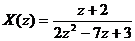
Hã y xá c đ ị nh x(n)
Ví dụ 2: Cho 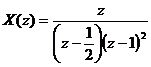
Hã y xá c đ iị nh x(n)
3 Phâ n tí ch hệ thố ng rờ i rạ c trê n miề n z
Chú ng ta đ ã biế t trê n miề n n mộ t HT-TT-BB đ ư ợ c đ ặ c trư ng bở i đ á p ứ ng xung hoặ c phư ơ ng trì nh sai phâ n tuyế n tí nh hệ số hằ ng. Như ng việ c phâ n tí ch hệ thố ng nhiề u khi gặ p phả i sự khó khă n củ a việ c tí nh tí ch chậ p, gả i PT-SP.... Trong phầ n trư ớ c chú ng ta đ ã biể u diễ n tí n hiệ u sang miề n biế n số z, bâ y giờ ta sẽ phâ n tí ch hệ TT-BB trê n miề n z, trư ớ c tiê n ta tì m hiể u khá i niệ m hà m truyề n đ ạ t củ a hệ thố ng.
3. 3 Hà m truyề n đ ạ t củ a hệ thố ng TT-BB
| Miề n n | Miề n z |
y(n) = x(n)*h(n)
= 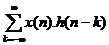 h(n) = IZT[H(z)]
h(n) = IZT[H(z)]
| X(z) = ZT[x(n)], Y(z) = ZT[y(n)]
H(z) = ZT[h(n)]
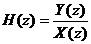
|
Như vậ y hà m truyề n đ ạ t củ a hệ thố ng TT-BB chí nh là biế n đ ổ i z cuả đ á p ứ ng xung củ a nó. Hà m truyề n đ ạ t đ ư ợ c kí hiệ u là H(z) vaà nó cũ ng đ ặ c trư ng hoà n toà n cho hệ thố ng trê n miề n z.
3. 4 Hà m truyề n đ ạ t củ a hệ đ ư ợ c mô tả bở i PT – SP – TT –HSH
Quan hệ giữ a đ ầ u và o và đ ầ u ra củ a mộ t HT – TT – BB đ ư ợ c mô tả bở i PT sau:
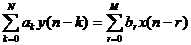 ; lấ y biế n đ ổ i Z 2 vế ta có:
; lấ y biế n đ ổ i Z 2 vế ta có:
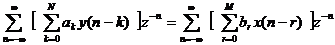
Á p dụ ng tí nh chấ t trễ và tuyế n tí nh ta có:
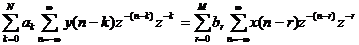
Suy ra: 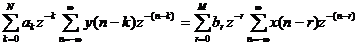
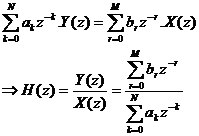
Nế u a0 = 1 thì ta có:
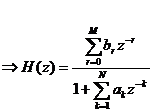
Chú ý: Ta cũ ng có thể biể u diễ n H(z) dư ớ i dạ ng hà m củ a z-1, hoặ c cá c cự c và khô ng củ a nó.
3. 5 Giả i phư ơ ng trì nh sai phâ n TT – HSH sử dụ ng biế n đ ổ i z
Đ ể giả i PT – SP – TT – HSH ta tì m hiể u khá i niệ m biế n đ ổ i z đ ơ n hư ớ ng.
a. Biế n đ ổ i z đ ơ n hư ớ ng
Biế n đ ổ i z đ ơ n hư ớ ng đ ư ợ c đ ị nh nghĩ a như sau:

Cá c tí nh chấ t củ a biế n đ ổ i z đ ơ n hư ớ ng cũ ng giố ng như tí nh chấ t củ a biế n đ ổ i z trừ tí ch chấ t dị ch thờ i gian như sau:
Nế u ZT+ [x(n) ] = X+(z) thì
ZT+ [x(n-k)] = z-k 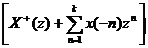 vớ i k > 0
vớ i k > 0
ZT+ [x(n+k)] = zk 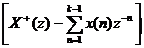 vớ i k < 0
vớ i k < 0
b. Giả i phư ơ ng trì nh sai phâ n:
Ví dụ: Giả i cá c phư ơ ng trì nh sau:
1) y(n) – 3y(n-1) +2y(n-2) = x(n) vớ i x(n) = 3n+2, y(-2) = -4/9, y(-1) =-1/3
2) y(n) = ay(n-1) + x(n) vớ i x(n) = u(n), y(-1) = 1
3. 6 Phâ n tí ch hệ thố ng TT – BB trê n miề n z.
Cá c phầ n tử thự c hiệ n hệ thố ng trê n miề n z cũ ng giố ng như trê n miề n n, chỉ khá c kí hiệ u củ a phầ n tử trễ ta thay D = Z-1
a. Nguyê n tắ c phâ n tí ch hệ thố ng
- Phâ n tí ch hệ tổ ng quá t thà nh cá c hệ nhỏ hơ n ( cá c khố i nhỏ hơ n )
- Tì m mố i quan hệ giữ a cá c khố i nhỏ hơ n nà y.
- Xá c đ ị nh hà m truyề n đ ạ t Hi(z) cua cá c khố i nhỏ.
- Tổ ng hợ p hà m truyề n đ ạ t từ cá ch phâ n tí ch ở trê n.
b. Mộ t số quy tắ c biế n đ ổ i sơ đ ồ khố i
- Hệ gồ m cá c khố i mắ c nố i tiế p
Vẽ hì nh
H(z) = H1(z). H2(z)... Hn(z)
Vậ y hệ gồ m cá c khố i mắ c nố i tiế p sẽ tư ơ ng đ ư ơ ng vớ i hệ thố ng có hà m truyề n đ ạ t là tí ch củ a cá c hà m truyề n đ ạ t thà nh phầ n.
- Hệ gồ m cá c khố i mắ c song song.
Vẽ hì nh
H(z) = H1(z) + H2(z) +... + Hn(z)
Vậ y hệ thố ng gồ m cá c khố i mắ c song song vớ i nhau sẽ tư ơ ng đ ư ơ ng vớ i hệ thố ng có hà m truyề n đ ạ t là tổ ng củ a cá c hà m truyề n đ ạ t thà nh phầ n.
- Hệ có hồ i tiế p
c. Sự ổ n đ ị nh củ a hệ thố ng TT – BB
Đ ố i vớ i mộ t hệ thố ng tuyế n tí nh bấ t biế n, nế u tí n hiệ u ở đ ầ u và o khô ng có như ng ở đ ầ u ra củ a hệ thố ng vẫ n xuấ t hiệ n tí n hiệ u thì hệ thố ng đ ó là hệ thố ng khô ng ổ n đ ị nh.
Trong chư ơ ng trư ớ c chú ng ta đ ã xé t đ ộ ổ n đ ị nh củ a hệ thố ng TT-BB nó đ ư ợ c đ ặ c trư ng bở i cá c tí nh chấ t củ a đ á p ứ ng xung h(n) củ a nó, cụ thể: Mộ t hệ thố ng TT –BB là ổ n đ ị nh nế u đ iề u kiệ n sau đ â y thoả mã n:
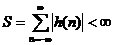
Trong miề n z thì ta có:
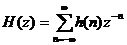 vớ i miề n hộ i tụ củ a nó:
vớ i miề n hộ i tụ củ a nó: 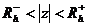
So sá nh vớ i đ iề u kiệ n hộ i tụ trê n miề n n thì ta thấ y đ ể đ iề u kiệ n ổ n đ ị nh trê n miề n n thoả mã n thì H(z) phả i hộ i tụ vớ i 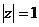 nghĩ a là nó hộ i tụ trê n vò ng trò n đ ơ n vị củ a mặ t phẳ ng z, vì thế miề n hộ i tụ củ a H(z) phả i chứ a vò ng trò n đ ơ n vị.
nghĩ a là nó hộ i tụ trê n vò ng trò n đ ơ n vị củ a mặ t phẳ ng z, vì thế miề n hộ i tụ củ a H(z) phả i chứ a vò ng trò n đ ơ n vị.
Vậ y ta có thể phá t biể u đ iề u kiệ n ổ n đ ị nh củ a mộ t HT – TT –BB trê n miề n z như sau: Mộ t hệ thố ng TT –BB là ổ n đ ị nh khi và chiỉ khi vò ng trò n đ ơ n vị củ a mặ t phẳ ng z nằ m trong miề n hộ i tụ củ a hà m truyề n đ ạ t củ a hệ thố ng.
c2. Sự ổ n đ ị nh củ a hệ thố ng nhâ n quả
Trong thự c tế chú ng ta chỉ gặ p cá c hệ thố ng nhâ n quả ổ n đ ị nh, vì vậ y ta sẽ xé t sự ổ n đ ị nh củ a cá c hệ thố ng nà y.
Do hà m truyề n đ ạ t củ a hệ thố ng nhâ n quả đ ư ợ c viế t như sau:
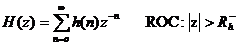 trong đ ó
trong đ ó 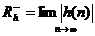 (T/c Cauchy)
(T/c Cauchy)
Từ đ â y ta có mộ t số nhậ n xé t sau:
- Mộ t hệ thố ng là nhâ n quả nế u miề n hộ i tụ củ a hà m truyề n đ ạ t nằ m ngoà i vò ng trò n đ ư ờ ng kí nh R-h
- Đ ố i vớ i HT –TT –BB đ iề u kiệ n nhâ n quả và ổ n đ ị nh là đ ọ c lậ p vớ i nhau. Nghĩ a là hệ thố ng ổ n đ ị nh chư a chắ c đ ã nhâ n quả và ngư ợ c lạ i.
- Trong thự c tế chú ng ta chỉ xé t cá c hệ thố ng thự c hiệ n đ ư ợ c về mặ t vậ t lý đ ó là cá c hệ thố ng ổ n đ ị nh và nhâ n quả.
- Vậ y đ iề u kiệ n đ ể HT –TT –BB nhâ n quả và ổ n đ ị nh là : Miề n hộ i tụ củ a hà m truyề n đ ạ t H(z) củ a nó phả i thoả mã n:
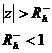
Rõ rà ng miề n hộ i tụ củ a H(z) khô ng chứ a bấ t cứ đ iể m cự c zck nà o do đ ó ta có thể nó i: Mộ t hệ thố ng TT –BB nhâ n quả và ổ n đ ị nh khi và chỉ khi tấ t cả cá c đ iể m cự c củ a hà m truyề n đ ạ t nằ m trong vò ng trò n đ ơ n vị.
Ví dụ 1:
HT – TT – BB đ ư ợ c cho như sau:
y(n) = a. y(n-1) + x(n)
- Tì m H(z), h(n)
- Xé t sự ổ n đ ị nh củ a hệ nhâ n quả
Giả i:
- Lấ y biế n đ ổ i z 2 vế củ a pt ta có:
Y(z) = a. z-1Y(z) + X(z)
Suy ra 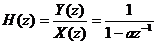
H(z) có 1 đ iể m cự c là zc =a
Nế u H(z) là hà m truyề n đ ạ t củ a hệ nhâ n quả thì ta có ROC: 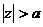 thì ta có:
thì ta có:
h(n) = IZT[H(z)] = anu(n)
Nế u H(z) là hà m truyề n đ ạ t củ a hệ phả n nhâ n quả thì ta có ROC: 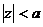 thì ta có:
thì ta có:
h(n) = IZT[H(z)] = -anu(-n-1)
- Sự ổ n đ ị nh củ a hệ nhâ n quả: Theo đ iề u kiệ n củ a hệ nhâ n quả ổ n đ ị nh thì ta phá i có a< 1 thì hệ nhâ n quả trê n sẽ ổ n đ ị nh
Ví dụ 2:
Xé t sự ổ n đ ị nh củ a HT nhâ n quả có hà m truyề n đ ạ t sau:
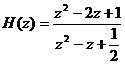
Tì m cá c zck, hệ có zc1=1/2 + j1/2, zc1=1/2- j1/2
Đ â y là 2 đ iể m cự c nằ m trong vò ng trò n đ ơ n vị vậ y HT nhâ n quả đ ã cho là ổ n đ ị nh.
c3. Tiê u chuẩ n July (Giá o trì nh )
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|