
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№37. Критерий согласия . Пример.
Постановка задачи.
Имеется некоторая случайная величина 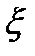 , распределённая по закону
, распределённая по закону 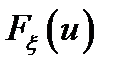 . Формулируется утверждение
. Формулируется утверждение 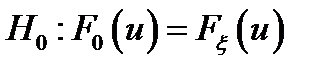 (1), где
(1), где 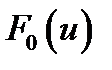 – предполагаемая функция распределения. (1) – основная гипотеза (утверждение о том, что
– предполагаемая функция распределения. (1) – основная гипотеза (утверждение о том, что 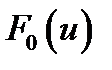 имеет конкретный вид). Ей противопоставляется гипотеза
имеет конкретный вид). Ей противопоставляется гипотеза 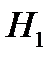 (она содержит все распределения, которые могут быть, но не соответствуют основной гипотезе) – альтернативная гипотеза (
(она содержит все распределения, которые могут быть, но не соответствуют основной гипотезе) – альтернативная гипотеза ( 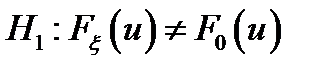 ).
).
Критерий согласия 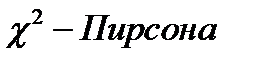 .
.
Чтобы использовать данный критерий, необходимо составить группированную выборку:
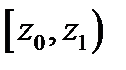
| 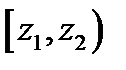
| 
| 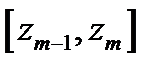
|
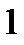
| 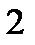
| 
| 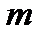
|
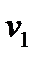
| 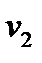
| 
| 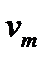
|
Составляется статистика 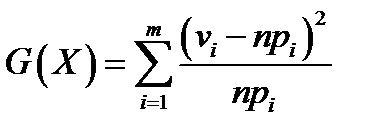 – статистика Пирсона (
– статистика Пирсона ( 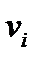 – практическое значение выборки,
– практическое значение выборки, 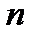 – объём выборки,
– объём выборки, 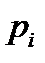 – вероятность попадания в
– вероятность попадания в 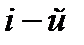 интервал, исходя из предположения закона распределения).
интервал, исходя из предположения закона распределения).
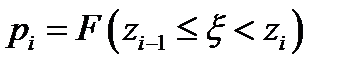
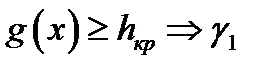 (отвергнуть основную гипотезу и принять альтернативу),
(отвергнуть основную гипотезу и принять альтернативу), 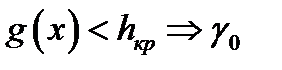 (принять основную гипотезу). Здесь
(принять основную гипотезу). Здесь 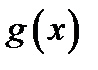 – значение статистики,
– значение статистики, 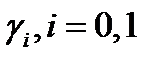 – выводы,
– выводы, 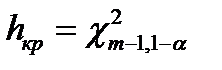 – квантиль распределения
– квантиль распределения 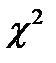 с
с 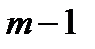 степенями свободы порядка
степенями свободы порядка 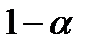 , где
, где 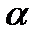 – уровень значимости критерия (вероятность отвергнуть гипотезу
– уровень значимости критерия (вероятность отвергнуть гипотезу 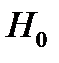 , если она на самом деле верна).
, если она на самом деле верна).
Пример: Произведено 4040 подбрасываний монеты. Герб выпал 2048 раз. Справедлива ли при 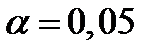 гипотеза о том, что монета симметрична?
гипотеза о том, что монета симметрична?
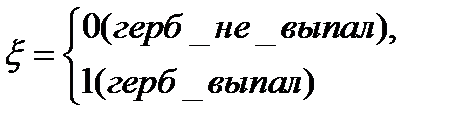 ;
; 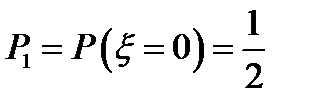 ;
; 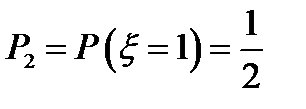 ;
; 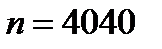 ;
; 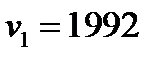 ;
; 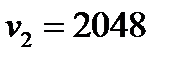
Подставляем значения: 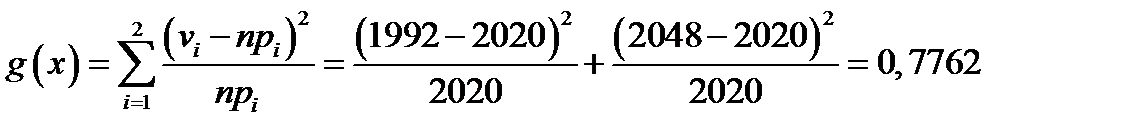 .
.
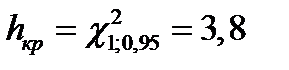 (из таблицы),
(из таблицы), 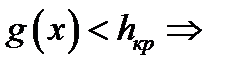 необходимо принять основную гипотезу (монета симметрична).
необходимо принять основную гипотезу (монета симметрична).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|