24. Распределения , Стьюдента (Госсета), Фишера. Их характеристики и свойства.

24. Распределения, Стьюдента (Госсета), Фишера. Их характеристики и свойства.

Распределение .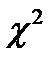

Рассмотрим гамма распределение (описывает времена безотказной работы различных технических устройств) с плотностью 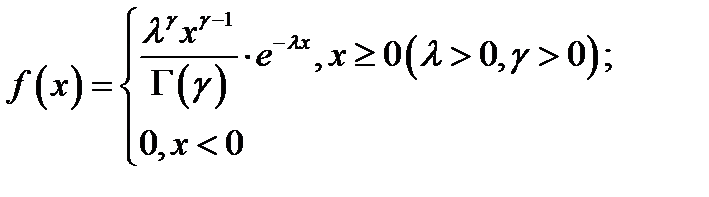, где 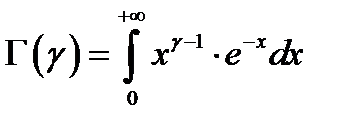– гамма-функция Эйлера.

Если , где 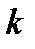– нечётное число, а 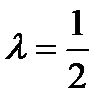, то гамма-распределение превращается в распределение 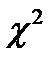(хи-квадрат). Параметр 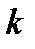называют в этом случае числом степеней свободы распределения .

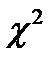Распределение Стьюдента (Госсета).

Распределением Стьюдента ( 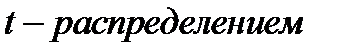) называют распределение с плотностью .

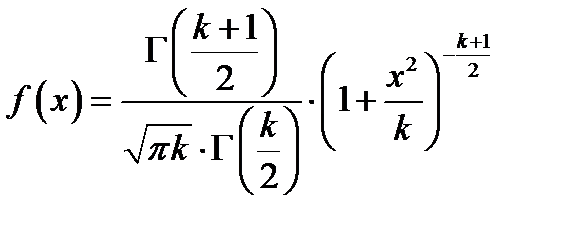Распределение Фишера (Снедекора).

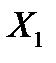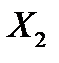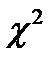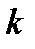Пусть независимые случайные величины и имеют распределение с и 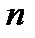степенями свободы соответственно. Распределением Фишера ( ) называется распределение случайной величины 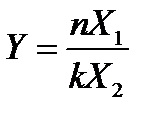, плотность которого выражается следующей формулой: .

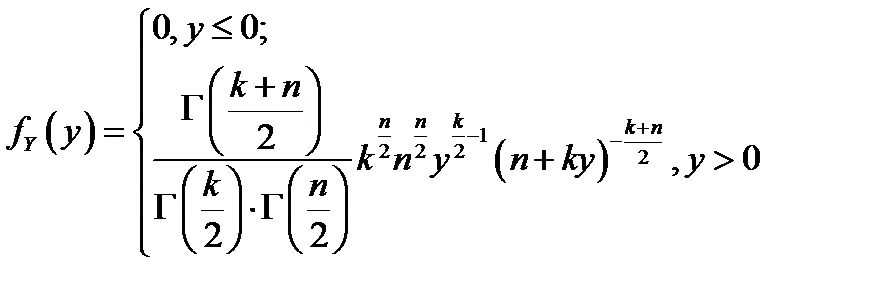№27. Случайная выборка и генеральная совокупность. Закон распределения выборки.

Математическая статистика – раздел прикладной математики, посвящённый методам систематизации и анализа статистических данных с целью построения вероятностной модели случайных явлений, а также уточнения их параметров.

Сопоставляя задачи теории вероятностей и математической статистики, можно говорить о том, что задачи математической статистики являются теоретически обработанными выводами теории вероятностей. В задачах теории вероятностей, как правило, вероятностная модель дана, и необходимо по одним её параметрам получить другие. В задачах математической статистики неизвестна либо вся вероятностная модель, либо её параметры, и необходимо, основываясь на статистических данных, получить неизвестные части вероятностной модели или вынести определённые суждения о них.

Таким образом исходными для задач математической статистики являются статистические данные, которые как правило имеют численную природу. Статистические данные получаются в результате статистического эксперимента, заключающегося в измерении значения некоторой случайной величины. Результаты измерений записываются последовательно.

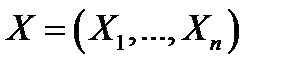– выборка объёма 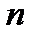, 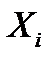– элементы выборки. 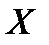– многомерная случайная величина, т. к. результат 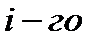измерения заранее предсказать нельзя. В результате конкретного измерения получается реализация выборки 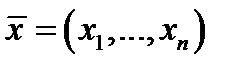, где 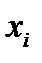– выборочные значения.

Необходимым условием решения задач математической статистики является условие репрезентативности, т. е. выборка должна отражать закон распределения случайной величины.

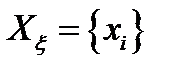– генеральная совокупность (множество всех возможных выборочных значений). Выборка взята из генеральной совокупности 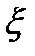, если она получена из измерения случайной величины .

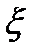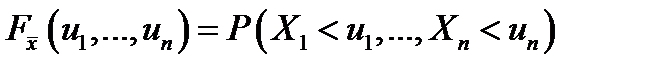– закон распределения выборки. В случае независимости измерений .

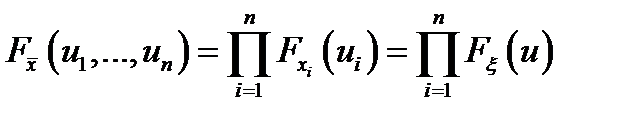Если выборка репрезентативна, то каждый её элемент имеет то же распределение, что и наблюдаемая случайная величина: .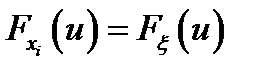

По умолчанию считаем измерения независимыми.

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒