№33. Метод моментов для точечных оценок. Пример.

Метод моментов был предложен английским статистиком К. Пирсоном и является одним из первых общих методов оценивания. Он состоит в следующем.

Пусть имеется случайная выборка 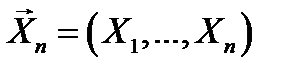из генеральной совокупности 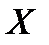, распределение которой 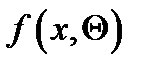известно с точностью до вектора параметров 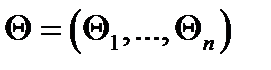. Требуется найти оценку параметра по случайной выборке .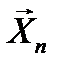

Будем предполагать, что у случайной величины 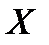существуют первые 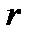моментов: 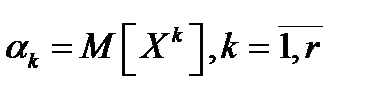. Ясно, что величины 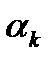являются функциями неизвестного вектора параметров , т. е. .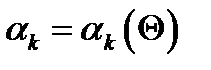

Рассмотрим выборочные моменты 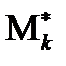(или же ).

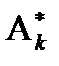Выборочные моменты являются состоятельными оценками соответствующих моментов генеральной совокупности 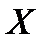, поэтому при большом объёме выборк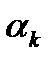и и 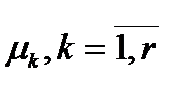, можно заменить соответственно моментам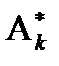и и 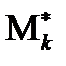выборки .

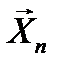В методе моментов в качестве точечной оценки 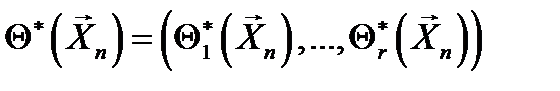вектора параметров берут статистику, значение которой для любой реализации 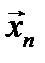случайной выборки 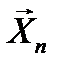получают как решение системы уравнений .

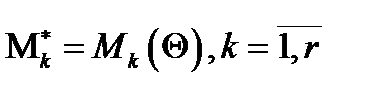Пример: Методом моментов найдём оценку параметра 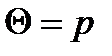в биномиальной модели, где 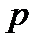есть вероятность «успеха» в любом из 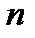независимых повторных наблюдений, а случайная величина 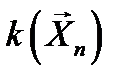– число «успехов». Случайной выборкой 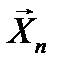в данном случае является 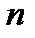дискретных случайных величин 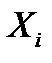, каждая из которых принимает значение 1 с вероятностью 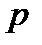и 0 – с вероятностью . При этом 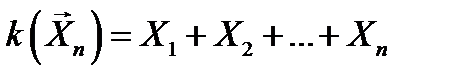, а математическое ожидание 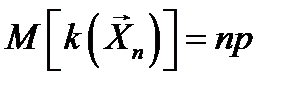. Если в результате 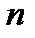независимых наблюдений мы получили выборочное значение 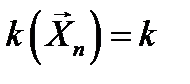, то уравнение, которое нужно составить согласно методу моментов, имеет вид 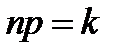. Получаем 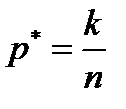. Следовательно, точечной оценкой параметра 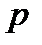является относительная частота.

⇐ Предыдущая 11 12 13 14 15 16 17 181920 Следующая ⇒