Хелпикс

Главная

Контакты

Случайная статья



№30. Точечные оценки и их свойства.

⇐ ПредыдущаяСтр 17 из 20Следующая ⇒


    Постановка задачи точечного оценивания.

    Пусть 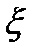 – случайная величина, 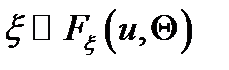, т. е. закон распределения  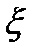зависит от , в общем случае векторного: 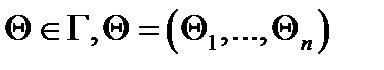,  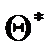– точечная оценка параметра ,  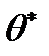– её значение.

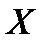     – выборка объёма  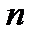из генеральной совокупности 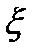. Требуется, используя информацию, содержащуюся в выборке, указать в параметрическом множестве 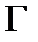значение параметра .

    Метод решения задачи.

    Строится функция выборки 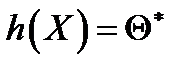, значение которой при конкретной реализации выборки принимают а истинное значение параметра , .

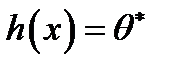    Замечание: оцениваться может не сам параметр , а некоторая параметрическая функция 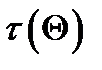.  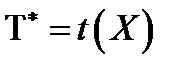– сама оценка (функция),  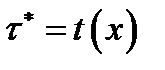– её значение. .

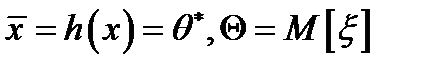    Функций выборки в качестве оценок можно предложить множество. Чтобы выбрать подходящую, существуют определённые характеристики (свойства точечных оценок).

    Статистику 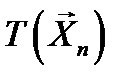 называют достаточной для параметра , если условная функция распределения 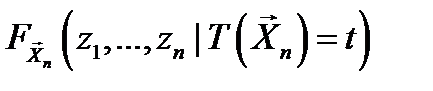 случайной выборки  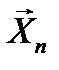при условии  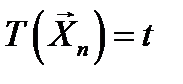не зависит от параметра  при любом возможном значении .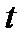

    Свойства точечных оценок:

1. Несмещённость. 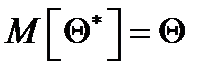, для параметрической функции .

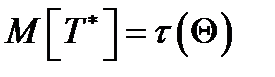2. Эффективность. Эффективной называется несмещённая оценка с минимальной дисперсией. 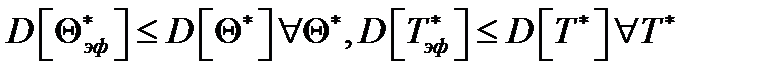. Относительная эффективность: 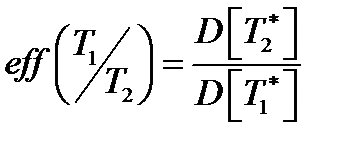,  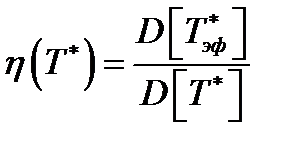– коэффициент эффективности.

3. Состоятельность. Состоятельной является оценка, которая сходится по вероятности к тому, что она оценивает: . ( ).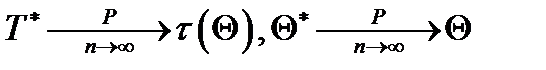


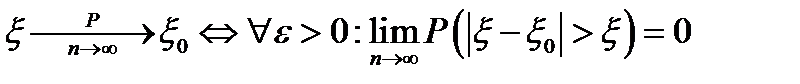⇐ Предыдущая11121314151617181920Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.