
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№18. Числовые характеристики случайного вектора.
№18. Числовые характеристики случайного вектора.
Пусть 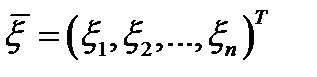 – случайный вектор, тогда
– случайный вектор, тогда 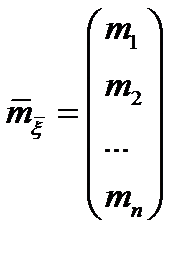 – математическое ожидание случайного вектора
– математическое ожидание случайного вектора 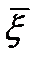 ,
, 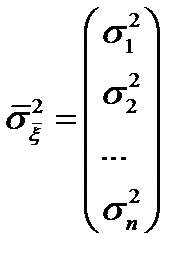 – его дисперсия.
– его дисперсия.
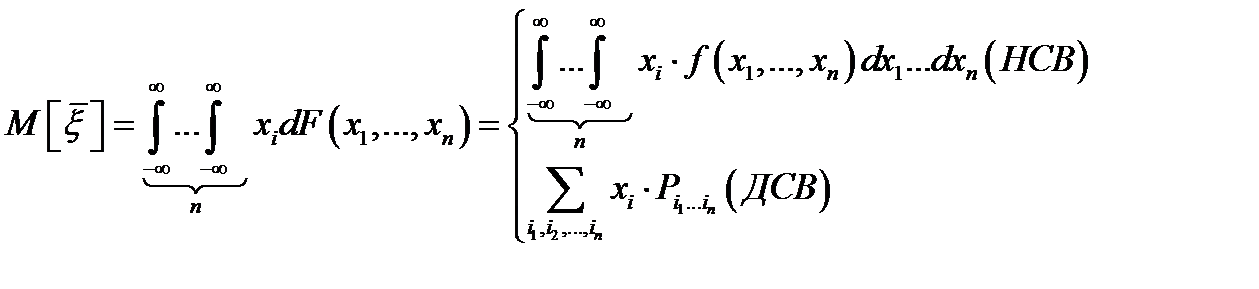
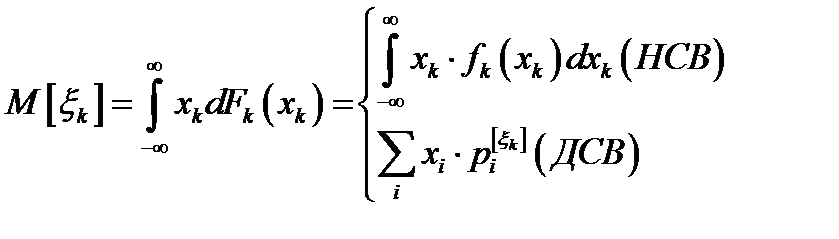
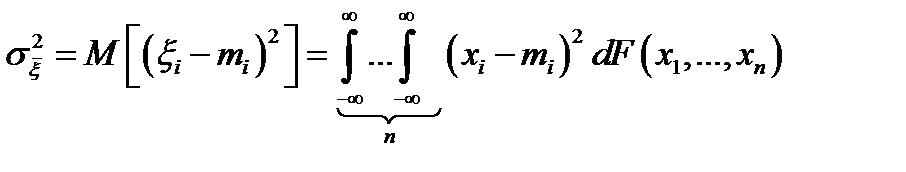
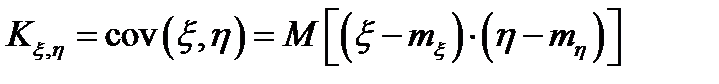 – ковариация (корреляционный момент)
– ковариация (корреляционный момент)
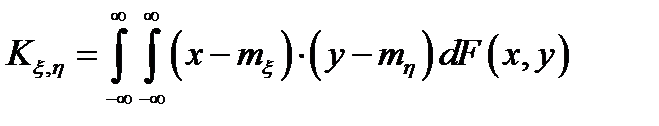
Свойства ковариации:
1. 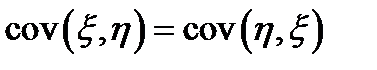 ;
;
2. 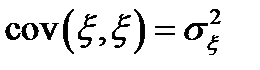 ;
;
3. 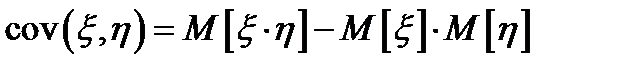
Доказательство: 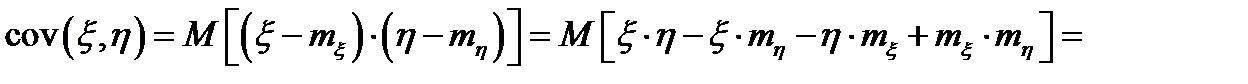
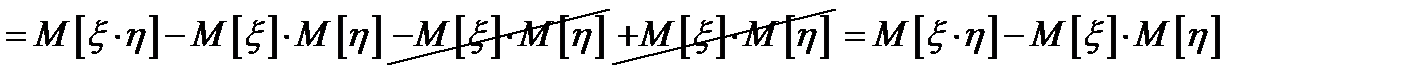 , ч. т. д
, ч. т. д
4. Если 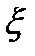 и
и 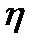 независимы, то
независимы, то 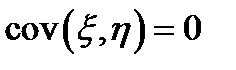 .
.
№19. Коэффициент корреляции и его свойства. Корреляционная матрица.
Коэффициентом корреляции 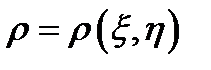 двух случайных величин
двух случайных величин 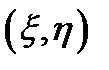 называется безразмерная величина
называется безразмерная величина 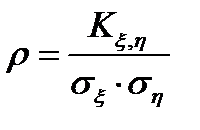 , где
, где 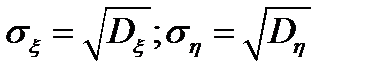 . Коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами. Независимые случайные величины являются некоррелированными (для них
. Коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами. Независимые случайные величины являются некоррелированными (для них 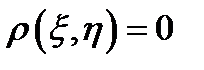 ).
).
Свойства:
1. 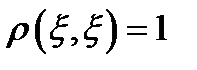 ;
;
2. Если 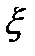 и
и 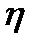 независимы, то
независимы, то 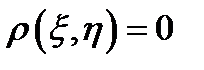 ;
;
3. 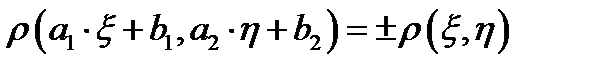 , при этом знак «плюс» нужно брать в том случае, когда
, при этом знак «плюс» нужно брать в том случае, когда 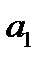 и
и 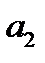 имеют одинаковые знаки, и минус – в противном случае;
имеют одинаковые знаки, и минус – в противном случае;
4. 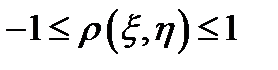 ;
;
5. 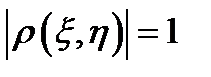 тогда и только тогда, когда случайные величины
тогда и только тогда, когда случайные величины 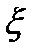 и
и 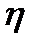 связаны линейной зависимостью (т. е.
связаны линейной зависимостью (т. е. 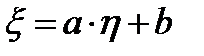 ).
).
Корреляционной матрицей системы 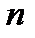 случайных величин
случайных величин 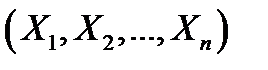 называется таблица, составленная из корреляционных моментов всех этих величин, взятых попарно
называется таблица, составленная из корреляционных моментов всех этих величин, взятых попарно 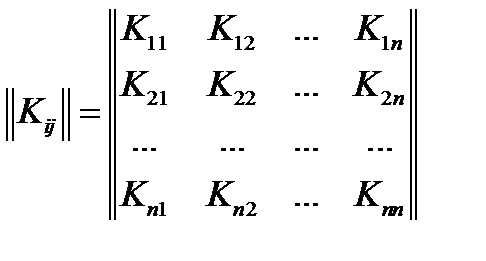 , где
, где 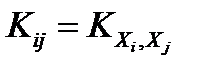 – корреляционный момент случайных величин
– корреляционный момент случайных величин 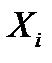 и
и 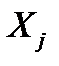 .
.
Корреляционная матрица симметрична, поэтому обычно заполняется лишь половина таблицы, 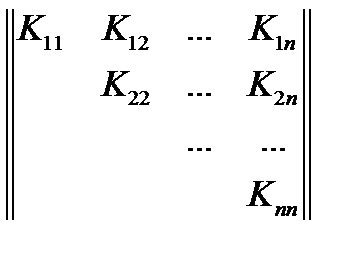 .
.
По главной диагонали корреляционной матрицы стоят дисперсии случайных величин 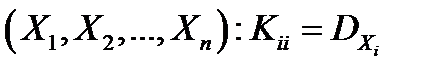 .
.
Нормированной корреляционной матрицей системы 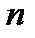 случайных величин называется таблица, составленная из коэффициентов корреляции всех этих величин, взятых попарно,
случайных величин называется таблица, составленная из коэффициентов корреляции всех этих величин, взятых попарно, 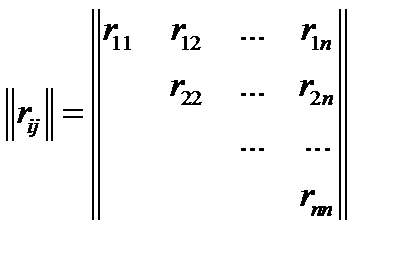 , где
, где 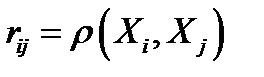 – коэффициент корреляции величин
– коэффициент корреляции величин 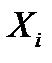 и
и 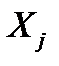 . По главной диагонали нормированной корреляционной матрицы стоят единицы.
. По главной диагонали нормированной корреляционной матрицы стоят единицы.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|