Хелпикс

Главная

Контакты

Случайная статья



№28. Оценка вероятности события. Оценка функции распределения. Оценка плотности вероятностей.

⇐ ПредыдущаяСтр 16 из 20Следующая ⇒


№28. Оценка вероятности события. Оценка функции распределения. Оценка плотности вероятностей.

    Оценка вероятности события.

    Пусть 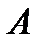– случайное событие. Необходимо построить оценку вероятности .

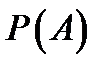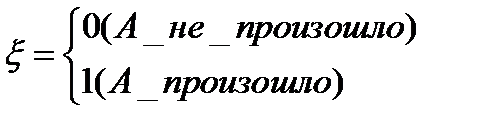    , тогда .

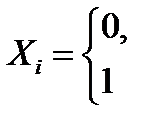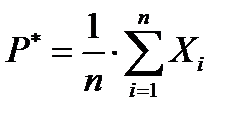     – оценка,  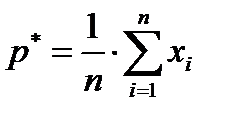– значение оценки.

    Оценка функции распределения.

    Дана выборка 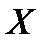из 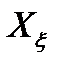. Необходимо оценить .

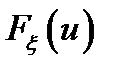    Сначала функция распределения представляется в виде 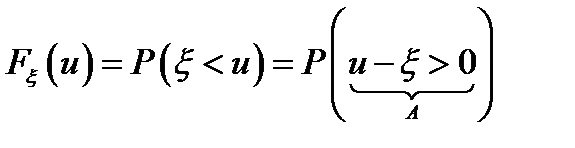. Т. о. задачу можно свести к оценке вероятности события:

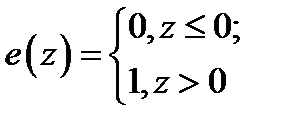    , тогда  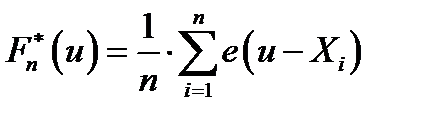– оценка функции распределения,  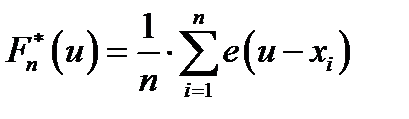– эмпирическая функция распределения.

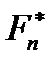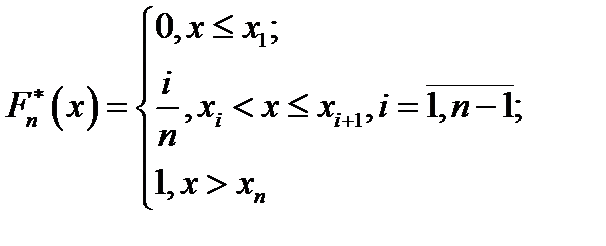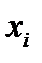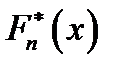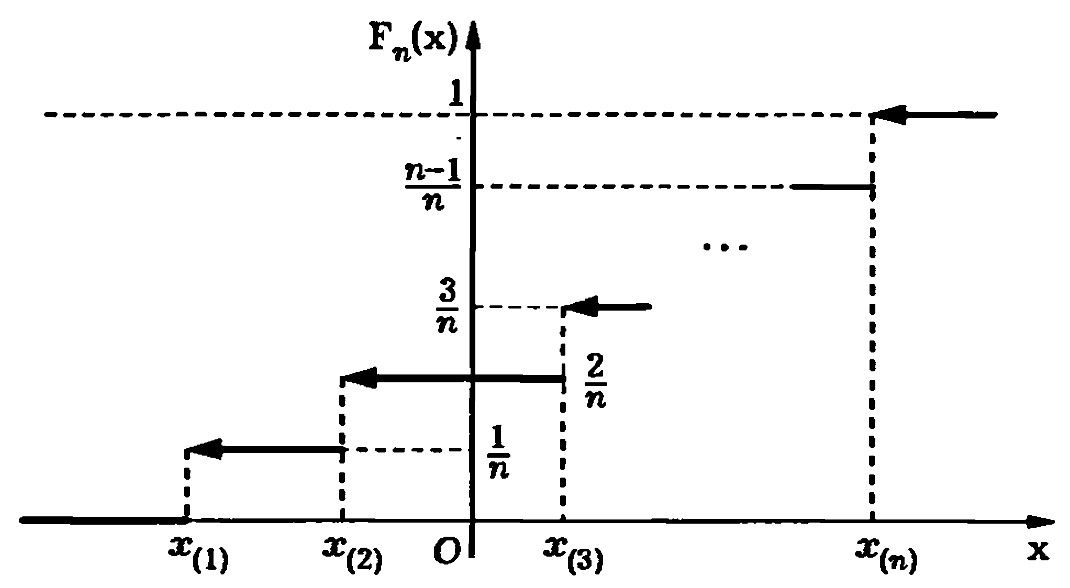
    1. Если все выборочные значения  различны, то функцию  можно записать в следующем виде: , т. е. в каждой точке  функция  имеет скачок величиной 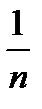. На рисунке изображён график функции :

 

        

 

 

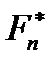2. Группированная выборка. 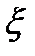 – непрерывная случайная величина,  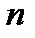– достаточно большое число. Разобьём множество значений  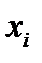на интервалы 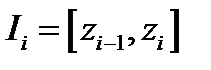, получим группированную выборку:

Номер интервала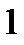
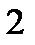
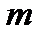
Сам интервал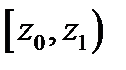
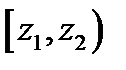
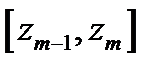
Количество знач.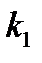

        

; .

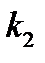
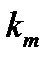
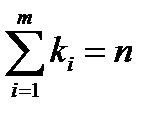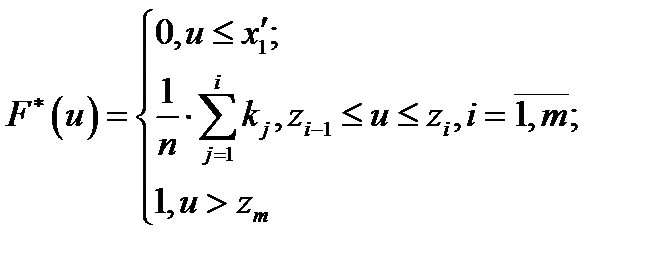Оценка плотности вероятностей.

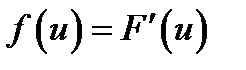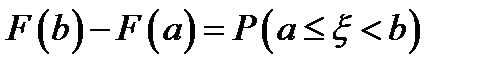    , , а с другой стороны  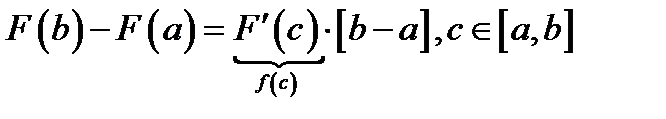– формула конечных приращений Лагранжа.

    , .

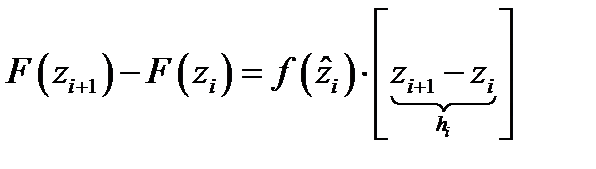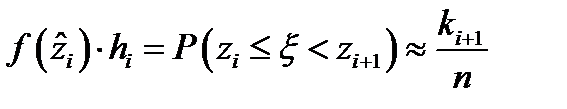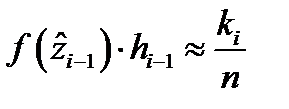    , где 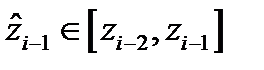,  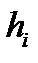– длина  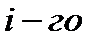отрезка.

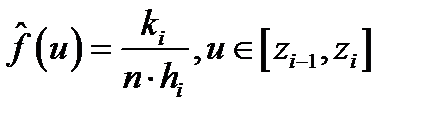     – оценка плотности распределения.

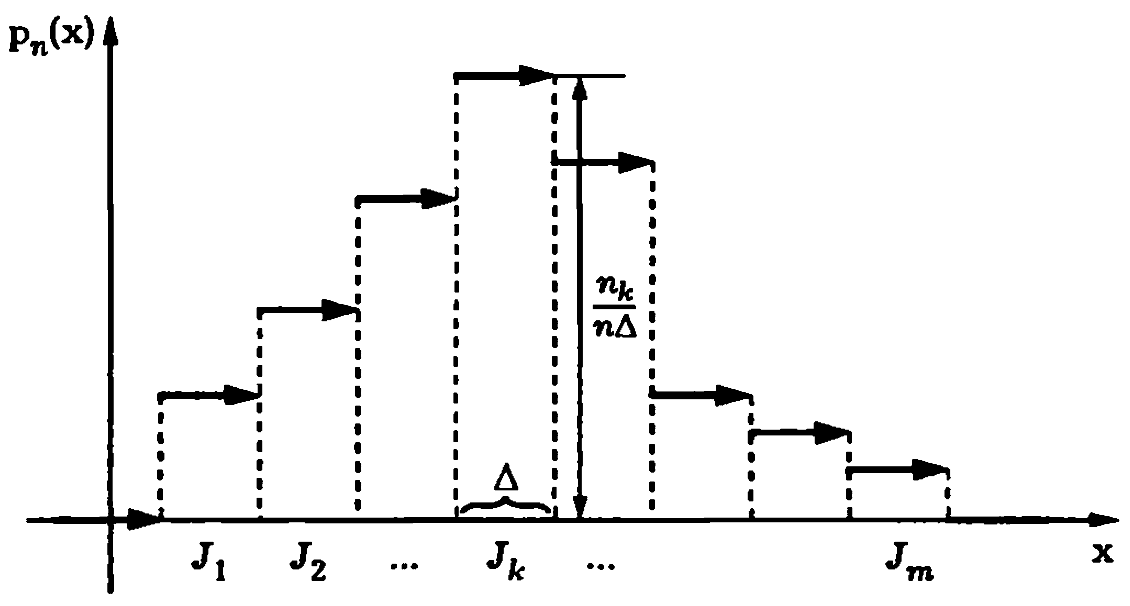    График плотности распределения (гистограмма) изображён на рисунке:

 

№29. Выборочные моменты. Несмещённость выборочного среднего как оценки математического ожидания. Смещённость выборочной дисперсии как оценки теоретической дисперсии.

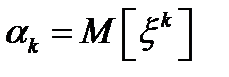     – начальный момент  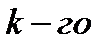порядка.

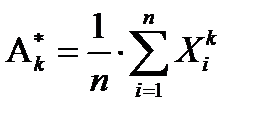     – выборочный начальный момент  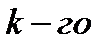порядка,  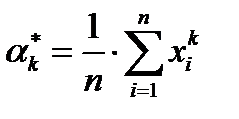– его значение.

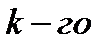     – центральный момент  порядка.

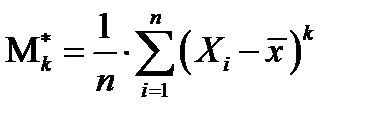     – выборочный центральный момент  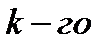порядка,  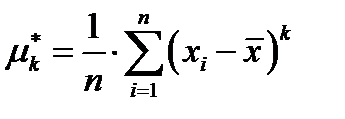– его значение.

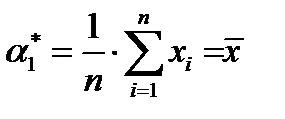     – выборочное среднее (математическое ожидание).

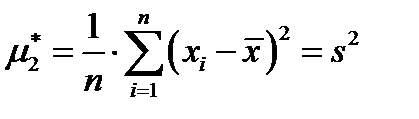     – выборочная дисперсия.

    Для группированной выборки: .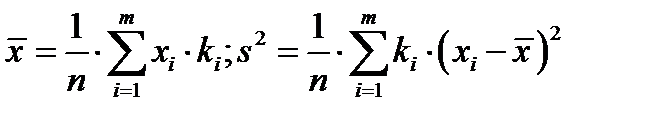

    Пусть 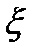 – случайная величина, 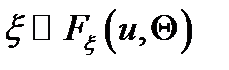, т. е. закон распределения  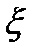зависит от ,  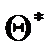– точечная оценка параметра ,  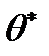– её значение.

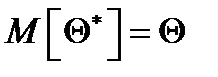     – свойство несмещённости.

    Найдём 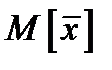 ( 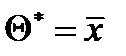– выборочное среднее, ).

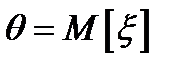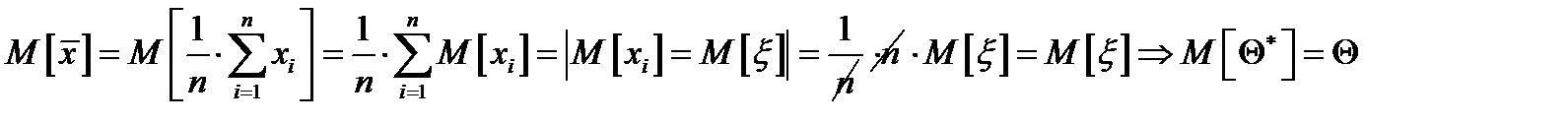    . Т. о. выборочное среднее является несмещённой оценкой математического ожидания.

    Пусть теперь 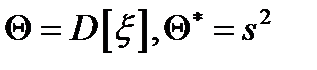. Проверим данную оценку на несмещённость.

   

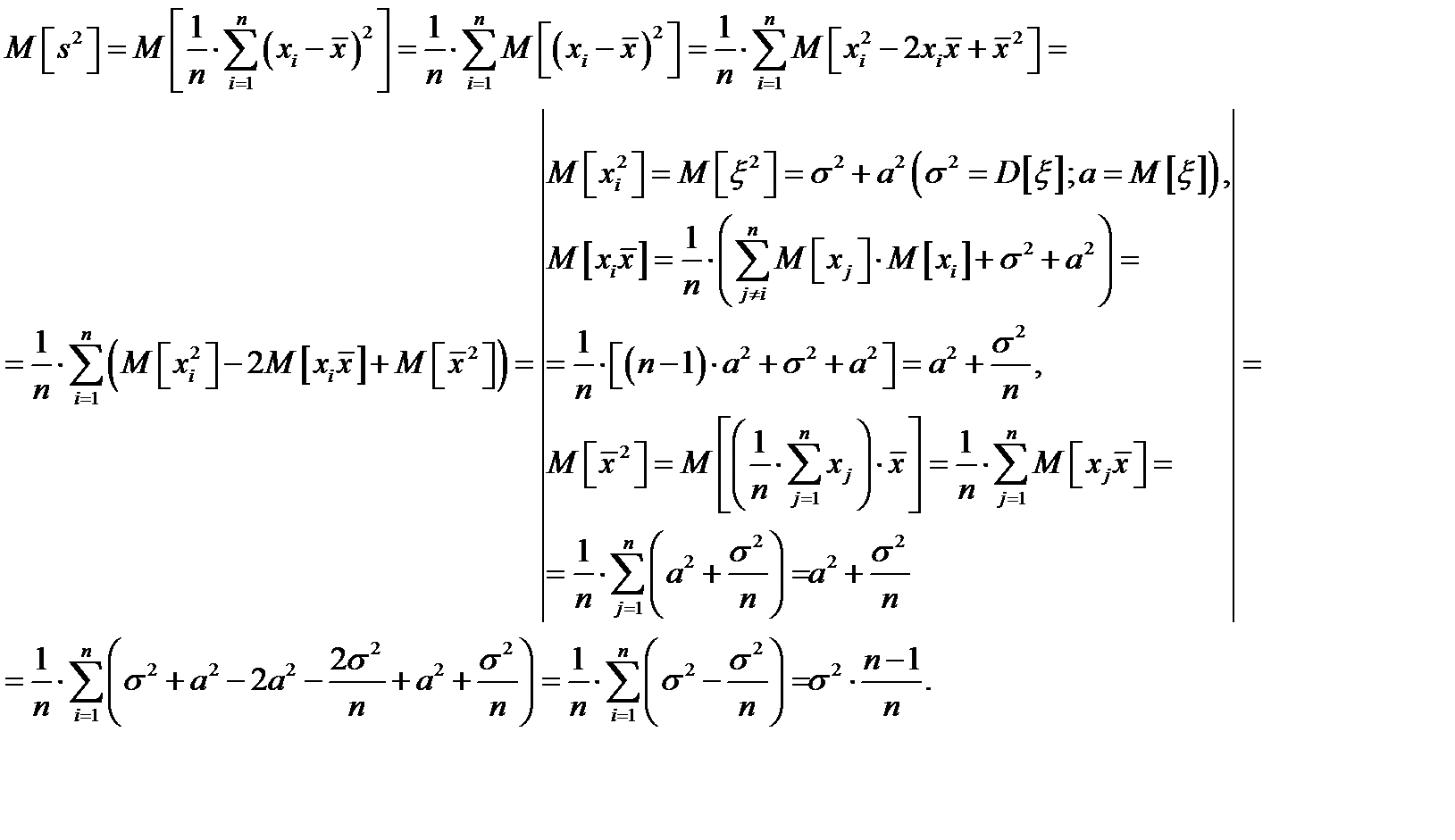
    Т. о. выборочная дисперсия является смещённой оценкой теоретической дисперсии ( 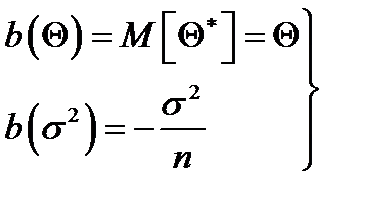– смещение).


⇐ Предыдущая11121314151617181920Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.