№21. Плотность вероятности функции случайной величины при заданной плотности вероятности аргумента. Закон распределения суммы случайных величин. Пример.

Пусть 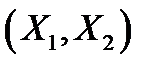– двумерная непрерывная случайная величина с плотностью распределения 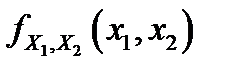. Функцию распределения случайной величины 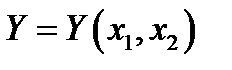можно найти по формуле: 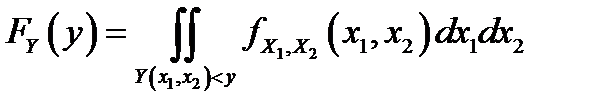(1), где область интегрирования состоит из всех значени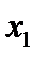й и 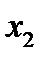, для которых .

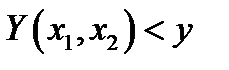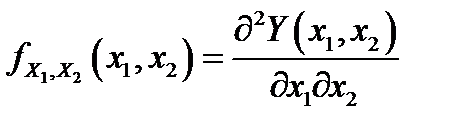– плотность распределения функции .

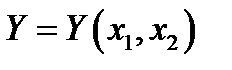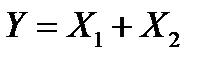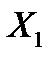Пусть , где и 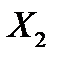– независимые случайные величины, тогда по формуле (1) находим: .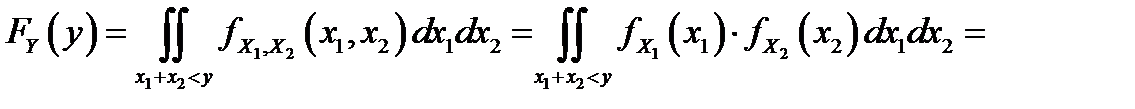

Дифференцируя последнюю формулу по 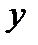под знаком интеграла, получаем (с учётом переобозначения ) выражение для плотности 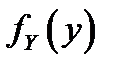распределения суммы 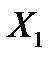и 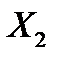: 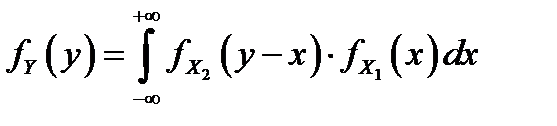(2). В этом случае говорят, что плотность распределения 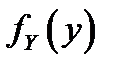случайной величины 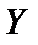является свёрткой (композицией) плотностей распределения 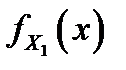и 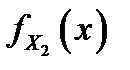слагаемых 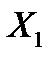и 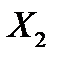или что закон распределения суммы двух независимых случайных величин является свёрткой (композицией) законов распределения слагаемых. Соотношение (2) условно записывают в виде .

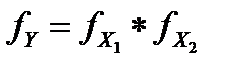Формулу (2) называют формулой свёртки для плотностей распределения случайных величин 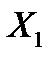и .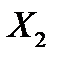

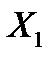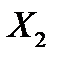Пример: Пусть и – независимые случайные величины, распределённые по нормальному закону со средними значениям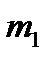и и 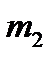и средними квадратичными отклонениям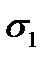и и 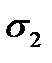. Найдём плотность распределения суммы .

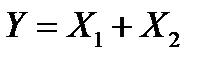Воспользовавшись формулой свёртки, имеем: .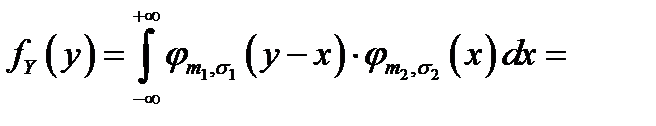

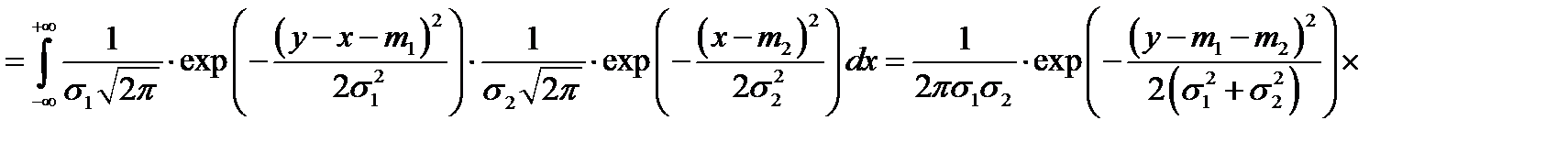
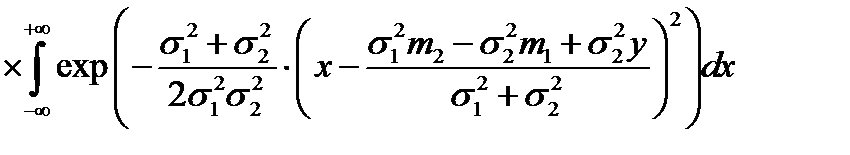Делая теперь замену , получаем: .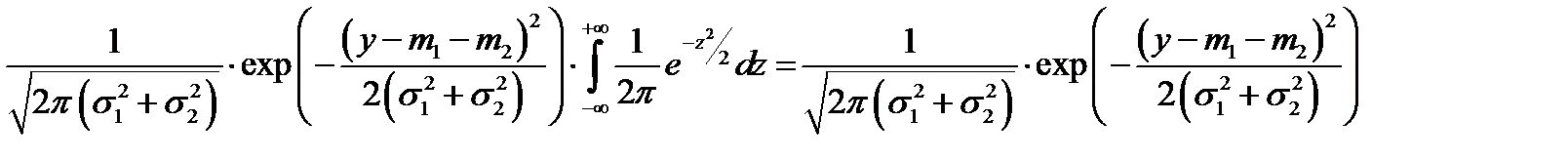

Таким образом, случайная величина 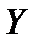также распределена по нормальному закону с параметрами и 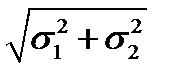, т. е. композиция плотностей нормальных законов распределения является плотностью нормального закона распределения.

⇐ Предыдущая 8 9 10 11 121314 15 16 17 Следующая ⇒