Хелпикс

Главная

Контакты

Случайная статья



№22. Характеристическая функция и её свойства.

⇐ ПредыдущаяСтр 14 из 20Следующая ⇒


№22. Характеристическая функция и её свойства.

    Характеристической функцией случайной величины 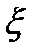 называется математическое ожидание случайной величины 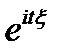: 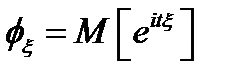. Если  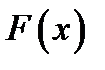есть функция распределения величины 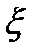, то характеристическая функция равна: .

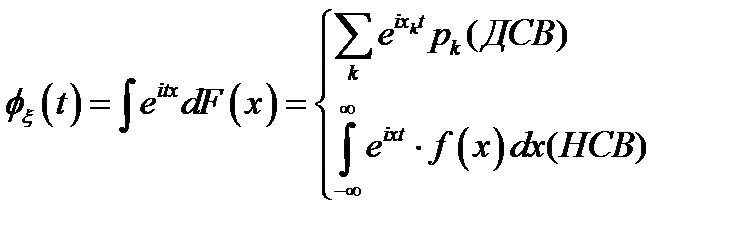    Свойства:

1. Характеристическая функция равномерно непрерывна на всей прямой и удовлетворяет следующим соотношениям: ;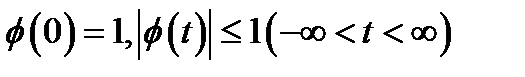

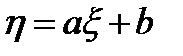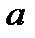2. Если , где  и 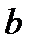 – постоянные, то .

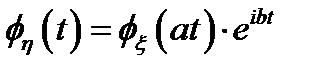3. Характеристическая функция суммы двух независимых случайных величин равна произведению их характеристических функций.

№23. Характеристическая функция и моменты случайной величины.

    Характеристическая функция.

    Характеристической функцией случайной величины 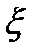 называется математическое ожидание случайной величины 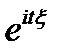: 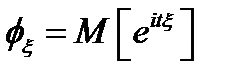. Если  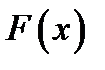есть функция распределения величины 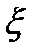, то характеристическая функция равна: .

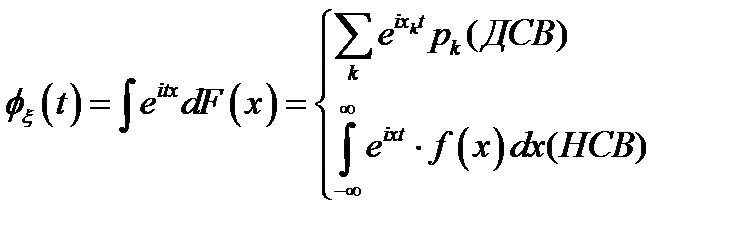    Моменты случайной величины.

    Начальным моментом порядка 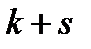 системы  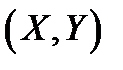называется величина .

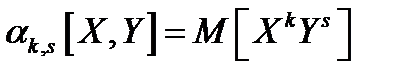    Центральным моментом порядка 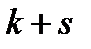 системы  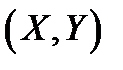называется величина 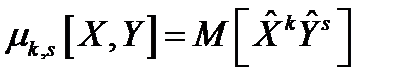, где .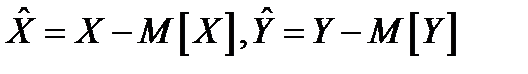

    Расчётные формулы для определения моментов:

    а) Для дискретных случайных величин.

   

   

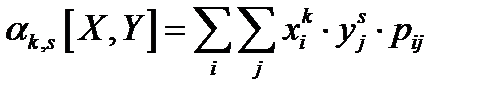
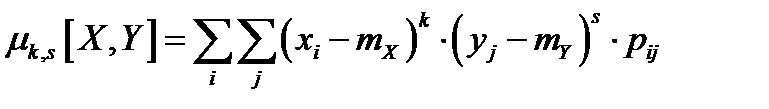
    б) Для непрерывных случайных величин.

    ,

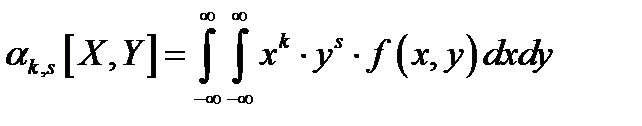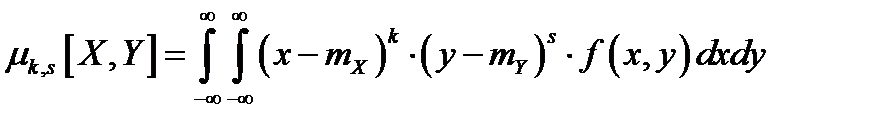    , где 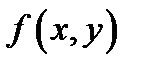– плотность распределения системы.

    Корреляционным моментом 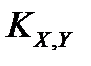 двух случайных величин  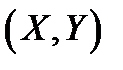называется центральный момент порядка 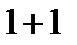, т. е.  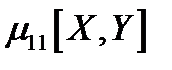(второй смешанный центральный момент): .


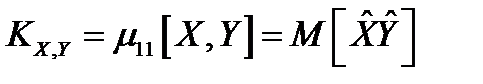⇐ Предыдущая9101112131415161718Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.