
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№20. Ряд распределения функции дискретной случайной величины.
Рассмотрим на вероятностном пространстве 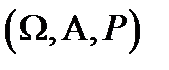 двумерный случайный вектор
двумерный случайный вектор 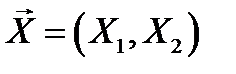 и числовую функцию
и числовую функцию 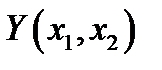 числовых аргументов
числовых аргументов 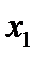 и
и 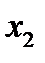 .
.
Случайную величину  называют функцией (скалярной) от двумерной случайной величины (двумерного случайного вектора)
называют функцией (скалярной) от двумерной случайной величины (двумерного случайного вектора) 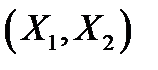 . Функция
. Функция 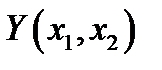 от двумерной дискретной случайной величины является дискретной случайной величиной, принимающей значения
от двумерной дискретной случайной величины является дискретной случайной величиной, принимающей значения 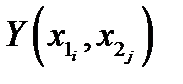 с вероятностью
с вероятностью 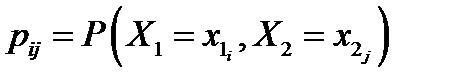 , где
, где 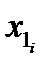 и
и 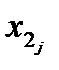 – значения случайных величин
– значения случайных величин 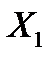 и
и 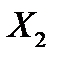 соответственно.
соответственно.
Чтобы построить ряд распределения дискретной случайной величины 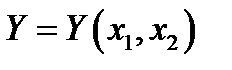 , необходимо, во-первых, не учитывать все те значения
, необходимо, во-первых, не учитывать все те значения 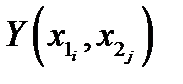 , вероятность принять которые случайной величине
, вероятность принять которые случайной величине 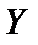 равна нулю, а во-вторых, объединить в один столбец все одинаковые значения
равна нулю, а во-вторых, объединить в один столбец все одинаковые значения 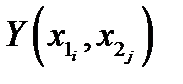 случайной величины
случайной величины 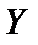 , приписав этому столбцу суммарную вероятность.
, приписав этому столбцу суммарную вероятность.
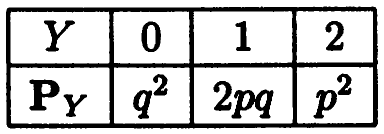
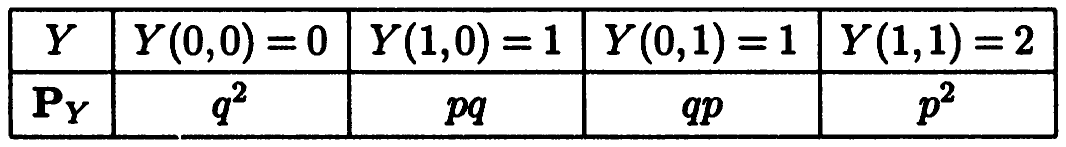 Пример: Пусть
Пример: Пусть 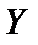 – случайная величина, равная суммарному числу успехов в двух испытаниях по схеме Бернулли, а
– случайная величина, равная суммарному числу успехов в двух испытаниях по схеме Бернулли, а 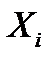 – число успехов в
– число успехов в 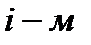 испытании,
испытании, 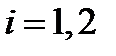 . Тогда
. Тогда 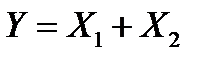 и
и 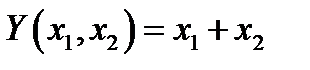 . Заметим, что двум средним столбцам соответствует одно и то же значение 1 случайной величины
. Заметим, что двум средним столбцам соответствует одно и то же значение 1 случайной величины 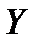 , и их следует объединить. Окончательно получаем ряд распределения случайной величины
, и их следует объединить. Окончательно получаем ряд распределения случайной величины 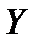 , представленный в следующей таблице:
, представленный в следующей таблице:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|