
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№16. Нормальный случайный вектор.
№16. Нормальный случайный вектор.
Введём двумерное нормальное распределение случайного вектора  .
.
Пусть координаты 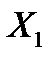 и
и 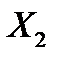 случайного вектора
случайного вектора  являются случайными величинами, распределёнными по нормальному закону, т. е. имеют плотности распределения
являются случайными величинами, распределёнными по нормальному закону, т. е. имеют плотности распределения 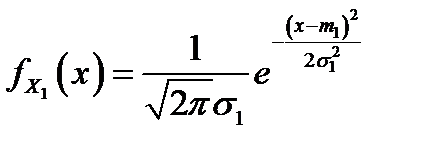 и
и 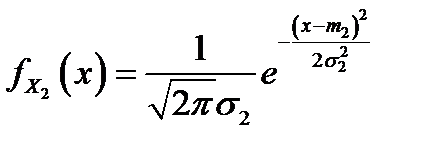 . Если
. Если 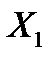 и
и 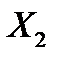 являются независимыми случайными величинами, то
являются независимыми случайными величинами, то 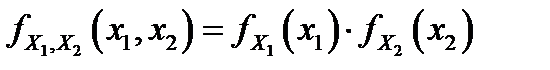 , и в этом случае плотность распределения двумерного нормального распределения имеет вид
, и в этом случае плотность распределения двумерного нормального распределения имеет вид 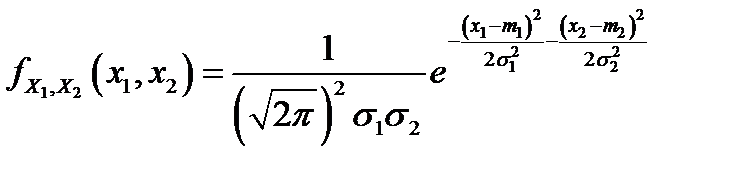 . В общем случае вектор
. В общем случае вектор  имеет (невырожденное) двумерное нормальное распределение, если его плотность распределения определяется формулой
имеет (невырожденное) двумерное нормальное распределение, если его плотность распределения определяется формулой 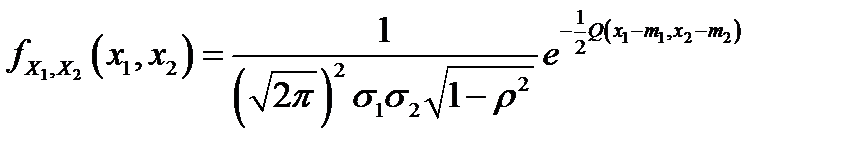 , где функция двух переменных
, где функция двух переменных 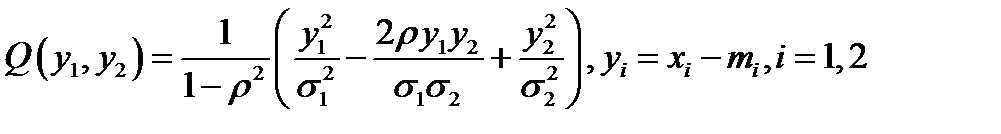 есть положительно определённая квадратичная форма (т. е.
есть положительно определённая квадратичная форма (т. е. 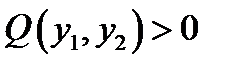 для любых
для любых 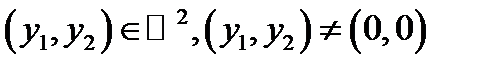 ).
).
Двумерное нормальное распределение зависит от пяти параметров:
– координат 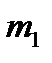 и
и 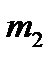 вектора
вектора 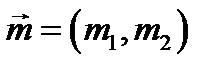 , называемого вектором математических ожиданий вектора
, называемого вектором математических ожиданий вектора  ;
;
– координат  и
и 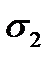 вектора
вектора 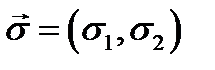 , называемого вектором средних квадратических отклонений вектора
, называемого вектором средних квадратических отклонений вектора  ;
;
– числа 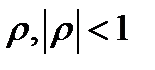 , называемого коэффициентом корреляции случайных величин
, называемого коэффициентом корреляции случайных величин 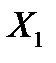 и
и 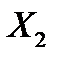 .
.
№17. Условные вероятности и плотности вероятностей. Независимость случайных величин.
Условным законом распределения случайной величины, входящей в систему, называется её закон распределения, вычисленный при условии, что другая случайная величина приняла определённое значение.
Условные функции распределения случайных величин  и
и 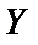 , входящих в систему, обозначаются
, входящих в систему, обозначаются 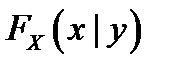 и
и 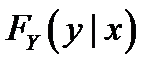 , а условные плотности распределения –
, а условные плотности распределения –  и
и 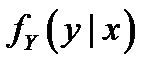 .
.
Теорема умножения плотностей распределения: 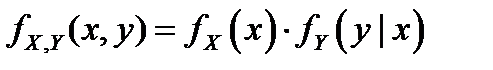 или
или 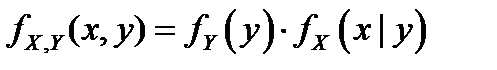 .
.
Для независимых случайных величин 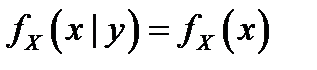 или
или 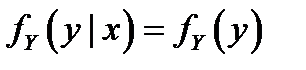 .
.
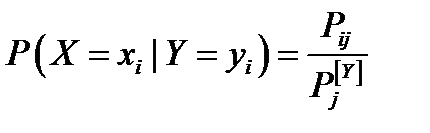 – условная вероятность.
– условная вероятность.
Случайные величины  и
и 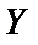 называют независимыми, если совместная функция распределения
называют независимыми, если совместная функция распределения 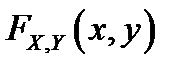 является произведением одномерных функций распределения
является произведением одномерных функций распределения 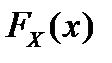 и
и 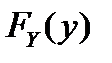 :
: 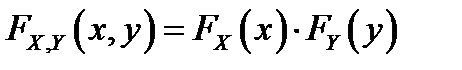 . В противном случае случайные величины называют зависимыми.
. В противном случае случайные величины называют зависимыми.
Для независимых случайных величин  и
и 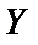 события
события 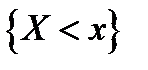 и
и 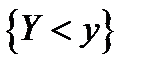 являются независимыми. Покажем, что независимыми являются и все события
являются независимыми. Покажем, что независимыми являются и все события 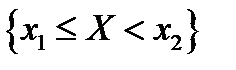 и
и 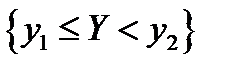 . Действительно, в силу независимости
. Действительно, в силу независимости  и
и 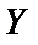 , свойства 5 двумерной функции распределения (
, свойства 5 двумерной функции распределения ( 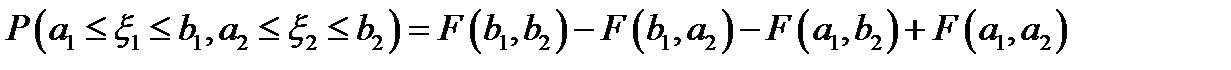 ) и свойства 3 одномерной функции распределения (
) и свойства 3 одномерной функции распределения ( 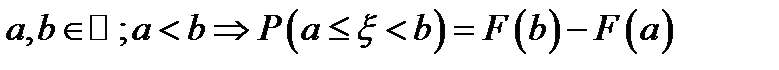 ) имеем
) имеем 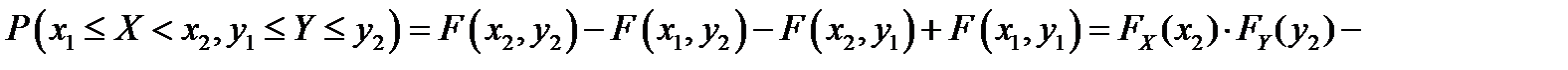
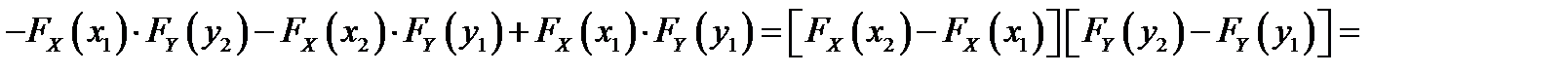
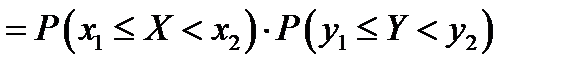 , что и означает независимость событий
, что и означает независимость событий 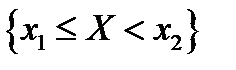 и
и 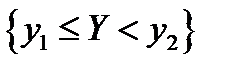 .
.
Теорема: Для того, чтобы непрерывные случайные величины  и
и 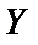 были независимыми, необходимо и достаточно, чтобы для всех
были независимыми, необходимо и достаточно, чтобы для всех 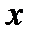 и
и 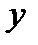
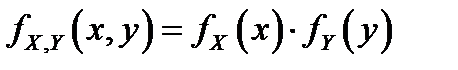 .
.
Доказательство: I. Необходимость. Пусть случайные величины  и
и 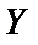 независимы. Тогда, согласно определению
независимы. Тогда, согласно определению 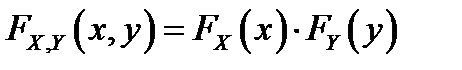 . Имеем:
. Имеем: 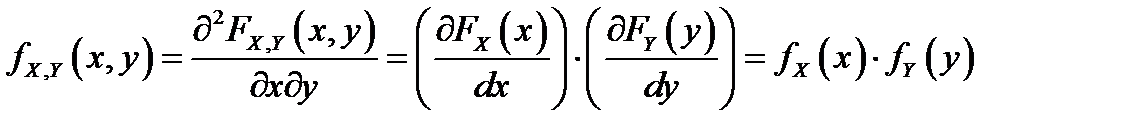 .
.
II. Достаточность. 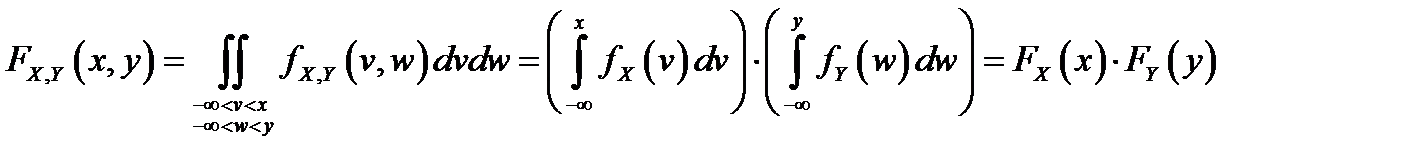 . Теорема доказана.
. Теорема доказана.
Теорема: Дискретные случайные величины  и
и 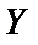 являются независимыми тогда и только тогда, когда для всех возможных значений
являются независимыми тогда и только тогда, когда для всех возможных значений 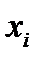 и
и 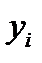
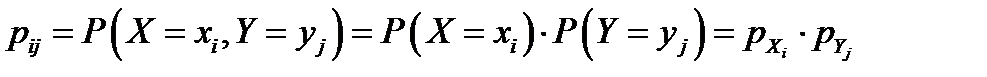 .
.
Случайные величины 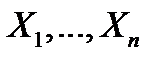 , заданные на одном и том же вероятностном пространстве, называют независимыми в совокупности, если
, заданные на одном и том же вероятностном пространстве, называют независимыми в совокупности, если 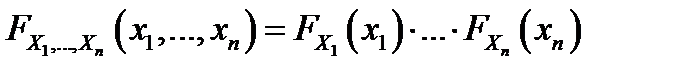 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|