
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№14. Основные законы распределения: нормальный, равномерный, биномиальный, показательный, Пуассона.
№14. Основные законы распределения: нормальный, равномерный, биномиальный, показательный, Пуассона.
1. Нормальный закон (для НСВ).
Случайная величина распределена по нормальному (или гауссову) закону, или имеет нормальное (гауссово) распределение, если её плотность  . Нормальное распределение зависит от двух параметров:
. Нормальное распределение зависит от двух параметров: 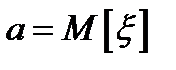 и среднего квадратического отклонения
и среднего квадратического отклонения  ,
, 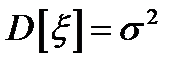 .
.
2. Равномерный закон (для НСВ).
Случайная величина имеет равномерное распределение на отрезке 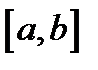 , если её плотность распределения
, если её плотность распределения 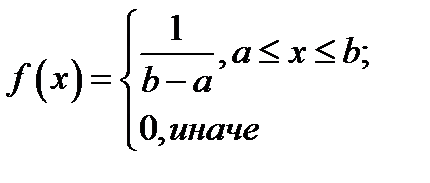 . В данном случае
. В данном случае 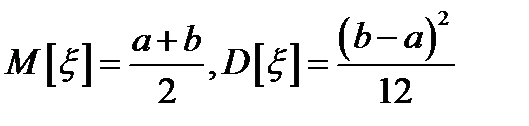 .
.
3. Биномиальный закон (для ДСВ).
Дискретная случайная величина 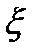 распределена по биномиальному закону, если она принимает значения
распределена по биномиальному закону, если она принимает значения 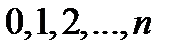 в соответствии с распределением, заданным формулой
в соответствии с распределением, заданным формулой 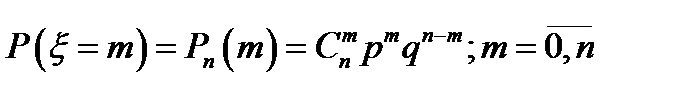 . Здесь
. Здесь 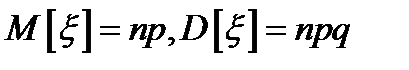 .
.
4. Показательный закон (для НСВ).
Случайная величина распределена по показательному (экспоненциальному) закону, если она имеет плотность распределения 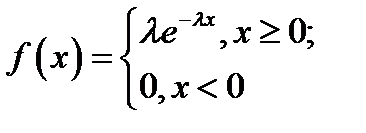 , где
, где 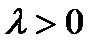 – параметр экспоненциального распределения;
– параметр экспоненциального распределения; 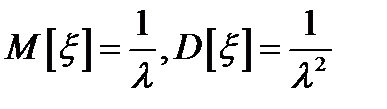 .
.
5. Закон Пуассона (для ДСВ).
ДСВ 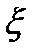 распределена по закону Пуассона, если она принимает целые неотрицательные значения с вероятностями
распределена по закону Пуассона, если она принимает целые неотрицательные значения с вероятностями 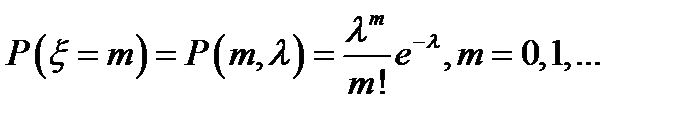 ;
; 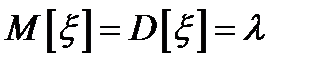 .
.
№15. Векторный случайные величины, совместная плотность, многомерная вероятность, многомерный ряд распределения.
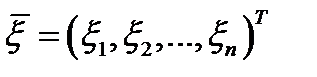 –многомерная случайная величина (упорядоченная совокупность случайных величин). Пример – абсцисса и ордината при случайном попадании (двумерная случайная величина).
–многомерная случайная величина (упорядоченная совокупность случайных величин). Пример – абсцисса и ордината при случайном попадании (двумерная случайная величина).
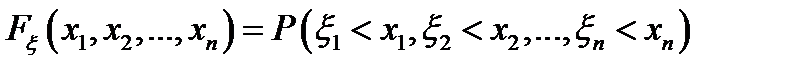 – функция распределения (совместная,
– функция распределения (совместная, 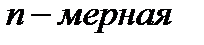 функция распределения),
функция распределения), 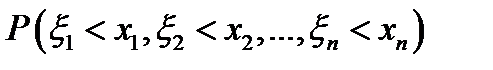 – многомерная вероятность.
– многомерная вероятность.
Рассмотрим свойства двумерной функции распределения:
1. 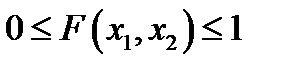 ;
;
2. 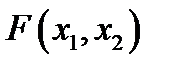 – неубывающая функция по каждому из аргументов
– неубывающая функция по каждому из аргументов 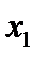 и
и 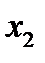 ;
;
3. 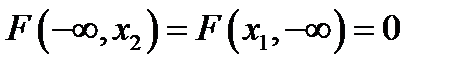 ;
;
4. 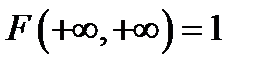 ;
;
5. 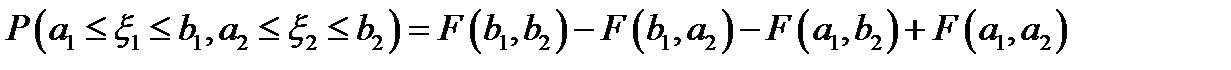 ;
;
6. 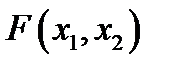 – непрерывная слева в любой точке
– непрерывная слева в любой точке 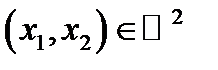 по каждому из аргументов
по каждому из аргументов 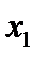 и
и 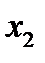 функция;
функция;
7. 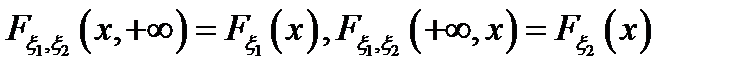 .
.
Совместная плотность распределения.
Непрерывной двумерной случайной величиной 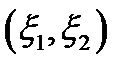 называют такую двумерную случайную величину
называют такую двумерную случайную величину 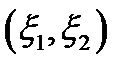 , совместную функцию распределения
, совместную функцию распределения 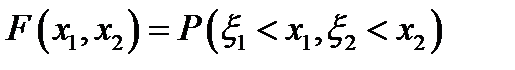 которой можно представить в виде сходящегося несобственного интеграла:
которой можно представить в виде сходящегося несобственного интеграла: 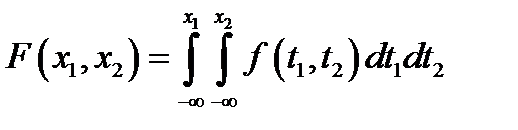 . Функцию
. Функцию 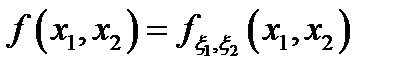 называют совместной двумерной плотностью распределения случайных величин
называют совместной двумерной плотностью распределения случайных величин 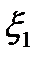 и
и 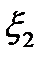 , или плотностью распределения случайного вектора
, или плотностью распределения случайного вектора 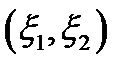 . Представление в виде повторного интеграла:
. Представление в виде повторного интеграла: 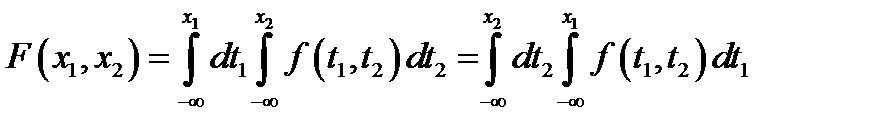 .
.
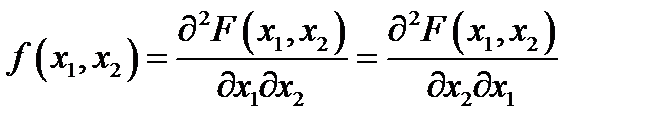
Свойства двумерной плотности распределения:
1. 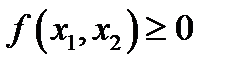 ;
;
2. 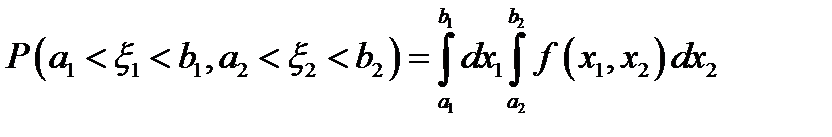 ;
;
3. 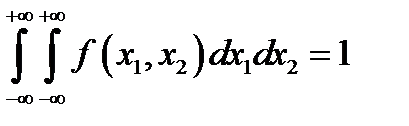 – условие нормировки;
– условие нормировки;
4. 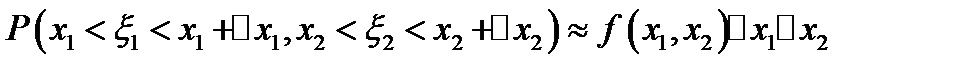 ;
;
5. 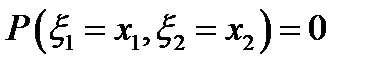 ;
;
6. 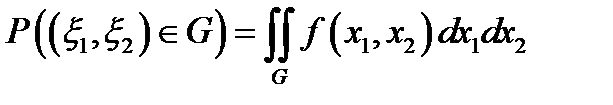 ;
;
7. 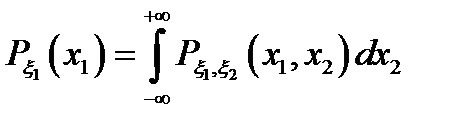 ;
;
8. 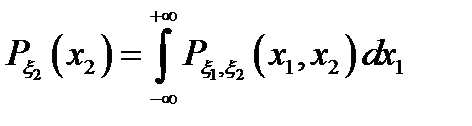 .
.
Многомерный ряд распределения.
Двумерную случайную величину 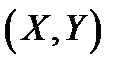 называют дискретной, если каждая из случайных величин
называют дискретной, если каждая из случайных величин 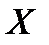 и
и 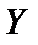 является дискретной.
является дискретной.
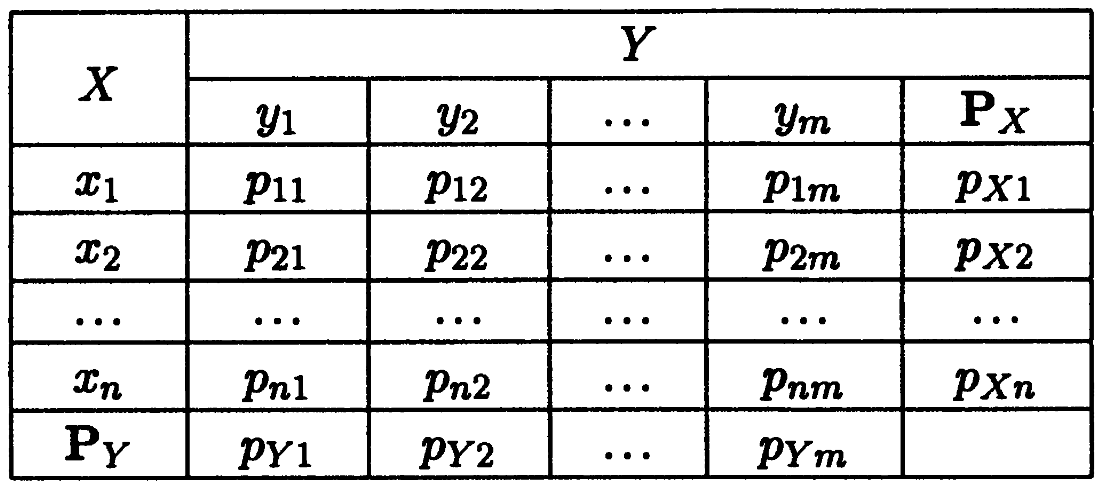 Для простоты ограничимся конечным множеством возможных значений, когда случайная величина
Для простоты ограничимся конечным множеством возможных значений, когда случайная величина 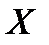 может принимать только значения
может принимать только значения 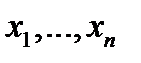 ,
, 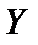 – значения
– значения 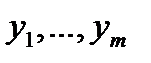 , а координаты двумерного случайного вектора
, а координаты двумерного случайного вектора 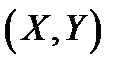 – пары значений
– пары значений 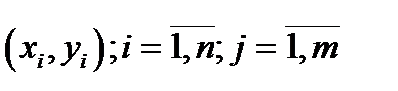 . Такое перечисление удобно представлять в виде таблицы. В этой таблице в верхней строке перечислены все возможные значения
. Такое перечисление удобно представлять в виде таблицы. В этой таблице в верхней строке перечислены все возможные значения 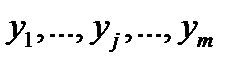 случайной величины
случайной величины 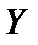 , а в левом столбце – значения
, а в левом столбце – значения 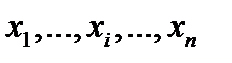 случайной величины
случайной величины 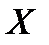 . На пересечении столбца «
. На пересечении столбца « 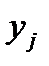 » со строкой «
» со строкой « 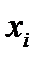 » находится вероятность
» находится вероятность 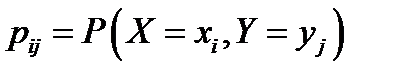 . В этой таблице обычно добавляют ещё одну строку «
. В этой таблице обычно добавляют ещё одну строку « 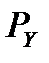 » и столбец «
» и столбец « 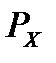 ». На пересечении столбца
». На пересечении столбца 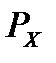 со строкой «
со строкой « 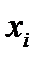 » записывают число
» записывают число 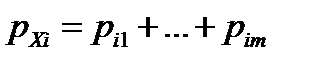 . Но
. Но 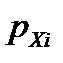 представляет собой не что иное, как вероятность того, что случайная величина
представляет собой не что иное, как вероятность того, что случайная величина 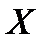 примет значение
примет значение 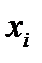 , т. е.
, т. е. 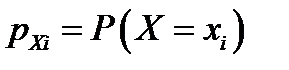 . Таким образом, первый и последний столбцы таблицы дают нам ряд распределения случайной величины
. Таким образом, первый и последний столбцы таблицы дают нам ряд распределения случайной величины 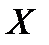 . Аналогично, в последней строке «
. Аналогично, в последней строке « 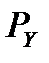 » помещены значения
» помещены значения 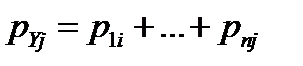 , а первая и последняя строки дают ряд распределения случайной величины
, а первая и последняя строки дают ряд распределения случайной величины 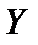 . Для контроля правильности составления таблицы рекомендуется просуммировать элементы последней строки и последнего столбца. Если хотя бы одна из этих сумм не будет равна единице, то при составлении таблицы была допущена ошибка.
. Для контроля правильности составления таблицы рекомендуется просуммировать элементы последней строки и последнего столбца. Если хотя бы одна из этих сумм не будет равна единице, то при составлении таблицы была допущена ошибка.
Используя данную таблицу, нетрудно определить совместную функцию распределения  . Ясно, что для этого необходимо просуммировать
. Ясно, что для этого необходимо просуммировать 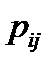 по всем тем
по всем тем 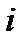 и
и 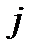 , для которых
, для которых 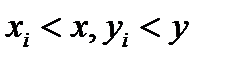 , т. е.
, т. е. 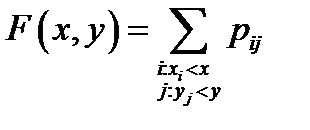 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|