
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№12. Математическое ожидание случайной величины и функции случайной величины. Свойства.
№12. Математическое ожидание случайной величины и функции случайной величины. Свойства.
Математическое ожидание случайной величины.
 – математическое ожидание (среднее значение случайной величины).
– математическое ожидание (среднее значение случайной величины).
Свойства математического ожидания:
1. 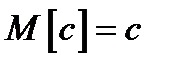 , где
, где 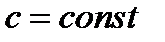 ;
;
2. 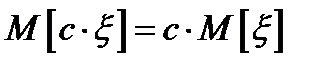 ;
;
3. 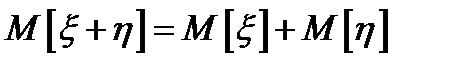 ;
;
4. 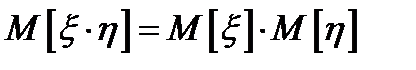 , если
, если 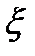 и
и 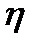 независимы.
независимы.
Функции случайной величины.
Пусть на вероятностном пространстве 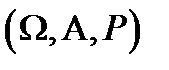 , где
, где 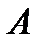 –
– 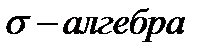 , задана случайная величина
, задана случайная величина 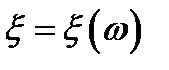 . Рассмотрим действительную функцию
. Рассмотрим действительную функцию 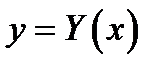 действительного аргумента
действительного аргумента 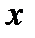 (область определения которой включает в себя множество возможных значений случайной величины
(область определения которой включает в себя множество возможных значений случайной величины  ).
).
Случайную величину 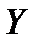 , которая каждому элементарному исходу
, которая каждому элементарному исходу 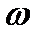 ставит в соответствие число
ставит в соответствие число 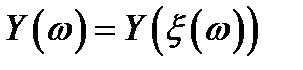 , называют функцией
, называют функцией 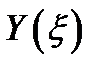 от скалярной случайной величины
от скалярной случайной величины 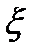 .
.
№13. Дисперсия и её свойства. Моменты случайной величины.
Дисперсия и её свойства.
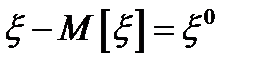 – центрированная случайная величина (отклонение
– центрированная случайная величина (отклонение 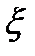 от
от 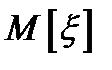 ),
), 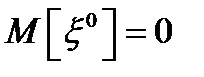 .
.
Дисперсией случайной величины 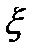 называется математическое ожидание квадрата отклонения
называется математическое ожидание квадрата отклонения 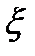 от
от 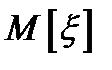 .
.
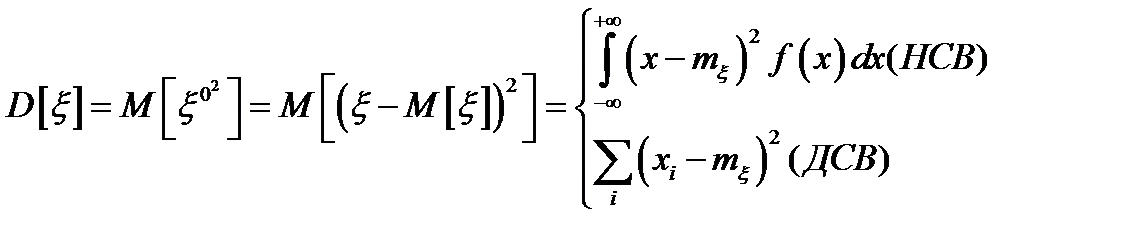
Свойства дисперсии:
1.  ;
;
2. 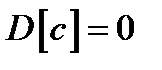 , где
, где 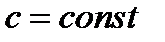 ;
;
3. 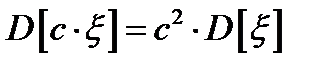 ;
;
4. 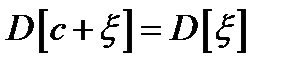 ;
;
5. 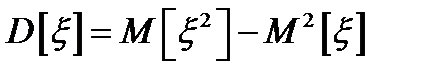
Доказательство: 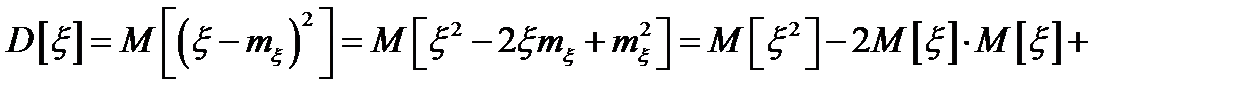
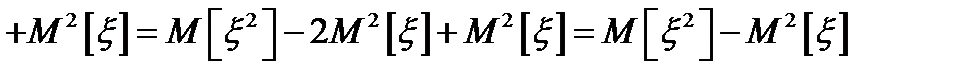 , ч. т. д.
, ч. т. д.
6. 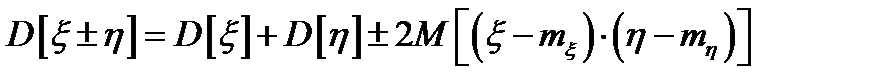 – ковариация (
– ковариация (  ,
, 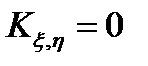 , когда
, когда 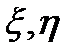 независимы).
независимы).
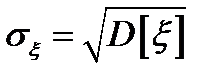 – среднее квадратичное (квадратическое отклонение) случайной величины
– среднее квадратичное (квадратическое отклонение) случайной величины 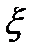 .
.
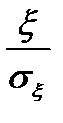 – нормированная случайная величина.
– нормированная случайная величина.

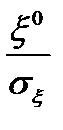 – стандартная случайная величина
– стандартная случайная величина 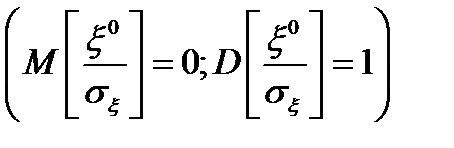 .
.
Моменты случайной величины.
Моментом 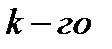 порядка случайной величины
порядка случайной величины 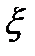 называется математическое ожидание величины
называется математическое ожидание величины 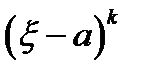 :
: 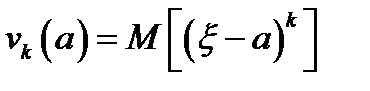 .
.
Если 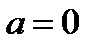 , то момент называется начальным. Легко видеть, что начальный момент первого порядка есть математическое ожидание величины
, то момент называется начальным. Легко видеть, что начальный момент первого порядка есть математическое ожидание величины 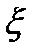 .
.
Если 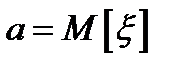 , то момент называется центральным. Легко видеть, что центральный момент первого порядка равен нулю, а центральный момент второго порядка есть не что иное, как дисперсия.
, то момент называется центральным. Легко видеть, что центральный момент первого порядка равен нулю, а центральный момент второго порядка есть не что иное, как дисперсия.
Начальные моменты будем обозначать буквой 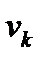 , а центральные – буквой
, а центральные – буквой 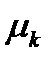 , указывая в обоих случаях нижним индексом порядок момента.
, указывая в обоих случаях нижним индексом порядок момента.
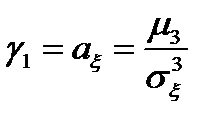 – коэффициент асимметрии.
– коэффициент асимметрии.
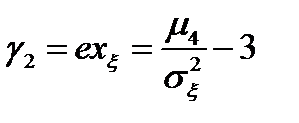 – коэффициент эксцесса.
– коэффициент эксцесса.
Мода для дискретного распределения – точка с максимальной вероятностью, а для непрерывного – точка максимума распределения (плотность в ней достигает максимального значения): 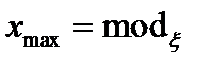 .
.
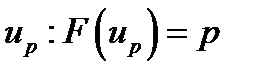 – квантиль распределения порядка
– квантиль распределения порядка 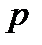 .
.
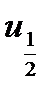 – медиана распределения.
– медиана распределения.
Для НСВ квантиль определяется однозначно. Для ДСВ понятие квантили не рассматривается. Вероятность попадания величины слева и справа от медианы одинакова:  .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|