- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№10. Дискретная случайная величина. Формы задания закона распределения дискретной случайной величины.
№10. Дискретная случайная величина. Формы задания закона распределения дискретной случайной величины.
Случайную величину 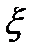 называют дискретной, если множество её возможных значений конечно или счётно.
называют дискретной, если множество её возможных значений конечно или счётно.
Формы задания закона распределения ДСВ:
1. Ряд распределения. 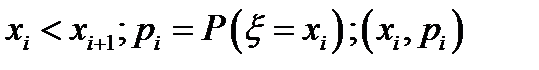
|
| 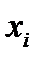
| 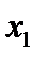
| 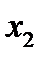
| 
| 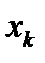
| 
|
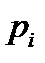
| 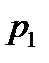
| 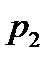
| 
| 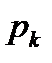
| 
|
Свойства ряда распределения:
1. 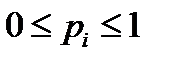 ;
;
2. 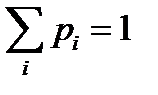 – свойство нормировки;
– свойство нормировки;
3. 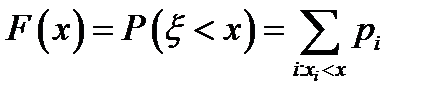 ;
;
4. 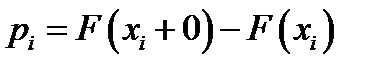
Доказательство: 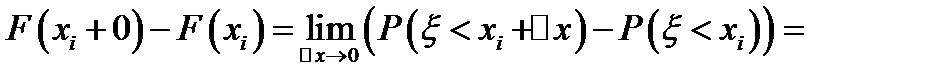
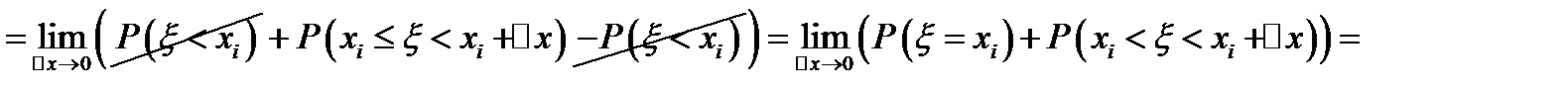
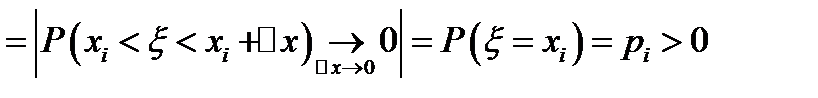 , ч. т. д.
, ч. т. д.
2. 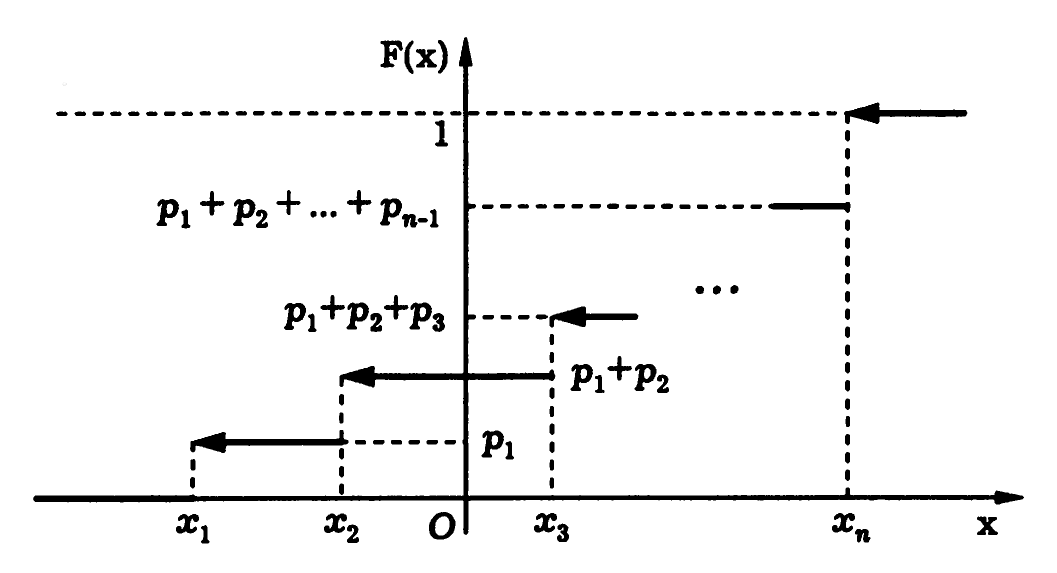 Функция распределения. Функция распределения ДСВ является кусочно постоянной функцией, принимающей на промежутке
Функция распределения. Функция распределения ДСВ является кусочно постоянной функцией, принимающей на промежутке  значение 0, на промежутках
значение 0, на промежутках 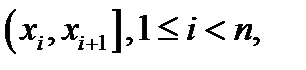 – значение
– значение 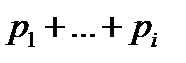 и на промежутке
и на промежутке 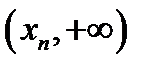 – значение 1.
– значение 1.
3. 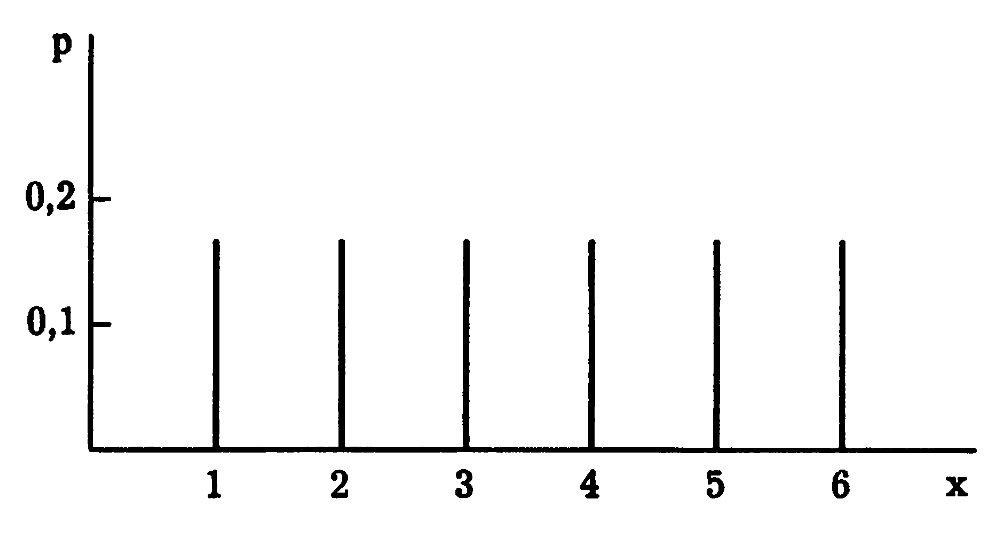 Аналитическое и графическое задание закона распределения ДСВ. Для задания закона распределения ДСВ, наряду с рядом распределения и функцией распределения, используют другие способы. Например, распределение игральной кости описывают формулой
Аналитическое и графическое задание закона распределения ДСВ. Для задания закона распределения ДСВ, наряду с рядом распределения и функцией распределения, используют другие способы. Например, распределение игральной кости описывают формулой 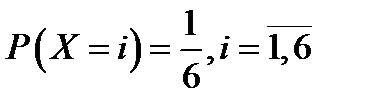 . Графическое изображение этого распределения приведено на рисунке.
. Графическое изображение этого распределения приведено на рисунке.
№11. Непрерывная случайная величина. Плотность вероятности и её свойства.
Непрерывной называют случайную величину 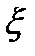 , функцию распределения
, функцию распределения 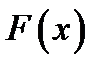 которой можно представить в виде
которой можно представить в виде 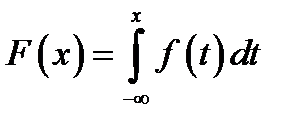 (1). Функцию
(1). Функцию 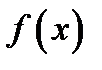 называют плотностью распределения случайной величины
называют плотностью распределения случайной величины 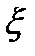 . Предполагают, что несобственный интеграл в представлении (1) сходится.
. Предполагают, что несобственный интеграл в представлении (1) сходится.
Все реально встречающиеся плотности распределения случайных величин являются непрерывными (за исключением, быть может, конечного числа точек) функциями. Следовательно, функция распределения для непрерывной случайной величины является непрерывной на всей числовой оси, и в точках непрерывности плотности распределения 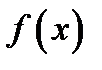 имеет место равенство:
имеет место равенство: 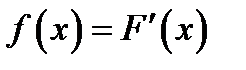 (2).
(2).
Соотношения (1) и (2), связывающие между собой функцию и плотность распределения, делают понятной следующую терминологию, часто употребляемую на практике. Функцию распределения 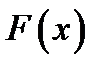 называют интегральным законом распределения случайной величины, а плотность распределения
называют интегральным законом распределения случайной величины, а плотность распределения 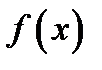 – дифференциальным законом распределения той же случайной величины.
– дифференциальным законом распределения той же случайной величины.
Плотность распределения обладает следующими свойствами:
1. 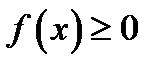 ;
;
2. 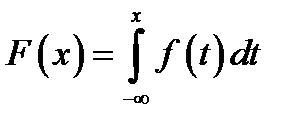
Доказательство: 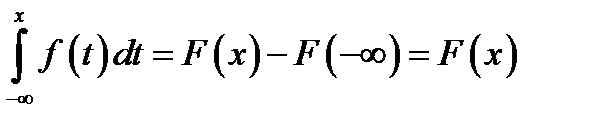 .
.
3. 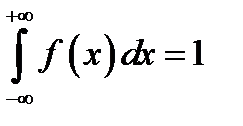 – свойство нормировки;
– свойство нормировки;
4. 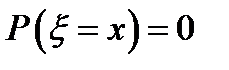 ;
;
5. 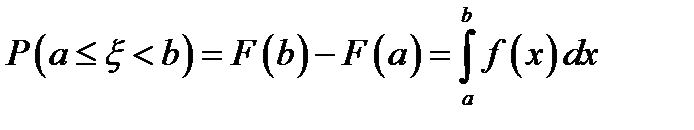 ; (равенство в записи
; (равенство в записи 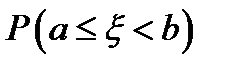 не играет никакой роли, т. к. вероятность попадания в точку равна нулю)
не играет никакой роли, т. к. вероятность попадания в точку равна нулю)
6. 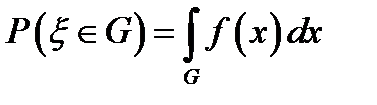 , где
, где 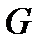 – некоторое множество (совокупность отрезков).
– некоторое множество (совокупность отрезков).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|