
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№9. Случайная величина. Функция распределения случайной величины и её свойства.
Скалярная случайная величина принимает значения из некоторого множества, до опыта заранее не известные.
Примеры случайных величин: количество студентов на занятии, уровень воды в реке, сила электрического тока в сети в конкретный момент времени, количество частиц в пригоршне песка и т. п.
В зависимости от множества принимаемых значений случайные величины подразделяются на непрерывные (НСВ) и дискретные (ДСВ).
У дискретной случайной величины множество значений конечно, либо счётно. Если множество значений несчётно, то случайная величина является непрерывной. Также различают смешанные случайные величины.
Случайные величины обозначаются:  .
.
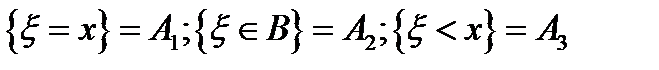 – случайные события, у которых можно считать вероятность.
– случайные события, у которых можно считать вероятность.
Малыми латинскими буквами обозначаются конкретные значения случайной величины.
Закон распределения случайной величины: 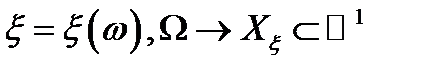 .
. 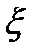 – измеримая функция, действующая из
– измеримая функция, действующая из  в подмножество
в подмножество  пространства
пространства  .
.  – множество значений случайной величины
– множество значений случайной величины 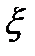 .
.
Измеримость функции  позволяет любому бореевскому множеству
позволяет любому бореевскому множеству
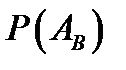
|
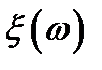
|

|
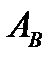
|
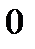
|
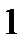
|

|
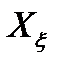
|
 поставить в соответствие одно конкретное множество
поставить в соответствие одно конкретное множество 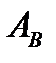 из
из  . Таким образом
. Таким образом 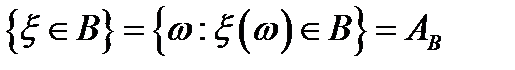 , поэтому вероятность события
, поэтому вероятность события  есть вероятность события
есть вероятность события 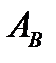 :
:  . Закон распределения – связь между подмножеством значений случайной величины и вероятностью её попадания в это подмножество.
. Закон распределения – связь между подмножеством значений случайной величины и вероятностью её попадания в это подмножество.
Случайная величина считается заданной, если задан её закон распределения и множество значений.
Вид функции  полностью задаёт закон распределения.
полностью задаёт закон распределения.
Как правило в практических задачах явный вид функции  неизвестен. Его либо невозможно, либо крайне трудно найти.
неизвестен. Его либо невозможно, либо крайне трудно найти.
Если 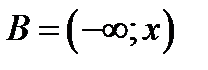 , то имеем вероятность
, то имеем вероятность  – функция распределения.
– функция распределения.  полностью задаёт закон распределения.
полностью задаёт закон распределения.
Свойства функции распределения:
1.  ;
;
2. 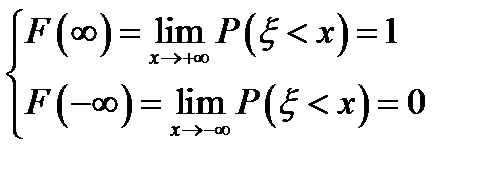 ;
;
3. 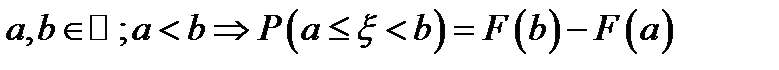
Доказательство: 
 , ч. т. д.
, ч. т. д.
4.  ;
;
5. 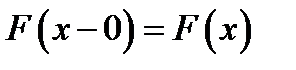
Доказательство: 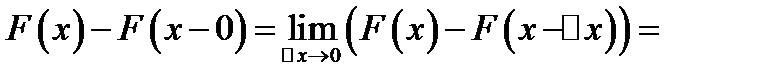
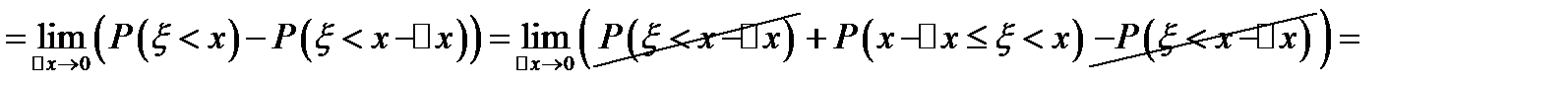
 , ч. т. д.
, ч. т. д.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|