
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№8. Схема независимых испытаний Бернулли. Теорема Пуассона. Предельная теорема Муавра-Лапласа.
Схема независимых испытаний Бернулли.
Рассматривается 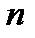 независимых испытаний, в каждом из которых событие
независимых испытаний, в каждом из которых событие 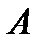 может произойти с вероятностью
может произойти с вероятностью 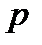 и не произойти с вероятностью
и не произойти с вероятностью 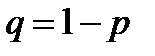 (
( 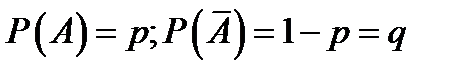 ).
).
Теорема: Вероятность 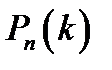 того, что в
того, что в 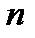 испытаниях по схеме Бернулли произойдёт ровно
испытаниях по схеме Бернулли произойдёт ровно 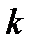 успехов, определяется формулой Бернулли
успехов, определяется формулой Бернулли 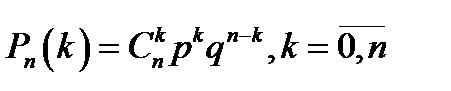 .
.
Доказательство: Результат каждого опыта можно записать в виде последовательности УНН…У, состоящей из 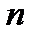 букв «У» и «Н», причём буква «У» на
букв «У» и «Н», причём буква «У» на 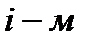 месте означает, что в
месте означает, что в 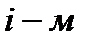 испытании произошёл успех, а «Н» – неудача. Пространство элементарных исходов
испытании произошёл успех, а «Н» – неудача. Пространство элементарных исходов  состоит из
состоит из 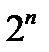 исходов, каждый из которых отождествляется с определённой последовательностью УНН…У.
исходов, каждый из которых отождествляется с определённой последовательностью УНН…У.
Каждому элементарному исходу 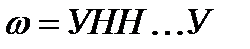 можно поставить в соответствие вероятность
можно поставить в соответствие вероятность 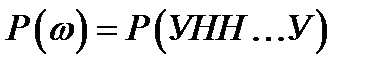 .
.
В силу независимости испытаний события У, Н, Н, …, У являются независимыми в совокупности, и потому по теореме умножения вероятностей имеем 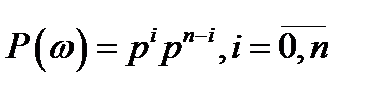 , если в
, если в 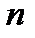 испытаниях успех «У» имел место
испытаниях успех «У» имел место 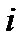 раз, а неуспех «Н», следовательно,
раз, а неуспех «Н», следовательно, 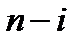 раз.
раз.
Событие 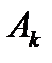 происходит всякий раз, когда реализуется элементарный исход
происходит всякий раз, когда реализуется элементарный исход 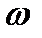 , в котором
, в котором 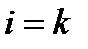 . Вероятность любого такого элементарного исхода равна
. Вероятность любого такого элементарного исхода равна 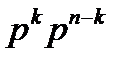 .
.
Число таких исходов совпадает с числом способов, которыми можно расставить 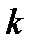 букв «У» на
букв «У» на 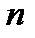 местах, не учитывая порядок, в котором их расставляют. Число таких способов равно
местах, не учитывая порядок, в котором их расставляют. Число таких способов равно 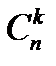 .
.
Так как 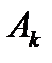 есть объединение (сумма) всех указанных элементарных исходов, то окончательно получаем для вероятности
есть объединение (сумма) всех указанных элементарных исходов, то окончательно получаем для вероятности 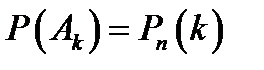 формулу Бернулли. Теорема доказана.
формулу Бернулли. Теорема доказана.
Из формулы Бернулли вытекают два следствия.
1. Вероятность появления успеха (события 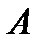 ) в
) в 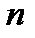 испытаниях не более
испытаниях не более 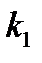 и не менее
и не менее 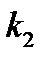 раз равна
раз равна 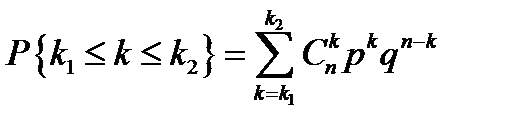 .
.
2. В частном случае при 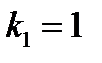 и
и 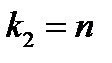 из предыдущей формулы получаем формулу для вычисления вероятности хотя бы одного успеха в
из предыдущей формулы получаем формулу для вычисления вероятности хотя бы одного успеха в 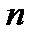 испытаниях:
испытаниях: 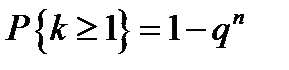 .
.
Теорема Пуассона.
Теорема: 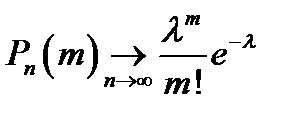 , где
, где 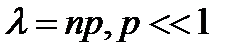 .
.
Доказательство: 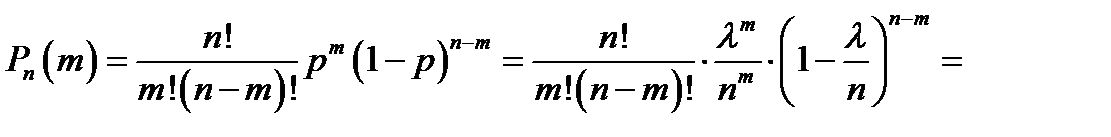
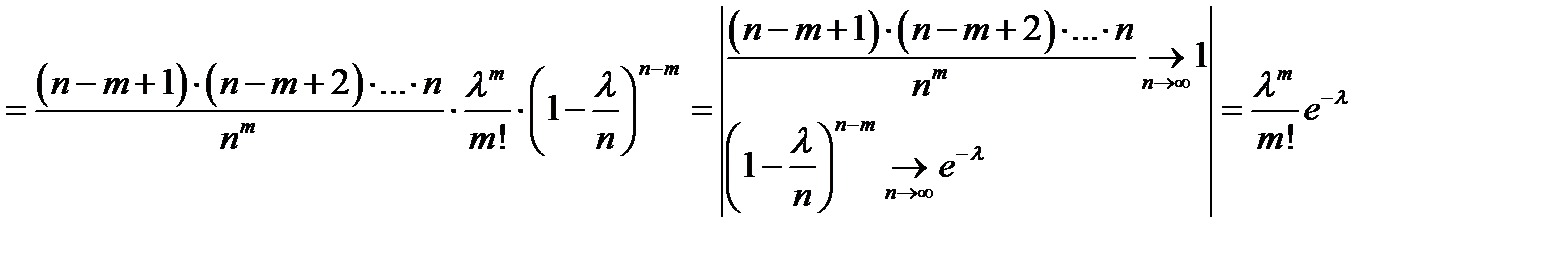 . Теорема доказана.
. Теорема доказана.
Предельная теорема Муавра-Лапласа.
Теорема: 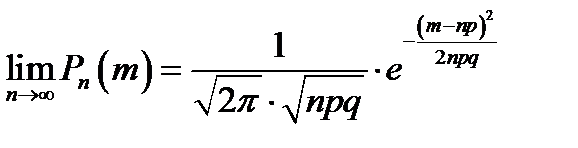 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|