№7. Формула полной вероятности и формула Байеса. Примеры.

Формула полной вероятности.

Рассмотрим группу несовместных событий 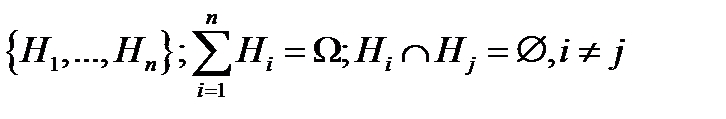. Эти события назовём гипотезами. Событие 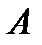может произойти или нет в том же опыте, что и 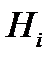. Т. к. 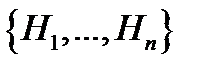– полная группа, то 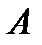произойдёт с одной и только одной из гипотез 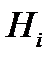вместе.

Теорема: Пусть для некоторого события 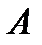и гипотез 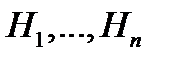известны 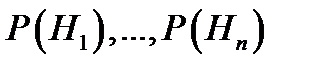и 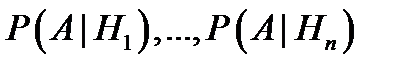. Тогда безусловную вероятность 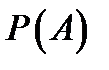определяют по формуле: 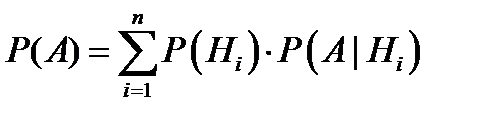– формула полной вероятности (ФПВ).

Доказательство: 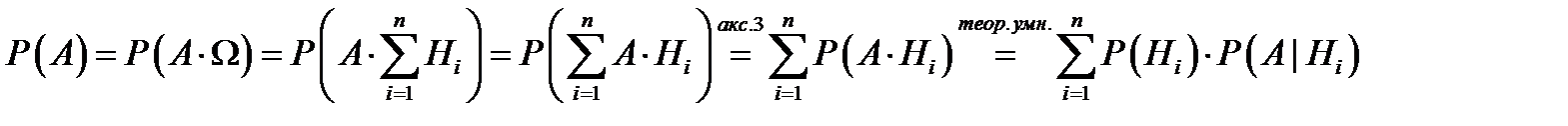. Теорема доказана.

Пример: Студент Иванов выучил все 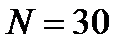экзаменационных билетов, но из них на «пять» – лишь 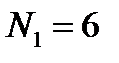. Определим, зависит или нет вероятность извлечения «счастливого» билета (событие 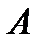) от того, первым или вторым выбирает Иванов свой билет.

Рассмотрим две ситуации.

Иванов выбирает билет первым. Тогда .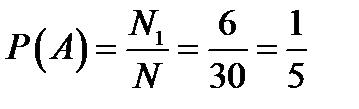

Иванов выбирает билет вторым. Введём гипотезы: 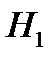– первый извлечённый билет оказался «счастливым», 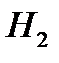– «несчастливым». Ясно, что 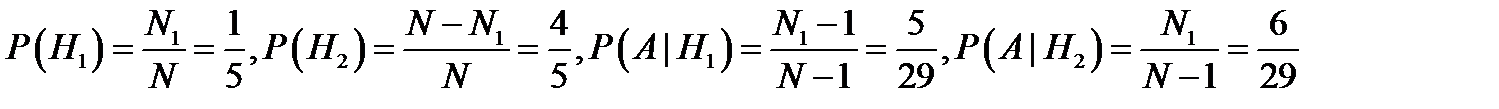. В силу формулы полной вероятности 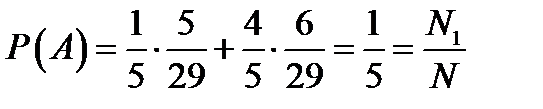, что совпадает с первой ситуацией.

Формула Байеса.

Пусть событие 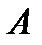произошло, тогда имеет место следующая теорема.

Теорема: Пусть для некоторого события 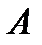и гипотез 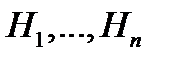известны 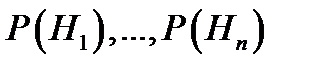и 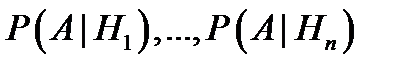. Тогда условная вероятность 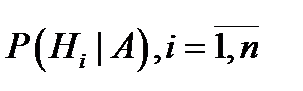, гипотезы 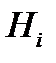при условии события 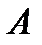определяется формулой Байеса .

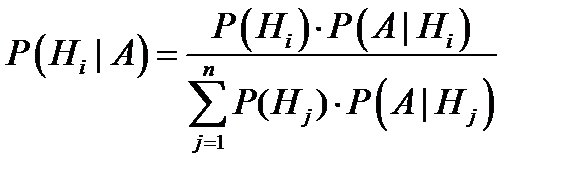Доказательство: 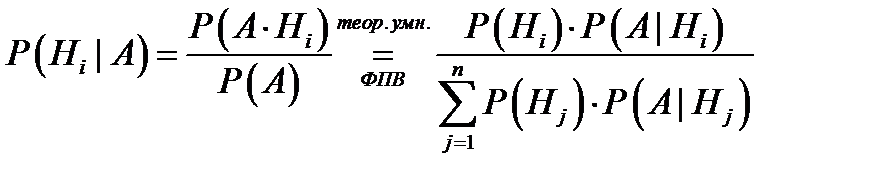. Теорема доказана.

Заметим, что вероятности 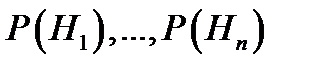обычно называют априорными (т. е. полученными «до опыта»), а условные вероятности 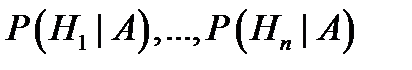– апостериорными (т. е. полученными «после опыта»).

Пример: врач после осмотра больного считает, что возможно одно из двух заболеваний, которые мы зашифруем номерами 1 и 2, причём степень своей уверенности в отношении правильности диагноза он оценивает как 40% и 60% соответственно. Для уточнения диагноза больного направляют на анализ, исход которого даёт положительную реакцию при заболевании 1 в 90% случаев и при заболевании 2 – в 20% случаев. Анализ дал положительную реакцию. Как изменится мнение врача после этого?

Обозначим через 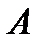событие, означающее, что анализ дал положительную реакцию. Естественно ввести следующие гипотезы: 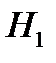– имеет место заболевание 1; 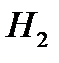– имеет место заболевание 2. Из условий задачи ясно, что априорные вероятности гипотез равны: 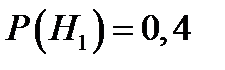и 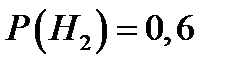, а условные вероятности события 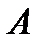при наличии гипотез 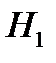и 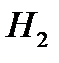равны 0, 9 и 0, 2 соответственно. Использую формулу Байеса, находим .

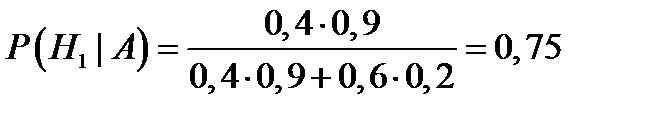Итак, врач с большей уверенностью признает наличие заболевания 1.

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒