
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№4. Теорема сложения. Следствия.
№4. Теорема сложения. Следствия.
Теорема: 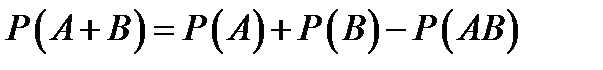 . Для
. Для 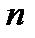 событий:
событий: 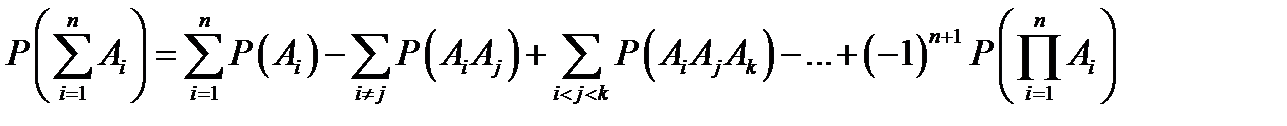 .
.

|
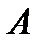
|
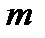
|
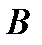
|
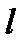
|
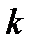
|
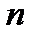
|
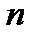 исходов.
исходов.
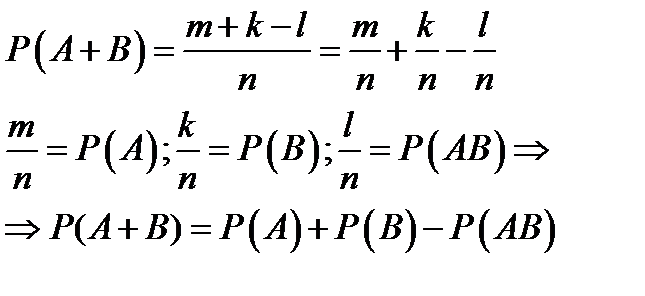
Теорема доказана.
Следствие 1: если 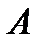 и
и 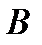 несовместны, то
несовместны, то 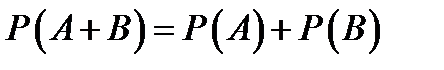 .
.
Следствие 2: 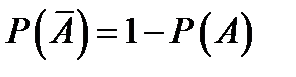
Доказательство: 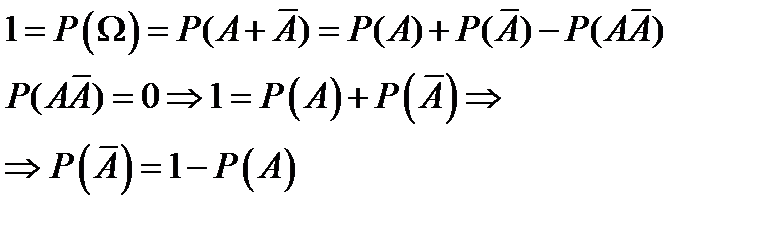
№5. Условная вероятность и её свойства. Теорема умножения вероятностей.
Говорят, что событие 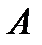 зависит от события
зависит от события 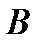 , если его вероятность меняется, когда происходит событие
, если его вероятность меняется, когда происходит событие 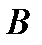 .
.
Условная вероятность – это вероятность события 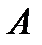 , подсчитанная при условии, что
, подсчитанная при условии, что 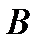 произошло. (
произошло. ( 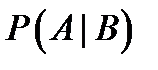 –
–  от
от 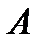 при условии
при условии 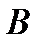 )
)
Если события 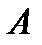 и
и 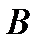 независимы, то
независимы, то 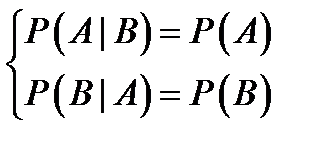 .
.
Теорема:
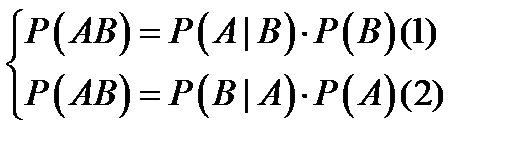 Для
Для 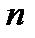 событий:
событий: 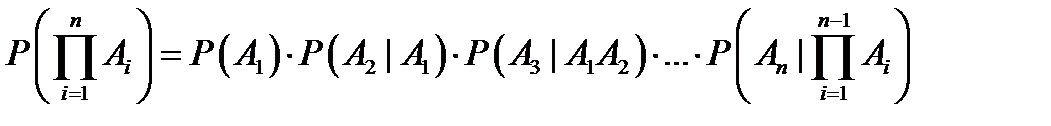 .
.

|
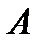
|
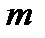
|
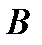
|
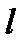
|
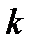
|
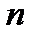
|
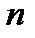 исходов.
исходов. 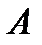 благоприятствуют
благоприятствуют 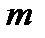 исходов,
исходов, 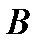 благоприятствуют
благоприятствуют 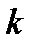 исходов,
исходов, 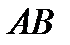 –
– 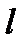 исходов. Пусть
исходов. Пусть 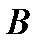 произошло, осталось
произошло, осталось 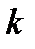 исходов,
исходов, 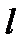 из них благоприятствуют
из них благоприятствуют 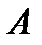 .
.
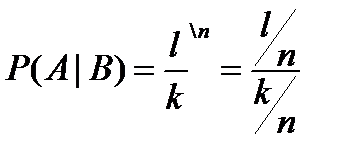
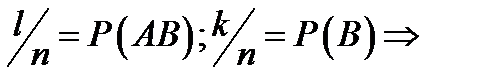
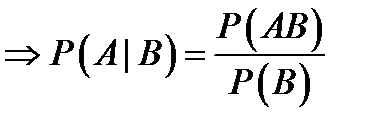 . Теорема доказана.
. Теорема доказана.
Следствие 1: если 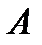 не зависит от
не зависит от 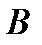 , то
, то 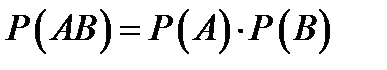 .
.
Следствие 2: если 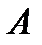 зависит от
зависит от 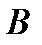 , то
, то 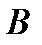 зависит от
зависит от 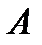 .
.
№6. Независимость событий и независимость испытаний.
События 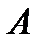 и
и 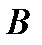 называются независимыми, если появление одного из них не меняет вероятности появления другого. Для независимых событий
называются независимыми, если появление одного из них не меняет вероятности появления другого. Для независимых событий
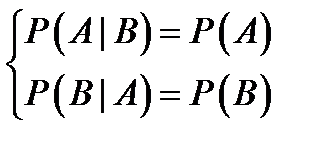 .
.
Свойство независимости событий взаимно, то есть если 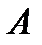 зависит от
зависит от 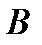 , то
, то 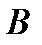 зависит от
зависит от 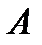 .
.
События 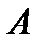 и
и 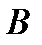 , имеющие ненулевую вероятность, являются независимыми тогда и только тогда, когда
, имеющие ненулевую вероятность, являются независимыми тогда и только тогда, когда 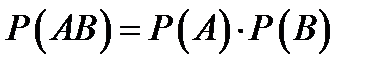 .
.
События 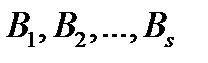 называются независимыми в совокупности, если для любого события
называются независимыми в совокупности, если для любого события 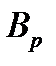 из их числа и произвольных
из их числа и произвольных 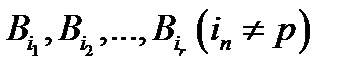 из их же числа события
из их же числа события 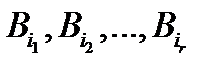 взаимно независимы. В силу теоремы умножения, это определение эквивалентно следующему: при любых
взаимно независимы. В силу теоремы умножения, это определение эквивалентно следующему: при любых 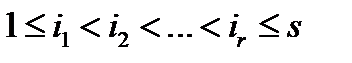 и
и 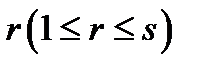
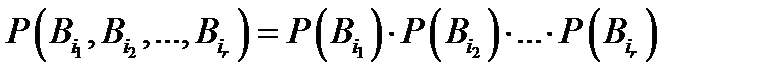 . Заметим, что для независимости в совокупности нескольких событий недостаточно их попарной независимости.
. Заметим, что для независимости в совокупности нескольких событий недостаточно их попарной независимости.
Рассмотрим опыт, состоящий в проведении двух испытаний. Эти испытания называются независимыми, если любые два события 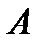 и
и 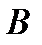 , из которых
, из которых 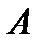 определяется по исходу первого испытания, а
определяется по исходу первого испытания, а 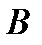 – по исходу второго, являются независимыми.
– по исходу второго, являются независимыми.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|