
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№2. Аксиоматическое определение вероятности. Аксиомы Колмогорова. Следствия.
№2. Аксиоматическое определение вероятности. Аксиомы Колмогорова. Следствия.
Пусть  – некоторое множество (множество элементарных исходов). Элементы будем обозначать
– некоторое множество (множество элементарных исходов). Элементы будем обозначать 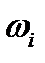 , подмножества
, подмножества 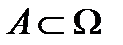 ,
, 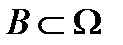 – случайные события.
– случайные события.
Рассмотрим 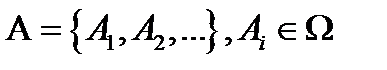 – алгебра множеств, порождённая подмножествами
– алгебра множеств, порождённая подмножествами  , если:
, если:
1. 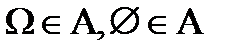 ;
;
2. 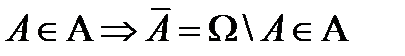 ;
;
3. 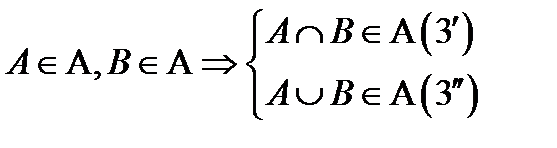 .
.
 –
– 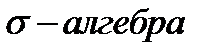 . Если условие 3 выполняется для произвольного количества множеств, то
. Если условие 3 выполняется для произвольного количества множеств, то 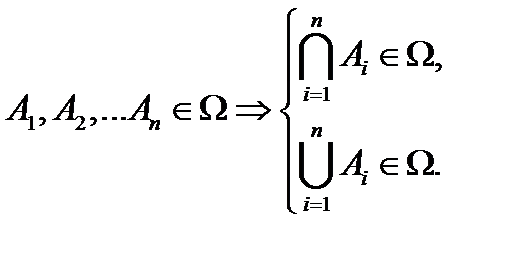
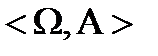 – измеримое пространство.
– измеримое пространство.
Аксиома 1(аксиома неотрицательности): Каждому элементу 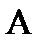 ставится в соответствие неотрицательное вещественное число
ставится в соответствие неотрицательное вещественное число 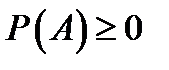 – вероятность.
– вероятность.
Аксиома 2 (аксиома нормированности): 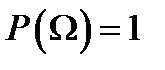 .
.
Аксиома 3(аксиома сложения): 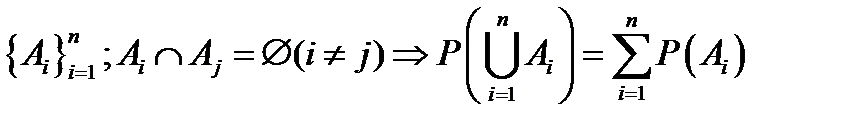 .
.
Аксиома 4(расширенная аксиома сложения): 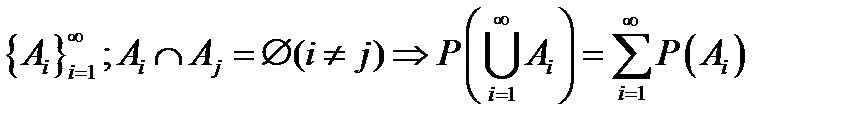 .
.
Аксиома 5 (аксиома непрерывности): 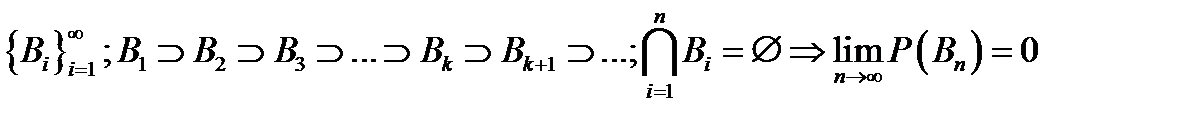 .
.
Следствие 1: 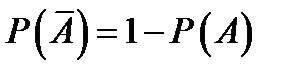 .
.
Доказательство: 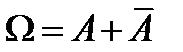 ,
, 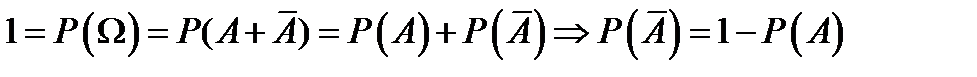 .
.
Следствие 2: 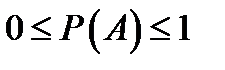 .
.
Доказательство: 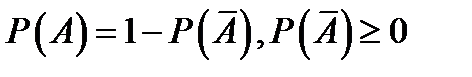 .
.
Следствие 3 (теорема сложения): 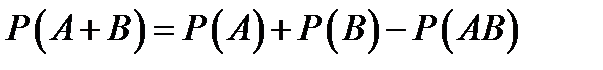 .
.
Доказательство: 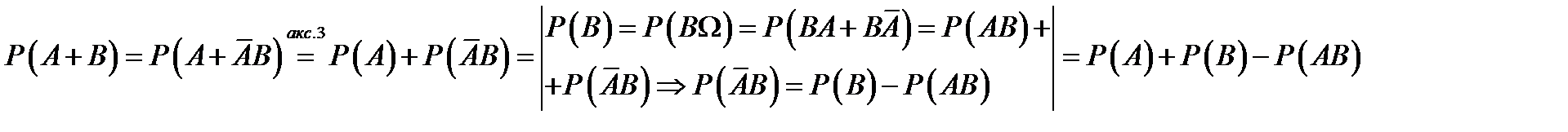 Следствие 4 (неравенство треугольника):
Следствие 4 (неравенство треугольника): 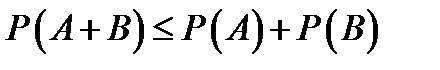 .
.
Следствие 5: 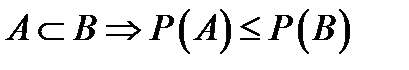 .
.
Доказательство: 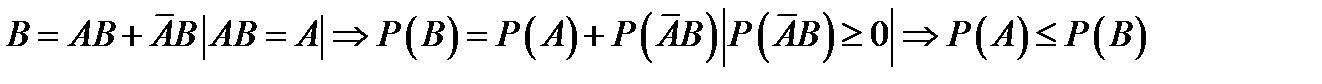 .
.
Следствие 6: 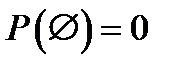 .
.
Доказательство: 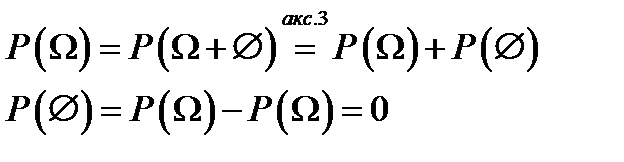 .
.
№3. Классическое, геометрическое и статистическое определения вероятности как частный случай аксиоматического.
Классическое определение вероятности.
Пусть всего 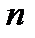 элементарных исходов,
элементарных исходов, 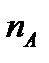 – число исходов, благоприятствующих событию
– число исходов, благоприятствующих событию 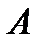 . Тогда
. Тогда 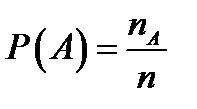 – вероятность.
– вероятность.
1. 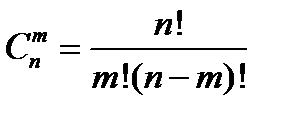 – число сочетаний. Если опыт состоит в выборе
– число сочетаний. Если опыт состоит в выборе 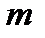 элементов из
элементов из 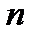 без упорядочения и без возвращения, то общее число элементарных исходов в опыте будет равно количеству различных
без упорядочения и без возвращения, то общее число элементарных исходов в опыте будет равно количеству различных  комбинаций, отличных друг от друга, по крайней мере, одним составом элементов.
комбинаций, отличных друг от друга, по крайней мере, одним составом элементов.
2. 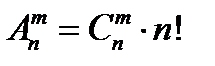 – число размещений без повторений. Если опыт состоит в выборе
– число размещений без повторений. Если опыт состоит в выборе 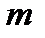 элементов из
элементов из 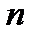 без возвращения, но с упорядочением элементов по мере их поступления, то количество элементарных исходов равно числу
без возвращения, но с упорядочением элементов по мере их поступления, то количество элементарных исходов равно числу  комбинаций, отличных друг от друга либо порядком следования элементов, либо их составом (но один и тот же элемент встречается в группе не более одного раза).
комбинаций, отличных друг от друга либо порядком следования элементов, либо их составом (но один и тот же элемент встречается в группе не более одного раза).
3. 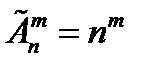 – число размещений с повторениями. Если опыт состоит в выборе
– число размещений с повторениями. Если опыт состоит в выборе 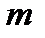 элементов из
элементов из 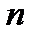 с возвращением и упорядочением элементов по мере их поступления, то общее число исходов опыта равно количеству
с возвращением и упорядочением элементов по мере их поступления, то общее число исходов опыта равно количеству  комбинаций, отличающихся друг от друга составом элементов, либо порядком их следования (при этом один и тот же элемент может повторяться несколько раз).
комбинаций, отличающихся друг от друга составом элементов, либо порядком их следования (при этом один и тот же элемент может повторяться несколько раз).
Геометрическое определение вероятности.
Если множество элементарных исходов может быть представлено некоторой областью 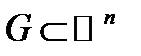 , а множество благоприятствующих событию
, а множество благоприятствующих событию 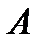 исходов – подобластью
исходов – подобластью 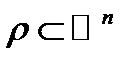 , то
, то 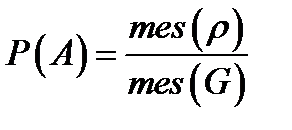 .
.
Статистическое определение вероятности.
Рассмотрим опыт, в котором событие 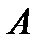 может появиться, а может и не появиться, и проведём этот опыт
может появиться, а может и не появиться, и проведём этот опыт 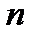 раз. Пусть
раз. Пусть 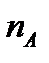 раз событие
раз событие 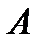 произошло, тогда
произошло, тогда 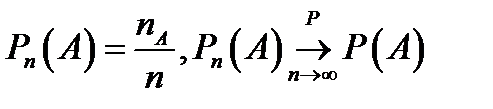 .
.
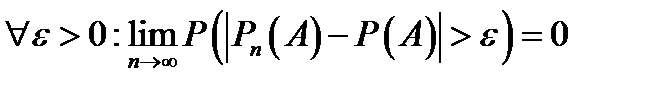 – сходимость по вероятности.
– сходимость по вероятности.
Вероятностью события 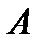 называют (эмпирический) предел
называют (эмпирический) предел 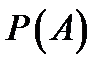 , к которому стремится частота
, к которому стремится частота 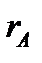 события
события 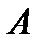 при неограниченном увеличении числа
при неограниченном увеличении числа 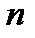 опытов.
опытов.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|