- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
j Универсальноеп/п учебное действие 7 страница
Планирование выполнения учебной задачи
Краткая справка
На первых этапах обучения в начальной школе для учащихся характерно
отсутствие действия планирования как целостной единицы деятельности.
Ученик способен выполнять отдельные операции, успешно копируя действия
учителя или другого ученика. Ученик более или менее отчетливо осознает
содержание отдельных «шагов», операционный состав действия планирова-
ния, может выполнять эти «шаги», рассказать о них или ответить на вопросы,
(например: «Что нужно сейчас сделать? А теперь что нужно делать? А как надо
это делать?»), однако не может делать это полностью самостоятельно. Не стоит
расстраиваться, если при этом ученик будет допускать ошибки. В этот период
он нуждается в развернутой и очень конкретной помощи на каждом этапе вы-
полнения задания. Эта работа нередко требует обращения к анализу образца,
повторного уточнения (раскрытия) каждой операции, их последовательности.
В дальнейшем намечать этапы работы ученик будет полностью самостоятель-
но, без помощи учителя.
Обучение планированию как универсальному регулятивному действию
требует усвоения детьми следующих операций: постановка цели предстоящей
деятельности как ее результата; продумывание «шагов», с помощью которых
можно получить результат; выстраивание последовательности выбранных
«шагов»; отражение последовательности решения учебной задачи в выбран-
ном словесном или графическом виде; высказывание предположения о том,
какие операции наиболее целесообразны для решения учебной задачи.
Методический комментарий
Начиная с первого класса, учителю важно предъявлять формулировки за-
даний, направленные на становление действия планирования:
♦ Составим план ...: с чего мы начнем, как будем действовать дальше?
♦ Расскажи, в какой последовательности нужно действовать...
♦ Расскажи порядок работы.
♦ Сможешь ли ты выполнить задание? Чего не хватает для выполнения?
♦ Согласны ли мы с Мишиным предложением о том, как он собирается
выполнить задание?
♦ Перед выполнением задания наметим план наших действий.
Для становления учебного действия «планирование выполнения учебной
задачи» необходимо задействовать возможности предметного содержания
обучения, которое требует определения последовательности предстоящих
шагов при построении алгоритма решения предметной задачи. Эта позиция
отмечена и в стандарте: «овладение основами... записи и выполнения алго-
ритмов; ... умение действовать в соответствии с алгоритмом и строить про-
стейшие алгоритмы» 42. Например, дети учатся составлять следующие алго-
42 Федеральный государственный образовательный стандарт начального общего образова-
ния.— М.: Просвещение, 2011. — С 11—12.
ритмы: правила порядка выполнения действий в числовых выражениях;
письменные вычисления (сложение и вычитание многозначных чисел, умно-
жение и деление многозначных чисел на однозначное и двузначное число);
решение текстовых задач; вычерчивание с помощью линейки отрезка задан-
ной длины; вычисление периметра и площади прямоугольника (квадрата)
и др.
Первая операция «постановка (принятие) цели предстоящей деятельно-
сти как ее результата» уже была подробно рассмотрена выше. Добавим, что
учителю важно стремиться к тому, чтобы на уроках учащиеся работали под
влиянием личностно принятой учебной цели «научиться...», «узнать ...», а само
принятие цели было мотивировано стремлением стать более умелым и знаю-
щим. Самостоятельную постановку учебной цели как личностно-значимой
учащиеся могут сформулировать так: «Буду учиться ..., потому что ...» или:
«Узнаю, какие действия и в какой последовательности нужно делать, что-
бы ... » или: «Научусь выполнять действия в этой последовательности».
Следующая операция — намечаю (продумываю) «шаги», с помощью кото-
рых можно получить результат. Ученику предлагается самостоятельно пред-
ставить перечень «шагов», с помощью которых можно получить результат:
Составь план: как ты будешь решать учебную задачу.
С чего начнешь?
Каким будет первый шаг?
Каким будет следующий шаг?
Как будешь действовать дальше?
Например, так выстраивается процесс моделирования звукового анализа
слова. Педагог в начале урока говорит: «Нам предстоит выполнить звуковой
анализ слова ...Расскажите мне, что нам нужно будет сделать, чтобы спра-
виться с этой задачей. Выслушиваются ответы детей, учитель их обобщает:
сначала мы будем произносить слово и одновременно продвигать указку
вдоль схемы слова. Потом мы ... (опять озвучивается мнение детей), будем
произносить слово с интонационным выделением первого звука на фоне все-
го слова, после этого ... и так далее. Пока первоклассникам трудно сделать это
все сразу самим в полном объеме, поэтому роль учителя заключается в удер-
живании единства проводимого учебного действия: обязательном прогова-
ривании уже проведенной операции и в стимулировании называния следую-
щей операции.
Следующие операции планирования: самостоятельное выстраивание
учеником последовательности выбранных «шагов»; отражение последова-
тельности решения учебной задачи в словесном или графическом виде. Цель
представленных операций — создание учащимся «образа» того пути, кото-
рый ему предстоит пройти. Эта работа включает самостоятельное составле-
ние, конструирование необходимой в данном конкретном случае последова-
тельности «шагов» в виде модели, схемы, словесного плана.
Например, сложение чисел 68 и 25 в ходе изучения темы «Письменное сло-
жение и вычитание чисел в пределах 100»:
1. Пишу единицы под единицами, десятки — под десятками.
2. Складываю единицы. Если при сложении единиц получено число боль-
ше 9, то единицы записываю под единицами, а один десяток
запоминаю.
3. Складываю десятки. Записываю результат под десятками. При сложе-
нии десятков нужно вспомнить, какое число десятков запоминали (1),
и к результату добавить еще один десяток: 6 дес. + 2 дес. = 8 дес.; 8 дес. +
1 дес. = 9 дес.
4. Записываю ответ. 93.
Такое поэлементное описание организует действия школьника, создает
условия для выстраивания последовательности «шагов» как при вычитании
двузначных чисел, так и при сложении (вычитании) трехзначных, а затем
и многозначных чисел.
Составление плана очень важно на уроках окружающего мира. Например,
уже первоклассникам можно предложить составить план наблюдений за рыб-
ками аквариума.
Сегодня,— говорит учитель,— мы будем рассматривать рыбок, живущих
в аквариуме. Как вы думаете, что нам нужно понаблюдать, чтобы составить рас-
сказ о жизни рыб. Дети предлагают рассмотреть внешний вид рыбки, способ пе-
редвижения и питания, особенности среды, в которой живут рыбы. Учитель
фиксирует пункты плана на доске: 1) внешний вид; 2) способ передвижения и т. д.
Следующая операция планирования — это высказывание предположения,
какие «шаги» наиболее целесообразны для решения учебной задачи. На опре-
деленном этапе обучения ученики готовы выбирать и объяснять «шаги», кото-
рые будут наиболее целесообразными (удачными, рациональными) для выпол-
нения задания. Но для этого учитель систематически предлагает им подобные
задания.
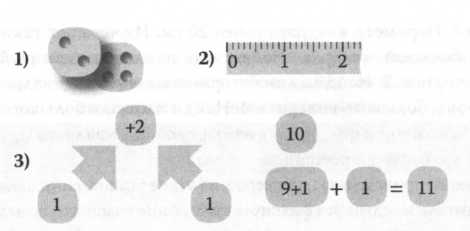
Например. На уроке математики в 1-м классе учитель предлагает выбрать,
какой из вариантов работы: 1), 2) или 3) можно считать наиболее рациональ-
ным для ответа на вопрос: «Как к 9 прибавить 2?».
|
|
Учащиеся объясняют, что они могут получить результат сложения, ис-
пользуя фишки (1), линейку (2); определяют, что эти «шаги» приводят к по-
лучению верного результата, но занимают много времени. После этого рас-
сматривают третий вариант: прибавление по частям и приходят к выводу,
что он более рациональный:
1. Представлю число 2 в виде суммы удобных слагаемых: это 1 + 1.
2. К числу 9 сначала прибавлю 1, чтобы получить 10.
3. К результату прибавлю единицу. Получаю ответ: число 11.
Далее учитель просит объяснить, какие «шаги» можно считать наи-
более целесообразными, если надо выполнить сложение: 8 + 3 =?; 7 + 4 =?;
9 + 5 =?.
Обратим внимание читателей, что о становлении планирования как
универсального учебного действия говорит тот факт, что ученик научился
самостоятельно осуществлять построение плана выполнения задания (ре-
шения учебной задачи), используя общие принципы, выстраивает конкрет-
ную, необходимую для решения данной задачи последовательность дей-
ствий. На протяжении всего процесса решения задачи ученик работает са-
мостоятельно, допущенные ошибки исправляет сам, демонстрирует уверен-
ные самостоятельные действия в определении последовательности дей-
ствий для решения как стандартных, так и нестандартных задач.
Пример 1. Расскажи порядок работы, если необходимо дописать пропу-
щенные числа.
|
|
Пример 2. Периметр квадрата равен 20 см. Из четырех таких квадратов
составили большой квадрат. Найди его площадь. Действуй по плану:
1. Нарисуй чертеж. 2. Найди длину стороны маленького квадрата. 3. Найди
длину стороны большого квадрата. 4. Найди площадь большого квадрата.
Подумай, можно ли по-другому найти площадь квадрата?
Запиши другой план решения этой задачи.
Как видно из приведенных примеров, на этапе становления любого учебного
действия учитель каждый раз фиксирует внимание учащихся на необходимости
планирования выполнения задания. Анализ практической работы учителей на-
чальных классов показывает, что не так часто на уроке ставятся дидактические
задачи, направленные на формирование у учащихся действия планирования.
В ФГОС НОО это учебное действие отмечено как важный метапредметный ре-
зультат обучения, и оно должно стать объектом особого внимания учителя.
Регулятивные универсальные учебные действия,
характеризующие прогнозирование
Краткая справка
Прогнозирование (от греч. prognosis — предвидение, предсказание, «зна-
ние наперед») — разработка прогнозов, то есть вероятных суждений, обосно-
ванных предположений о будущем состоянии того или иного явления, о кон-
кретных перспективах дальнейшего развития происходящего процесса, по-
могающее взглянуть в будущее и оценить последствия выбранного пути.
Авторитетное мнение
Как отмечает Л. А. Регуш, прогнозирование выступает как регулирую-
щая функция любого психического процесса.
Приступив к выполнению задания, ученик может строить прогноз об эф-
фективности осуществления определенных «шагов» для достижения цели.
«Возможность предвосхищения результата, возможность предварительно-
го, до ее выполнения, определения структуры деятельности, уровень анали-
за задания, учет всех требований условия задания, полнота использованной
для построения прогноза информации, содержащейся в задании, могут лечь
в основу суждений об уровне сформированности универсального учебного
действия прогнозирования»43.
Рассмотрим перечень операций, характеризующих прогнозирование как
регулятивное универсальное учебное действие.
43 Регуш Л. А. Психология прогнозирования: успехи в познании будущего.— СПб.: Речь,
2003.-352 с.
| Операциональная характеристика регулятивных
|
|
|
Определение возможности выполнения учебной задачи
Методический комментарий
Первое универсальное действие, связанное с прогнозированием, требует
усвоения детьми определенных операций (см. таблицу 5).
Очень важно организовать этап предварительного (контрольного) про-
гноза. Цель его: учить детей предсказывать результат деятельности, пред-
ставлять способ решения задачи, предвидеть трудности. В процессе учеб-
ного диалога высказываются предположения о возможных результатах дея-
тельности; осуществляется анализ набора предполагаемых операций.
Например, третьеклассники анализируют набор слов и словосочетаний
и высказывают предположение о том, какой рассказ можно составить на ос-
нове такого набора.
Девочка Маша; первоклассница, новое платье, белокурая, голубоглазая,
шустрая, красный бант, косички, кружевной воротничок, принцесса.
В случае необходимости можно напомнить детям, какие типы расска-
зов существуют (описание, повествование, рассуждение), вспомнить ха-
рактерные особенности каждого типа. Предложить ученикам проанализи-
ровать предложенные слова и словосочетания с точки зрения лексики.
В качестве своеобразной помощи дается задание: определить название
и тему рассказа. Учащиеся могут предложить разные варианты: «Как Маша
в школу собиралась», «Портрет девочки Маши», «Новое платье Маши».
В этом случае опять пригодится задание на прогнозирование того, что по-
лучится в результате. Оказывается, что для первого варианта не хватает
слов — не ясно, какие события происходят с Машей, когда она готовится
в школу. При третьем варианте остаются неиспользованными слова, кото-
рые никак не связаны с описанием нового платья. В результате делается
прогноз: целесообразно, чтобы рассказ назывался «Портрет Маши», в этом
случае все слова будут использованы, внешний вид девочки будет описан
полно и образно.
Целесообразно предлагать задания на анализ условий, предоставленных
для решения учебной задачи. Так, в задании имеется небольшая «провока-
ция», не устранив которую решить задачу нельзя. Это тоже относится к про-
гностическим умениям: представить возможное развитие операций по реше-
нию учебной задачи.
Например, второклассникам дается задание на проверку знаний о разных
классах животных: разделить животных на две группы: звери и рыбы. В пред-
лагаемых иллюстрациях изображение рыб отсутствует.
Учитель предлагает рассмотреть рисунки и ответить на вопросы: «Кто го-
тов выполнить задание и знает, что получит правильный результат?», «Можно
ли решить эту задачу?», «Почему нет? (почему да?)», «Все ли условия есть для
ее решения?», «Что нам необходимо, чтобы получить требуемый результат?».
На первый взгляд, кажется, что второклассники сразу обнаружат «подвох»
и скажут: «Эту задачу решить нельзя, не хватает данных — нет рисунков рыб».
Но такое предположение излишне оптимистично. Как показывает опыт, дети
пытаются выполнять задание без всякого прогноза получения результата:
они относят к рыбам зверей, «похожих» по месту обитания на рыб («живет
в море, значит рыба») — кита, дельфина, моржа. Такова психологическая осо-
бенность младших школьников — они уверены, что учитель не может дать
задание с ошибкой, не предупредив их об этом заранее.
Большие возможности предоставляет для создания ситуаций, требующих
определения возможности или невозможности выполнения учебной задачи,
математика. Учитель составляет текст задачи таким образом, чтобы какое-то
условие отсутствовало. И дети, еще не приступая к работе по решению зада-
чи, обсуждают возможность получения результата (строят прогноз): можно
ли при таких условиях его достичь? Какого условия нет?
Например. Прочитайте задачу и определите: можно ли ответить на во-
прос задачи.
«Учащиеся начальных классов собрались поехать на теплоходе. Из перво-
го класса поедут 10 человек, из второго столько же, а из четвертого на пять
человек больше, чем из первого. Сколько детей третьего класса поедет
на теплоходе?»
В случае затруднения учитель помогает учащимся построить прогноз:
«Что в условии говорится об учащихся третьего класса? Они поедут или
не поедут на теплоходе?» Об этом что-то сказано в тексте? Дети делают вывод:
результат получить нельзя, т. к. в тексте ничего не сказано о том, поедут ли
дети третьего класса на теплоходе.
Анализ подобных ситуаций позволяет подвести детей к осознанному вы-
воду: перед тем, как приступить к решению данной учебной задачи, нужно
«прикинуть» (предположить, быстро представить), достаточно ли условий
для ее выполнения, все ли условия верны, какие из них не нужны, а каких
не хватает и т. п.
Рассмотрим пример задания, в котором требуется еще до начала работы
подумать, какие группы могут быть выделены: «Выскажите предположение
о том, каким образом можно распределить записи 7 + 2, 12 - 3, 5 + 3,
10 - 2 по группам двумя разными способами». Ученик планирует, по какому
существенному признаку он может произвести группировку: выделение за-
писей сложения (7 + 2, 5 + 3) и вычитания (12 - 3,10 - 2); или записей с резуль-
татом 9 (7 + 2,12 - 3) и результатом 8 (5 + 3,10 - 2).
К 4-му классу задания усложняются, например: «Выскажите предполо-
жение о том, во сколько раз увеличили длину стороны квадратной клумбы,
если площадь этой клумбы увеличили в 4 раза, сохранив ее форму.
Проверьте свое предположение, выполнив рисунок от руки».
Вместе с тем, важно подводить учащихся к необходимости отвечать себе
на вопрос о возможности решения данной учебной задачи, то есть определе-
нию «границы» собственных знаний: различению ситуации «Это я знаю
и умею» / «Этого я пока не знаю и не умею». При определенных условиях уче-
ник осознает потребность, необходимость нового знания, способа действия,
одновременно идет уточнение, каких именно знаний/умений/способов дей-
ствия не хватает для выполнения учебного задания. В процессе учебного ди-
алога определяется путь поиска нужного знания/овладение «новым» спосо-
бом. Могу обратиться за помощью к взрослому или самостоятельно найти
нужное знание/овладеть способом, либо отказаться от выполнения.
Представляется целесообразным побуждать учащихся к высказываниям
в ситуациях спора, дискуссии, которые вызваны наличием некоторого про-
тиворечия. Для создания такого рода ситуаций учащимся предъявляются
задания, которые очень похожи на обычные задачи (задания), однако на са-
мом деле оказываются нерешаемыми, т. к. содержат некорректные данные:
Пример 1. В детский сад привезли 20 кг яблок и 8 пакетов винограда.
На сколько килограммов больше привезли яблок, чем
винограда?
Пример 2. Запиши к данным словам антонимы (слова, противополож-
ные по значению): радостный —__________ ; опасный —_________ ;
хвастливый —__________ ; капустный —__________ .
В первом примере задачу решить нельзя, т. к. данные имеют разные
единицы измерения (килограмм и пакет), что позволяет ученику уйти
от механического применения готового заученного алгоритма (20-8).
Во втором примере к слову «капустный» невозможно подобрать слово,
противоположное по значению и ученик должен поставить прочерк («нель-
зя записать»), обозначающий осознанный отказ от выполнения. Таким об-
разом, анализ предъявляемой учебной задачи, выяснение ее особенностей,
определение невозможности выполнить «нерешаемую» задачу — это необ-
ходимые «шаги», которые заставляют ученика обосновывать свои дей-
ствия («Почему в данном случае я поступаю именно так?»), положительно
влияют на выработку потребности объяснить каждый шаг решения, что
является важным аспектом в формировании универсального действия.
Задачи (задания) с избыточными, недостающими, а также некор-
ректными данными являются ценными для формирования этого учебного
действия. Решение таких задач не допускает действия по шаблону, застав-
ляет учащихся критически оценивать условие, из разной информации из-
влекать ту, которая непосредственно относится к поставленному вопросу.
До начала решения учебной задачи, нужно «оценить ситуацию», предпо-
ложить, быстро представить, достаточно ли условий для ее выполне-
ния, какие из них не нужны, а каких не хватает: самостоятельно обнару-
жить избыточную, недостающую или некорректную информацию, выя-
вить пути преобразования условия, позволяющего найти ответ на вопрос.
Предвидение возможных
трудностей, ошибок в работе
Пооперационный состав второго универсального действия, связанного
с прогнозированием, может быть представлен следующим образом: предполо-
жение (осознание) возникновения трудности при самостоятельном выполне-
нии; определение того, нужна или не нужна помощь учителя или однокласс-
ников («могу выполнить самостоятельно, без посторонней помощи»; «могу
выполнить только с помощью»); принятие решения о возможности или не-
возможности самостоятельного выполнения; формулирование просьбы о по-
мощи; планирование возможных шагов для преодоления трудностей.
Приведем пример осуществления этого действия. В третьем классе
учащиеся выполняют задание: «Поставь знаки действий и скобки между
числами так, чтобы получились верные равенства,
1)22 2 4 3 = 9 2) 22 2 4 3 = 11 3) 22 2 4 3 = 20».
Приступая к выполнению, третьеклассник анализирует условие, пони-
мает, что он должен оперировать числами только в пределах 100 (это лег-
ко), и может использовать все известные арифметические действия: сло-
жение, вычитание, умножение, деление; может ставить скобки. В то же
время, ученик осознает, предполагает, что его ожидают трудности при
самостоятельном выполнении: «Я не знаю, где и какие знаки поставить,
чтобы получить заданный результат». Помочь ученику принять решение
о возможности/невозможности самостоятельного выполнения могут сле-
дующие приемы, которые есть в арсенале учителя: 1) рассмотри вариант
одного из правильных решений (22 + 2): 4 + 3 = 9; 2) попробуй поставить
знаки сначала карандашом; 3) попробуйте сделать одно задание в паре
с соседом по парте и т. п.
Приведем пример по русскому языку. Выпиши две группы слов: 1) слова,
в которых безударные гласные можно проверить (сначала записывай прове-
рочные слова); 2) слова с непроверяемой гласной.
Для св... ей р... боты художник Ос... нь вз... ла самые яркие краски и прежде
всего отправилась с ними в лес. Там и прин... лась за св... ю к... ртину.
Б... резы и клены она покрыла лимонной ж... лтизной. А листья ... синок
разрумянила, будто спелые ябл... ки. Стал ... синник весь ярко-красный,
весь как ... гонь горит. (Г. Скребицкий)
Таким образом, отвечая самому себе на вопрос: «Какие трудности могут
встретиться?», ученик понимает, что есть набор возможных шагов, позволя-
ющих преодолеть эти трудности (попробуй поставить знаки сначала каран-
дашом; сначала записывай проверочные слова и др.) В итоге он приходит
к выводу: «не могу выполнить самостоятельно, прошу о помощи» или «пла-
нирую возможные шаги для преодоления трудности».
Регулятивные универсальные учебные действия,
характеризующие контроль и коррекцию
Краткая справка
Контроль учебной деятельности есть соотнесение предметного действия
с конкретными условиями его выполнения и с ожидаемыми результатами.
Контроль как учебное действие осуществляется и как проверка самим уче-
ником качества усвоения программного материала по конечному результа-
ту, и как действие активного прослеживания правильности выполнения
операций учебной задачи (в том числе и мыслительных), осуществляемое
по ходу ее решения.
Выделяют несколько видов контроля: итоговый, пооперационный, пла-
нирующий, упреждающий, рефлексивный, в каждом из этих видов просма-
тривается качество универсальности.
Итоговый контроль — это проверка результата решения учебной зада-
чи, которая осуществляется как ответ на вопрос, выполнено задание или
нет и насколько качественно.
Пооперационный контроль — это проверка процесса решения учебной
задачи, которая предполагает выяснение правильности операций, способов
по ходу их выполнения. Психологи считают, что пооперационный (поиско-
вый) контроль — это более высокий уровень контроля, чем итоговый. Его
особенность — в слежении за ходом действия, за тем, какая операция вы-
полняется в данный момент, предстоит ли корректировка деятельности.
Одновременно идет контроль качества: как выполняется действие, соответ-
ствуют ли действия заданным требованиям.
Подчеркнем, что действия контроля напрямую связаны с действиями
коррекции. Без коррекции контроль теряет смысл. Осознанное внесение из-
менений и пропедевтика трудностей возможны только на основе проведен-
ного контроля.
Авторитетное мнение
Д. Б. Эльконин подчеркивает, что именно действие контроля характе-
ризует всю учебную деятельность как управляемый самим ребенком про-
извольный процесс. Произвольность учебной деятельности определяется
наличием не столько намерения нечто сделать и желанием учиться, сколь-
ко (и главным образом) контролем за выполнением действия44.
Таблица 6
Операциональная характеристика регулятивных универсальных
учебных действий, связанных с контролем и коррекцией
| j № Универсальное | Операции, входящие в данное действие (осуществляется обучающимся) | |
| Контроль конечного результата собственной/чужой деятельности и его корректировка | — проверяю полученный результат: сопоставляю (сравниваю) с правильным ответом; — выявляю (вижу) допущенную ошибку (свою и/или чужую); — устанавливаю (объясняю) причину ошибки; — исправляю ошибку; — делаю вывод, как избежать такой ошибки в будущем | |
| Контроль процесса (хода) выполнения действия (своего/ чужого) и его корректировка | — различаю способ и результат выполнения («Что нужно сделать?» и «Как, каким образом это должно быть сделано?»); — формулирую способ выполнения; — «удерживаю» (помню) последовательность необходимых операций; — сопоставляю при необходимости собственное выполнение каждой операции с «шагом» алгоритма; | |
| 44 Д. Б. Эльконин. О структуре учебной деятельности//Избранные психологические тру-
|
| № п/п | Универсальное учебное действие | Операции, входящие в данное действие (осуществляется обучающимся) |
| — вношу при необходимости измен — различаю способ и результат выполнения («Что нужно сделать?» и «Как, каким образом это должно быть сделано?»); — формулирую способ выполнения; — «удерживаю» (помню) последовательность необходимых операций; — сопоставляю при необходимости собственное выполнение каждой операции с «шагом» алгоритма; — вношу при необходимости изменение в выполнение конкретной операции (в случае неправильного выполнения и пропуска «шага» алгоритма) | ||
| Проявление | — объясняю необходимость контроля как | |
| инициативы | возможности улучшения результата; | |
| выполнения | — выбираю способы контроля и определяю | |
| контроля | целесообразные для данного действия; — осуществляю контроль самостоятельно без инициирования со стороны взрослого | |
| Преодоление | — осознаю наличие конкретных учебных | |
| имеющихся | трудностей; | |
| трудностей | — устанавливаю (объясняю) причину трудностей; — ищу способы преодоления трудностей; — работаю над исправлением трудностей; — делаю вывод, как избежать трудностей в будущем |
|
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|