- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
j Универсальноеп/п учебное действие 4 страница
Обобщение важно для формулирования вывода при решении любой учеб-
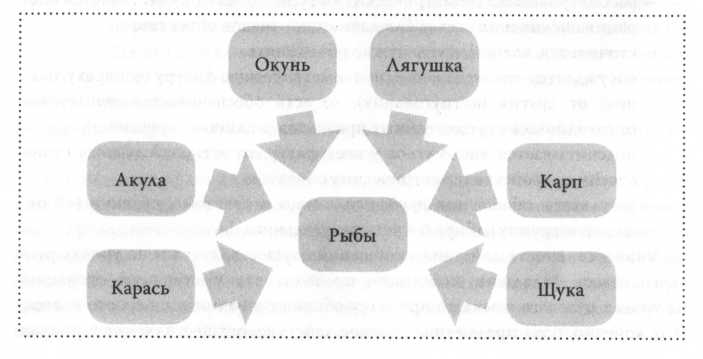
ной задачи, в том числе на уроках окружающего мира. Например, третьекласс-
никам предлагается логическая задача «Какое животное неверно отнесено
в группу рыб?».
|
|
Ученик анализирует представленное решение, мысленно проводит обоб-
щение - объединяет животных в группу «рыбы» - и делает вывод: к группе
«рыбы» не относится лягушка, она - земноводное.
Сделаем вывод: при формировании действия обобщения на универсаль-
ном уровне важнейшая задача - научить младших школьников выделять
главный, существенный признак (свойство) как необходимое основание пра-
вильного обобщения.
Обучение действию классификации
как универсальному действию
Краткая справка
Выше было сказано, что для проведения классификации ученику нужно
владеть такими мыслительными операциями, как анализ, синтез, сравнение
и обобщение. Операция анализа начинается с узнавания объекта: чтобы его
отнести к какой-то группе, его нужно назвать. Затем анализируются его свой-
ства, и среди них выделяется существенное, необходимое для проведения
классификации.
Задача учителя: каждый раз при предъявлении заданий на классифика-
цию анализировать с младшими школьниками существенный (главный)
классификационный признак. Ошибка в его выборе влечет за собой не только
неправильное выполнение конкретного задания, но и неготовность ученика
выполнять действие классификации. И в данном случае не важно, на каком
предметном содержании оно осуществляется.
Задания на классификацию могут предъявляться на разном уровне.
Самыми простыми заданиями (они возможны уже в первом классе) являются
те, где классификационный признак дается детям в готовом виде учителем.
Например, первоклассники получают задания разделить предложенные объ-
екты на две группы в соответствии со значками, которые отражают класси-
фикационный признак: О «
Результатом работы являются объединенные в группы объекты природы
(1-я группа) и изделия, созданные человеком (2-я группа). Классификационный
признак может быть представлен явно (назван) или косвенно. Приведем при-
меры заданий с неявным признаком.
1. Запиши записи с результатом 5 в один столбик, а с результатом 4 - в другой
(даны записи: 2+2, 4+1, 3+2, 3+1,1+3, 1+4, 2+3).
2. Найди омонимы, сделай в тетради таблицу и запиши примеры в каждую
графу.
| Слова, не связанные по смыслу | ||
| Одинаково звучат и пишутся | Одинаково звучат, пишутся по-разному | Одинаково пишутся, звучат по-разному |
|
|
1. Уж наступал вечер. Уж питается лягушками.
2. Зацвели душистые гвоздики. Мальчик рассыпал маленькие гвоздики.
3. Сложный код. Пушистый кот.
Задания на классификацию чаще всего предлагаются на изученном учеб-
ном содержании с целью уточнения или обобщения понятий, для формиро-
вания умения свободно пользоваться знанием. Предлагая задания на класси-
фикацию, учитель видит, какой терминологией школьники владеют (пользу-
ются активно), а какая еще не включена в активный словарь. Например, рас-
пределяя на уроке математики числовые выражения вида 100 + 45, 100 - 45,
100 + 3,100 - 3 второклассники демонстрируют знание таких весьма важных
слов и терминов: «запись», «сумма», «разность», «знак действия» и т.п.
Методический комментарий
Для успешного формирования умения классифицировать объекты ученику
нужно уметь правильно называть объекты классификационного действия.
Ученику предлагается выполнить учебную задачу на уроке математики:
распределить на две группы разные геометрические фигуры, изображенные
на рисунке. Уже сам процесс правильного проговаривания названий данных
фигур — треугольник, шестиугольник, круг, четырехугольник, круг — может
стать основой выделения классификационного признака — наличие и отсут-
ствие углов.
|
|
Первая группа —______________ •
Вторая группа —________________
В ходе классификации каждая группа «собирается» (синтезируется) посред-
ством проверки выбранного классификационного признака («У треугольника
есть углы, у шестиугольника есть, у круга нет, у четырехугольника есть, у круга
нет»). Сравнивая фигуры, отнесенные к одной группе, младший школьник вы-
деляет признак, который станет основой названия одной группы и дает назва-
ние первой группе — многоугольники. Затем педагог спрашивает: «Задание
выполнено? Как нужно поступить с остальными фигурами?» Дети подсказыва-
ют, что необходимо выделить их общий признак — это круги. На следующем
этапе решения первоклассники проводят распределение всех фигур и на этапе
проверки правильности выполнения еще раз называют каждую.


Действие классификации может помочь организовать этап закрепления
изученного. Рассмотрим пример — урок в первом классе по теме «Домашние
животные». В начале урока прошла беседа с использованием иллюстративно-
го материала, во время которой дети рассматривали и описывали различных
животных, относящихся к двум группам — домашние и дикие. Затем учитель
предлагает школьникам решить такую учебную задачу: «Распределите жи-
вотных в две группы и объясните свое решение». Для работы каждый ученик
получает рисунок.
В этой учебной ситуации выбор основания для классификации — «до-
машние-дикие» животные «спровоцирован» содержанием урока. Но часто
поиск основания для классификации является отдельной учебной задачей.
Пример задания по математике, 2-й класс. Обратим особое внимание чи-
тателей на организуемый учебный диалог как главный метод решения по-
ставленной учебной задачи.
Учебная задача: Как можно распределить числа 10, 6, 3, 60, 33,44,1,4 на груп-
пы? Найдите несколько решений.
Учитель: Как вы поняли задание? Что нужно сделать?
Дети: Распределить все эти числа на группы.
Учитель: Правильно ли я понимаю, что можно взять первые 4 числа и ска-
зать — «это первая группа, а оставшиеся 4 числа — вторая
группа»?
Нет. Нужно распределить все числа на группы по общему главно-
му признаку.
| Дети: Учитель: Дети: |
| Учитель: Петя: Лена: Гриша: Айза: Катя: Учитель: Катя: Учитель: Миша: Коля: |
групп можно распределять объекты? На две?
Можно и на две, и на три и так далее. Но нужно, чтобы основание,
признаки распределения были главными (существенными). В на-
шем случае признаки — это характеристики числа. Еще мы догово-
рились, что в каждой группе должно быть не менее двух объектов
и каждый объект можно взять и поместить в группу только один
раз.
Давайте перечислим все признаки, по которым можно распреде-
лить все числа на группы. При ответе говорите, на сколько групп
будете распределять и по какому основанию или признакам.
Я буду распределять на две группы по количеству знаков в запи-
си. В первой группе будут однозначные числа, а во
второй — двузначные.
Я буду распределять числа в две группы по их четности. В первой
группе будут четные числа, а во второй — нечетные.
А я распределю в две группы так: в одну группу круглые десятки,
а в другую некруглые десятки.
Гриша, ты не прав. Нельзя про числа 1, 3, 6, 4 сказать, что это не-
круглые десятки, потому что это не десятки. Думаю, что у тебя по-
лучатся три группы — круглые десятки, числа больше десятка
и числа меньше десятка.
Я согласна с Лизой и предлагаю Грише рассмотреть еще такой ва-
риант распределения на три группы: круглые десятки, двузначные
некруглые числа, однозначные числа.
Катя, ты сделала уточнение для второй группы — «некруглые»
числа. Почему?
Если так не сказать, то числа 10 и 60 придется писать в две группы,
а этого делать нельзя.
Какие еще способы распределения вы нашли?
Я бы еще распределил по количеству цифр в записи числа. У меня
будут 2 группы: числа, записанные с помощью одной цифры и чис-
ла, записанные с помощью двух цифр.
Миша, я не согласен. У тебя в одной группе будут числа 1,4, 3, 6, 33,
44 — и однозначные, и двузначные. Так нельзя.
Миша: Почему нельзя? Какое из правил распределения на группы я нару-
шаю? Мне нужно, чтобы все числа имели одно и то же свойство
(имеют — записаны с помощью одной цифры), я распределил все
числа (10 и 60 — вторая группа, в записи две цифры), у меня каждое
число записано в одну группу.
Учитель: Коля, Миша убедил тебя?
Коля: Да.
Познавательные универсальные учебные
действия, «участвующие» в поисковой
и исследовательской деятельности
Краткая справка
В последние годы ученые, практические работники, педагогическая обще-
ственность все чаще говорят о снижении интереса школьника к учению, о без-
различии к приобретению новых знаний, пассивности ребенка в выборе и ис-
пользовании средств познавательной деятельности. Младшие школьники
предпочитают не читать, а играть на компьютере, равнодушны к участию в на-
блюдениях, формально выполняют домашние задания. Многие учащиеся на-
чальных классов не могут назвать любимого учебного предмета, им нравится
выполнять легкие задания, они предпочитают работать по образцу, констати-
руют, что им нравится слушать то, что рассказывает учитель, но самим добы-
вать информацию неинтересно. Почему это происходит? Основной причиной,
очевидно, является не только неактуальность знаний для обучающихся,
но и малопривлекательный процесс учения: отсутствие инициативы в выборе
деятельности, преобладание репродуктивных заданий, недостаточное исполь-
зование наглядности. Учащиеся не видят ценности самостоятельного поиска
информации и не проявляют в этом отношении никаких волевых усилий.
Такая ситуация в начальном образовании ставит задачу особого внима-
ния к организации поисковой и исследовательской деятельности, которая
может внести особый вклад в познавательное и личностное развитие. Если
учитель создает условия для поиска, исследования, самостоятельного «от-
крытия» учащимся знания, факта, закономерности, то полученные таким об-
разом знания всегда будут для ребенка актуальными, личностно значимыми.
Исходя из этого, авторы данного пособия считали целесообразным вы-
делить в отдельную группу познавательных универсальных учебных дей-
ствий, «участвующий» в поисковой и исследовательской деятельности.
В нижеследующей таблице представлены три универсальных
действия — наблюдение; поиск и обнаружение нового знания на основе
опыта (исследования); моделирование отношений между объектами.
Напомним, что познавательные универсальные учебные действия как
способы решения познавательных учебных задач, характеризуются следую-
щими качествами: во-первых, они ориентированы на применения различных
методов познания, во-вторых, опираются на рациональное использование
мыслительных операций, в-третьих, требуют деятельности моделирования
и конструирования.
| № п/п | Универсальное jучебное 1 действие | Операции, входящие в данное действие (осуществляет обучающийся) |
| Наблюдение | — узнаю (выделяю) объект наблюдения; называю данные и условия проведения наблюдения; — воспроизвожу (озвучиваю) шаги предложенного плана наблюдения до его применения; — составляю самостоятельно план рассматривания объекта; — фиксирую ход и результаты наблюдения: перечисляю яркие, видимые свойства (признаков) объекта; соотношу полученные результаты с целью наблюдения; — определяю свойства, отличающие его от других объектов | |
| Поиск | — формулирую цель опыта (своими словами) как | |
| и обнаружение | его результата; | |
| нового знания | — выдвигаю предположение (отвечаю на вопросы: | |
| на основе опыта | что будет, если..? как сделать так, чтобы..?) | |
| | исследования) | и формулирую/описываю его; проверяю предположение: исследую скрытые свойства объекта; — фиксирую полученные результаты; |
| Таблица 2 |
| Операциональная характеристика познавательных |
| Nv м/и | Универсальное учебное действие | Операции, входящие в данное действие (осуществляет обучающийся) |
| — делаю вывод о правильности (ложности) предположения; — соотношу полученные результаты с поставленной целью; — формулирую выводы: описываю «новое знание» («теперь знаю, что...», «в ходе... выяснил (а), что...») | ||
| Моделирование | — выделяю отношение между объектами, | |
| отношений | указанное в задаче; | |
| между | — выбираю изученную модель для решения | |
| объектами | задачи; — соотношу полученный результат с целью |
|
|
Наблюдение как универсальное учебное действие
Краткая справка
Процесс обучения сопровождается наблюдениями за визуальными и вер-
бальными объектами. Согласно принципу природосообразности обучения
учитель начальных классов использует наглядность. Но для того, чтобы
младший школьник учился анализировать, обобщать, делать выводы, чтобы
у него формировалось умение учиться, важно, чтобы в качестве объектов на-
блюдения выступали не только наглядные образы, но и вербальные — терми-
ны, понятия, свойства, алгоритмы и т.п.
Любое наблюдение младший школьник начинает с выделения, называния
объекта — объектов окружающего мира, геометрических фигур, образов художе-
ственного произведения, групп слов и т.д. Одни наблюдения требуют незначи-
тельного времени и осуществляются непосредственно на конкретном уроке, дру-
гие требуют больше времени. Поэтому важно учить характеризовать ситуацию
наблюдения — называть данные, условия проведения. Для предупреждения сти-
хийности действий и поспешных выводов целесообразно составлять вместе
с детьми план наблюдения или предлагать делать это самостоятельно. Если уче-
ник может проговорить план наблюдения, то он может контролировать и коор-
динировать свои шаги в наблюдении («уже увидел», «осталось рассмотреть», «те-
перь записываю/фиксирую», «пропустил шаг», «нужно еще обратить внимание
на...» и т.д.). Любознательность и творчество в процессе наблюдения привет-
ствуются, ход и результаты фиксируются: ученики отмечают свойства (признаки,
характеристики) объектов. Обязательным этапом наблюдения является уста-
новление соответствия полученных результатов и цели рассматривания. Обычно
результатом наблюдения являются свойства, отличающие объект (объекты) рас-
сматривания от других, делаются выводы о его «поведении».
Методический комментарий
В результате наблюдений происходит обогащение чувственного восприя-
тия образа мира, связей, фактов, деталей. Рассмотрим примеры.
На школьном дворе висела кормушка для птиц. Учитель предложил перво-
классникам понаблюдать, какие птицы прилетают и чем они любят лакомить-
ся. Цель наблюдения — определить особенности питания зимующих птиц
и соотнести способ питания со строением клюва. Дети анализируют результа-
ты наблюдений и замечают наличие у птиц разного строения клюва: «У снеги-
ря клюв, которым легко клевать семена. Мы заметили, что ягоды рябинки сне-
гирь не ест, а только вытаскивает из них семена...». Учитель предлагает сделать
вывод: «Зависят ли особенности питания птицы от строения ее клюва?»
2. Для того чтобы ввести правило «написание слов с непроизносимым со-
гласным в корне слова» педагог организует наблюдение за языковым матери-
алом. Второклассники работают с такими словами:
1) грусть, грустить, грустный;
2) свист, свистеть, свистнуть;
3) весть, известие, известный;
3) звезда, звездочка, звездный.
Педагог предлагает им такой план наблюдения:
1. Найдем в словах корень. Установим, правильно ли мы его определили
в предложенных словах.
2. Запишем с помощью транскрипции то, как произносится последнее
слово в каждом ряду.
3. Обратим внимание, есть ли расхождение произношения корня и бук-
венной записи корня в этих словах.
4. Подчеркнем букву, которой обозначен непроизносимый согласный звук.
5. Посмотрим, между какими звуками оказывается непроизносимый
согласный.
6. Сделаем вывод о том, какие сочетания звуков в середине слова являют-
ся «опасным местом».
В данном случае организованное наблюдение не только помогает второ-
классникам подготовиться к введению достаточно сложной орфограммы,
но и показывает образец проведения наблюдения языкового явления.
При изучении математики действие наблюдения активно формируется
при работе с новыми темами. Например, «Доли». Для того чтобы ученик по-
нял и смог в дальнейшем использовать представления о доле величины, ему
предлагаются задания, позволяющие понаблюдать, как получается и выгля-
дит доля, как сравнивать доли. Например:
«Масса яблока равна 240 г. Яблоко разрезали на равные части. Для каждо-
го рисунка ответь на вопросы.
Какую часть яблока составляет одна доля?
Какова масса одной доли?
|
|
Как ты думаешь, на сколько частей нужно разделить яблоко, чтобы мас-
са доли была наименьшей?»
Для ответа на поставленные вопросы нужно, чтобы ученики:
— различали и правильно пользовались терминологией (часть, доля,
целое);
— планировали и комментировали свои действия: рассматриваю пер-
вый (второй...) рисунок, яблоко разделено на две (три...) равные ча-
сти (доли);
— находили (в соответствии с требованием задачи) массу доли.
В ходе наблюдения третьеклассники убеждаются (на визуальной осно-
ве и с помощью вычислений), что чем на большее число долей разделена
величина, тем меньше доля (ее значение в заданных единицах).
Учитель может предложить и другую модель работы над этим задани-
ем: составить коллективный план рассматривания рисунков и пошагово
его осуществлять.
Таким образом, наблюдение помогает визуализировать процесс полу-
чения младшим школьником нового знания, собирать информацию для
объяснения решения, доказательства.
Поиск и обнаружение нового знания
на основе опыта (эксперимента)
Краткая справка
Опыт — метод исследования, в процессе которого подтверждается или опро-
вергается выдвинутое предположение (гипотеза). Опыт проходит в естествен-
ных условиях, эксперимент — в специально созданных. Конечно, в строгом науч-
ном плане исследование с применением опытов и экспериментов в начальной
школе не проводится, но элементы исследовательской работы обязательно при-
сутствуют и очень важны для развития мотивированной познавательной дея-
тельности младших школьников. Эта работа всегда вызывает большую актив-
ность ребят, развивает познавательные интересы и способности. Особенно важ-
ны эти формы организации познания для формирования учебной деятельности,
т.к. любые, даже примитивные с позиции большой науки, исследовательские
действия развивают стремление к самообучению и саморазвитию.
Поисковая деятельность младшего школьника начинается с формулирова-
ния цели опыта (эксперимента). Понимание цели позволит ученику целенаправ-
ленно осуществить три важнейших исследовательских шага:
— построить предположения о ходе поиска;
— выявить информацию, ценную для получения необходимого результата;
— не отвлекаться на информацию, факты, которые не имеют отношения к ко-
нечному результату, отказываться от их учета при его получении.
Методический комментарий
Как уже было отмечено, опыт (эксперимент) начинается с осознания его цели,
то есть ответа на вопрос: «Какой результат мы должны получить?» Предпосылкой
успешной организации поиска и обнаружения (проверки, систематизации) зна-
ния является обсуждение проблемы, выдвижение предположения. Можно ска-
зать, что поисковая деятельность ученика состоялась, если:
♦ учащийся понимает, что не владеет необходимыми сведениями для реше-
ния учебной задачи, нуждается в новом знании (или его уточнении), готов
к этой деятельности;
♦ выдвигается и обсуждается предположение о возможном результате опыта
или эксперимента;
• решение учебной поисковой задачи сопровождалось анализом ее условий,
оценкой собственного знания/незнания, созданием и реализацией пошаго-
вого алгоритма выполнения;
♦ подтверждается истинность или устанавливается ложность выдвинутого
предположения.
Дальнейшее использование «открытого» в ходе опыта (эксперимента) зна-
ния, его «встраивание» в учебный опыт ребенка невозможно без фиксирования
промежуточных результатов. Оно не может быть стихийным, а продумывается
педагогом и предъявляется ученикам в виде предложения-инструкции. Важно,
чтобы обучающийся мог сформулировать самостоятельно вывод о том, нашла ли
подтверждение гипотеза, получен ли ответ на вопрос (и в чем суть этого ответа,
результата, решения).
На уроках в начальной школе педагоги предлагают своим ученикам провести
небольшие исследования, связанные с обнаружением способов выполнения за-
даний, выбором наиболее рациональных из них. При этом важно, чтобы ученики
не подменяли проблему поиска способа решения получением ответа. То есть
результатом исследования является приобретение нового знания о способах де-
ятельности: «Я умею решать, находить... такими-то способами». Например, ког-
да в третьем классе педагог знакомит детей со способами нахождения площади
прямоугольника, он может предложить провести исследование, объединившись
в пары: «Подумайте, как найти площадь этого прямоугольника разными спосо-
бами». Уточняется цель парной работы: каждая пара должна предложить вари-
ант нахождения площади данной фигуры и объяснить его целесообразность.
В данном случае третьеклассники могут обратить внимание на три способа: 1)
делить фигуру на клетки, пересчитывать количество клеток; 2) измерять длины
в сантиметрах, считать двойками, тройками, четверками, записывать действие
умножения; 3) применять умножение к вычислению площади. В результате уча-
щиеся приходят к выводу: все способы измерения площади возможны, но с уче-
том того, что мы умеем пользоваться умножением, наиболее целесообразен тре-
тий способ; очевидно, первыми двумя могут пользоваться ученики, которые
не знают, что такое умножение.
Решение исследовательских задач, выдвижение и проверка гипотез может
осуществляться с помощью проблемных вопросов, предложенных в учебнике
или сформулированных педагогом. Приведем пример.
Первоклассники читают рассказ Ю. Дмитриева «Почему на кусте выросли
грибы?». В нем говорится о том, что дети поспорили, могут ли вырасти грибы
на кустах.
«- И не может этого быть, — сказал Димка, когда соседский мальчишка начал
рассказывать про грибы, которые он видел на кустах. — Не может быть! Это, на-
верное, ягоды ты видел, а подумал, что грибы.
Соседский мальчишка обиделся.
— Что я слепой что ли? Собственными глазами видел — самые настоящие
грибы: подберезовики, белые, подосиновики.
Чтобы решить спор, пошли мы в лес».
Чтение останавливается, и учитель предлагает предположить, как закончит-
ся рассказ: «А как вы думаете, увидят ли дети на кустах грибы?»
Дети выражают готовность поверить соседскому мальчишке и говорят:
— Увидят!
— Как проверить, верно ли наше предположение? — интересуется учитель.
Чтение рассказа продолжается. Дети выясняют, что соседский мальчишка
действительно был прав: кусты были усыпаны грибами.
— А разве грибы растут на кустах?
Дети не могут ответить на этот вопрос:
— Мы не знаем, ни разу не видели, нам об этом не рассказывали...
И предлагают:
— Давайте дочитаем рассказ, наверное, об этом там сказано...
Как видно, чтение первоклассников превращается не просто в процесс фор-
мирования навыка чтения, а в целенаправленную работу по мотивированной
оценке содержания текста, построенной на анализе, сравнении информации, ос-
мысленной ее обработке. В начальной школе такое чтение — не частое явление,
потому что учитель обычно ограничивается решением частной предметной зада-
чи (в данном случае, тренировать в чтении) и недооценивает необходимости ис-
пользовать прбьедметное содержание для решения более универсальных задач,
например, развития умения работать с информацией, представленной в тексте.
Постановку проблемы (проблемного вопроса) и поиск путей ее решения мож-
но считать основным этапом исследования, отличающего его от других познава-
тельных задач. Исследование может проходить на основе непосредственной
опытной работы. К примеру, определение свойств воды (воздуха), функций орга-
нов растений и др. Очень интересно проходят и вербальные исследования, кото-
рые строятся на обсуждении выдвинутых гипотез, работе с текстами, иллюстра-
циями, справочными материалами. Разновидностью урока-исследования явля-
ется практикум. Например, в начале изучения темы «Насекомые» (3-й класс) пе-
ред детьми ставится проблема «Можно ли отнести паука к насекомым?».
Учащимися выдвигаются следующие гипотезы:
• Паука можно отнести к насекомым;
• Паука нельзя отнести к насекомым.
Ребята анализируют представленные доказательства:
1. Паука можно отнести к насекомым, потому что он похож на многих из них
(на жука, пчелу, муху), умеет ползать (как таракан, муравей), тело и лапки
состоят из члеников (как у всех насекомых).
2. Паука нельзя отнести к насекомым, потому что у него только две части тела
(а у насекомых три), нет крыльев и усиков; а также не шесть, а восемь
конечностей.
Учитель предлагает сравнить изображения насекомого и паука и установить
отличие, которое сразу бросается в глаза (используются иллюстрации или муль-
тимедиа). Ученики в качестве главного отличия выбирают число ног, что и стано-
вится определяющим для классификации этого животного: паук относится
не к насекомым, а к паукообразным, хотя общей особенностью и тех и других яв-
ляется их принадлежность к членистоногим (дополнительная информация).
Способность участвовать в исследовании, подчинять свои действия достиже-
нию цели может быть учтена учителем при выявлении детей, способных рабо-
тать самостоятельно (особенно в случаях, когда изучаемая тема носит обобщаю-
щий характер). Например, многие первоклассники умеют пользоваться линей-
кой, знают, что такое «сантиметр», могут показать его на линейке. Эти дети могут
получить задание27, целью которого является доказательство верности/неверно-
сти применения алгоритма измерения.
|
27 Математика: 1 класс: учебник для учащихся общеобразовательных учреждений: |
| % |
Первоклассник сначала читает задание 1 в учебнике, делает предположе-
ние «Оля измерила длину отрезка верно/неверно» и проверяет свое предпо-
ложение с помощью информации (алгоритм измерения длины отрезка) поме-
щенной над заданием 1. Результатом поисковой работы ученика будет ответ
«Оля измерила длину отрезка верно, Даша — неверно. Сейчас я это докажу...».
В основе доказательства — нарушение Дашей алгоритма измерения — отре-
зок приложен к линейке неправильно.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|