Варіант 11

Варіант 11

1. Виготовлено 8 деталей, з яких 2 деталі вищого ґатунку. Деталі використовуються порівно двома робітниками при збиранні механізму. Знайти імовірність того, що деталі вищого ґатунку потраплять до робітників.

2. З яких елементарних виходів складається добуток подій: поява одного герба при підкиданні двох монет; поява однієї цифри при підкиданні двох монет.

3. Виготовлено 50 деталей, з яких 20 вищого ґатунку. Знайти імовірність того, що з трьох перевіряємих деталей виявиться вищого ґатунку.

4. Існує 3 партії телефонних апаратів. Відомо, що в І і ІІІ партіях всі апарати задовольняють технічним вимогам, а у ІІ партії технічним умовам відповідають 4/5 апаратів. Знайти імовірність того, що випадково взятий апарат виявиться доброякісним.

5. На ділянці працює 6 верстатів. Імовірність зупинки верстату на якій-небудь причині дорівнює 0,01. Знайти імовірність того, що в деякий момент часу працюватимуть не менше 5 верстатів.

6. Імовірність виготовлення консервної банки з недостатньою герметизацією дорівнює 0,002. Серед скількох випадково відібраних банок можна з імовірністю 0,98 очікувати відсутність бракованих?

7. Закон розподіл дискретної випадкової величини Х задано таблицею

х	–1
р	0,3	0,25	0,2	0,1	0,15

Знайти функцію розподілу випадкової величини Х і побудувати її графік. Знайти середнє квадратичне відхилення випадкової величини Х.

8. Випадкову величину Х задано такою диференціальною функцією розподілу:

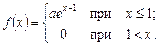
Потрібно: а) знайти коефіцієнт а; б) знайти інтегральну функцію розподіл 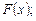в) побудувати графіки функцій 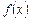і 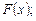г) знайти імовірність того, що дана випадкова величина набуде значення із інтервалу .

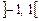9. Відомо, що в даному водоймищі 40 % коропів і 60 % інших риб. Всі риби з рівною імовірністю потрапляють на гачок. Рибалка вивуджує 5 риб. Знайти закон розподіл числа спійманих коропів. Визначити математичне сподіванняі дисперсію цієї випадкової величини.

10. Встановлено, що за великої кількості вимірювань 75 % помилок, розподілених нормально, не перевершують за абсолютною величиною 1,25 мм. Знайти відсоток помилок, не перевершують за абсолютною величиною 1 мм.

11. Закон розподіл кількості опадів, що випадають протягом року у даній місцевості, не відомий. Математичне сподіванняцієї випадкової величини дорівнює 55 см. Оцінити імовірність того, що в цій місцевості випаде більше 175 мм опадів.

12. Знайти коефіцієнт кореляції випадкових величин х і у, якщо відомий двовимірний розподіл цих величин:

х y
	0,3	0,05	—
	0,1	0,2	0,1
	0,05	—	0,2

⇐ Предыдущая 4 5 6 7 8 9 101112 13 Следующая ⇒