Рорахункова робота №№1 -2 Завдання 1-6

Стр 1 из 13Следующая ⇒

Рорахункова робота №№1 -2 Завдання 1-6

Рорахункова робота № 3 Завдання 7-9

Рорахункова робота № 4 Завдання 10-12

Ваш номер варіанту – номер за списком, якщо n від 1 до 15,

Ваш номер варіанту – номер за списком минус 15, якщо n від 16 до 30.

ВАРІАНТИ ЗАВДАНЬ ДЛЯ РОЗРАХУНКОВИХ РОБІТ

Варіант 1

1. На складі взяли 5 мішків борошна І ґатунку і 7 мішків борошна ІІ ґатунку. Довільні 6 мішків з 12 витратили на приготування одного з видів паляниць. Знайти імовірність того, що половина з цих 6 мішків борошна виявилася борошном І ґатунку.

2. Відбувається два постріли по мішені. Чи будуть несумісними дві події: відбулося хоча б одне влучення або був хоча б один промах ?

3. Імовірність того, що один з трьох ліфтів виявиться в даний момент на першому поверсі, дорівнює 0,1. Яка імовірність того, що хоча б один ліфт виявиться на першому поверсі?

4. 30% приладів збирає спеціаліст високої кваліфікації і 70% — середньої. Надійність приладу, зібраного спеціалістом високої кваліфікації, дорівнює 0,9, приладу, зібраного спеціалістом середньої кваліфікації, — 0,8. Взятий прилад працює безвідказно. Визначити ймовірності того, що він зібраний спеціалістом високої кваліфікації.

5. Імовірність того, що витрата води на деякому підприємстві виявиться нормальним, дорівнює 0,75. Знайти імовірність того, що у найближчі 6 днів витрата води буде нормальною протягом 3 днів.

6. При деякому випробуванні імовірність позитивного виходу дорівнює 0,8. Знайти імовірність того, що число позитивних виходів при 200 випробуваннях буде не менше 170.

7. Закон розподілу дискретної випадкової величини 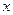заданий таблицею:

х	–7	– 6	–5	– 4	–3
р	0,2	0,25	0,1	0,15	0,3

Знайти функцію розподілу випадкової величини х і побудувати її графік. Знайти середнє квадратичне відхилення випадкової величини х.

8. Інтегральна функція розподілу випадкової величини х має вигляд

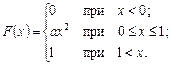
Потрібно: а) знайти коефіцієнт 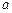; б) знайти функцію щільності розподілу 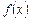; в) побудувати графіки функцій 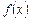і 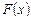; г) знайти імовірність того, що випадкова величина 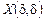набуде значення з інтервалу ]0,25; 0,5[.

9. Відомо, що випадкова величина 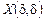може набувати значення 1, 2 і 3. Знайти імовірності цих значень, якщо математичне сподівання цієї випадкової величини дорівнює 1,8, а дисперсія дорівнює 0,56.

10. 50 % помилок приладу не виходить за межі ±10 м. Знайти процент помилок приладу, що не виходить за межі ±20 м, якщо відомо, що прилад не має систематичних помилок. Випадкові помилки підкоряються нормальному розподілу.

11. Дисперсія кожної з 2500 незалежних випадкових величин не перебільшує 5. Оцінити ймовірність того, що відхилення середнього арифметичного цих випадкових величин від середнього арифметичного їх математичного сподівання не перевищить 0,4.

12. Знайти коефіцієнт кореляції випадкових величин х і у, якщо відомий двовимірний розподіл цих величин

х у
–2	0,1	0,1	0,05	—
–1	0,05	0,2	0,2	0,05
	—	—	0,05	0,2

12 3 4 5 6 7 8 9 10 Следующая ⇒