
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Асинхронная машина.
 При записи уравнений асинхронной машины напомним об особенностях её конструкции. На статоре и на роторе машины находятся многофазные обмотки, равномерно распределенные вдоль расточки статора и ротора. Воздушный зазор между статором и ротором одинаков по любым осям, проведенным из центра вращения ротора. Это, что магнитные проводимости машины не зависят от положения ортогональных осей x, y. Другими словами, машина обладает и электрической, и магнитной симметрией. А это значит, что уравнения её электромагнитного состояния могут быть записаны в ортогональных осях x, y, вращающихся относительно статора и ротора с произвольной скоростью. При исследовании электромагнитных взаимодействий изображающие векторы многофазных величин строятся всегда в своих собственных осях, а записываются в выбранной системе ортогональных осей. Поэтому и.в. токов статора и ротора в осях x, y запишутся соответственно
При записи уравнений асинхронной машины напомним об особенностях её конструкции. На статоре и на роторе машины находятся многофазные обмотки, равномерно распределенные вдоль расточки статора и ротора. Воздушный зазор между статором и ротором одинаков по любым осям, проведенным из центра вращения ротора. Это, что магнитные проводимости машины не зависят от положения ортогональных осей x, y. Другими словами, машина обладает и электрической, и магнитной симметрией. А это значит, что уравнения её электромагнитного состояния могут быть записаны в ортогональных осях x, y, вращающихся относительно статора и ротора с произвольной скоростью. При исследовании электромагнитных взаимодействий изображающие векторы многофазных величин строятся всегда в своих собственных осях, а записываются в выбранной системе ортогональных осей. Поэтому и.в. токов статора и ротора в осях x, y запишутся соответственно
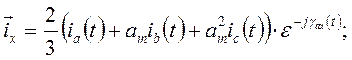 (33)
(33)
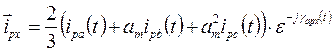 (34)
(34)
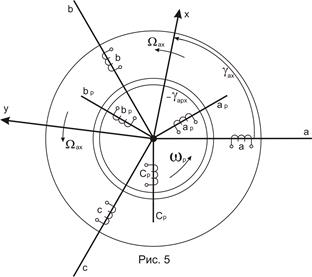
Пусть ортогональные оси x, y вращаются относительно статора со скоростью 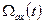 , а ротор – со скоростью ωр, рис. 5. Это значит, что оси x, y вращаются со скоростью
, а ротор – со скоростью ωр, рис. 5. Это значит, что оси x, y вращаются со скоростью 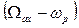 или
или  относительно ротора.
относительно ротора.
Поскольку к обмотке статора АМ в общем случае подводится многофазное напряжение, а обмотка ротора замкнута накоротко или на сопротивление, уравнения АМ в векторной форме имеют вид
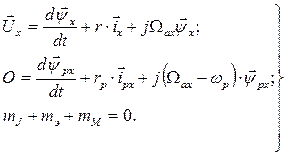 (35)
(35)
Те же уравнения в проекциях на оси x, y
 (36)
(36)
В заключение необходимо отметить, что записанные системы уравнений (32), (35), (36) для синхронной и асинхронной машины не могут быть непосредственно использованы для расчета режимов в виду того, что содержат неизвестных больше, чем уравнений. Это значит, что полученные системы уравнений необходимо дополнить уравнениями связи между переменными.
Уравнения связи.
1.  Связь между и.в. токов, и.в. намагничивающих сил и фактической (действительной) намагничивающей силой многофазной обмотки.
Связь между и.в. токов, и.в. намагничивающих сил и фактической (действительной) намагничивающей силой многофазной обмотки.
Из курса «Электрические машины» известно, что амплитуда первой (основной) гармоники пространственной волны намагничивающей силы (н.с.) фазной обмотки машины на пару полюсов как функция времени определяется выражением
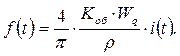 (37)
(37)
Здесь 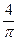 - коэффициент, связывающий амплитуду 1-й гармоники с амплитудой прямоугольной пространственной волны н.с.;
- коэффициент, связывающий амплитуду 1-й гармоники с амплитудой прямоугольной пространственной волны н.с.;
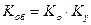 - обмоточный коэффициент, равный произведению коэффициента укорочения шага обмотки на коэффициент распределения;
- обмоточный коэффициент, равный произведению коэффициента укорочения шага обмотки на коэффициент распределения;
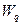 - действительное число витков в фазе обмотки;
- действительное число витков в фазе обмотки;
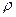 - число пар полюсов машины.
- число пар полюсов машины.
Обозначим:
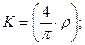
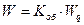 - эффективное число витков в фазе обмотки.
- эффективное число витков в фазе обмотки.
Таким образом, амплитуда пространственной волны н.с. фазной обмотки
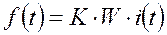 (38)
(38)
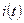 - мгновенное значение тока в фазе обмотки.
- мгновенное значение тока в фазе обмотки.
Рассмотрим 3-х фазную обмотку. Н.с. каждой фазы действует по оси соответствующей фазы и определяется током её обмотки, то-есть
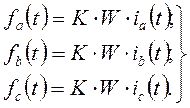 (39)
(39)
Каждую из фазных н.с. можно представить пространственным вектором, связав с ортом оси своей фазы
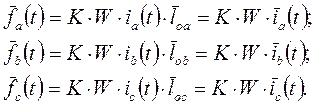 (40)
(40)
Имея пространственные векторы фазных н.с., легко записать выражение для изображающего вектора 3-х фазной системы н.с. построенных и записанных в собственных фазных осях:
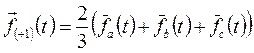 (41)
(41)
или 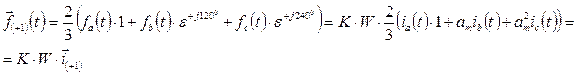
т.е. 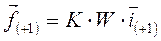 (42)
(42)
Нет необходимости доказывать, что и.в. многофазной системы н.с., записанный в ортогональных осях x, y, вращающихся с произвольной скоростью относительно фазных осей, имеет выражение

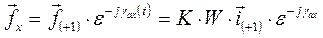 или
или
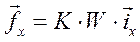 (43)
(43)
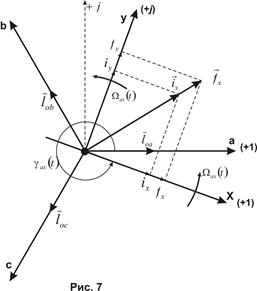 Здесь, как и ранее,
Здесь, как и ранее,  - угол между осью фазы a и осью x, смотри рис. 7. Разумеется и.в.
- угол между осью фазы a и осью x, смотри рис. 7. Разумеется и.в. 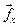 может быть разложен по осям x и y. В комплексной форме записи, считая x осью действительных, а y – мнимых, получим
может быть разложен по осям x и y. В комплексной форме записи, считая x осью действительных, а y – мнимых, получим
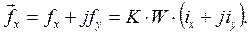 (44)
(44)
Переходя к проекциям на оси,
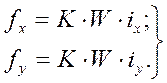 (45)
(45)
Суммарный вектор н.с. 3-х фазной обмотки.
Результирующая намагничивающая сила 3-х фазной обмотки является геометрической суммой н.с. её фазных обмоток

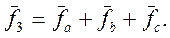 (46)
(46)
Сравнивая выражения (41) и (46), имеем:
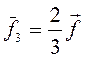 (47)
(47)
а следовательно,
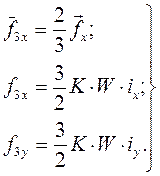 (48)
(48)
Если число фаз отличается от 3-х, m≠3 и.в. токов
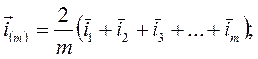 (49)
(49)
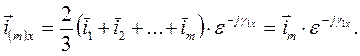 (50)
(50)
Аналогично для намагничивающих сил
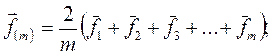 (51)
(51)
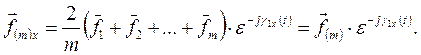 (52)
(52)
Результирующая н.с. m – фазной обмотки равна
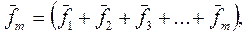 (53)
(53)
следовательно,
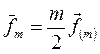 и (54)
и (54)
в осях x, y 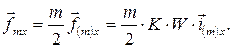 (55)
(55)
Связь между магнитными потоками, потокосцеплениями,
намагничивающими силами и токами.
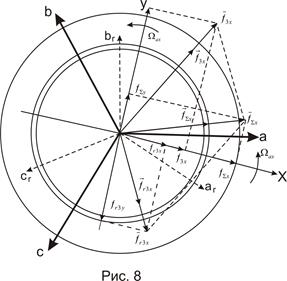 Простоты ради будем рассматривать электрическую машину, у которой на статоре и на роторе имеются 3-х фазные обмотки. Пренебрегаем краевыми эффектами и считаем поля машины плоскопараллельными. На рис. 8 представлено поперечное сечение машины, на котором показаны фазные оси, оси x, y и векторы н.с. обмоток статора и ротора. В этом случае вектор н.с. 3-х
Простоты ради будем рассматривать электрическую машину, у которой на статоре и на роторе имеются 3-х фазные обмотки. Пренебрегаем краевыми эффектами и считаем поля машины плоскопараллельными. На рис. 8 представлено поперечное сечение машины, на котором показаны фазные оси, оси x, y и векторы н.с. обмоток статора и ротора. В этом случае вектор н.с. 3-х
фазной обмотки статора в осях x, y
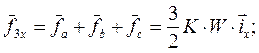 (56)
(56)
3-х фазной обмотки ротора в тех же осях
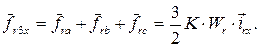 (57)
(57)
Результирующая намагничивающая сила обмоток статора и ротора машины
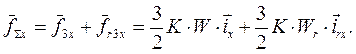 (58)
(58)
Замечание. В случае, когда на статоре и на роторе обмотки имеют различное число фаз, соответственно на статоре – m, на роторе – mr, результирующая намагничивающая сила, 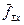 , запишется в виде выражения
, запишется в виде выражения
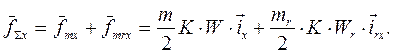 (59)
(59)
Выражение (59), в частности, можно использовать при описании асинхронного двигателя с к.з. обмоткой на роторе, у которого число фаз ротора равно числу пазов (стержней беличьей клетки) ротора.
Единый магнитный поток машины условно можно представить в виде суммы трех составляющих: потока взаимоиндукции, пронизывающего витки обмоток статора и ротора и создающего ними соответствующие потокосцепления; потока рассеяния обмотки статора и потока рассеяния роторной обмотки. Обозначим:
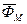 - вектор, модуль которого равен магнитному потоку взаимоиндукции, а направление совпадает с вектором наибольшей магнитной индукции этого потока (вектор потока взаимоиндукции);
- вектор, модуль которого равен магнитному потоку взаимоиндукции, а направление совпадает с вектором наибольшей магнитной индукции этого потока (вектор потока взаимоиндукции);
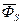 - вектор потока рассеяния обмотки статора;
- вектор потока рассеяния обмотки статора;
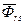 - вектор потока рассеяния обмотки ротора.
- вектор потока рассеяния обмотки ротора.
Безусловно эти векторы могут быть записаны в любых осях. При их записи в осях x, y, добавим к их обозначениям индекс x, а именно:
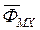 ,
, 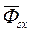 ,
, 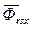 .
.
Каждый из этих потоков можно представить в виде суммы составляющих по осям x, y:
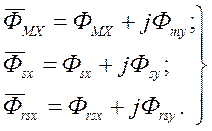 (60)
(60)
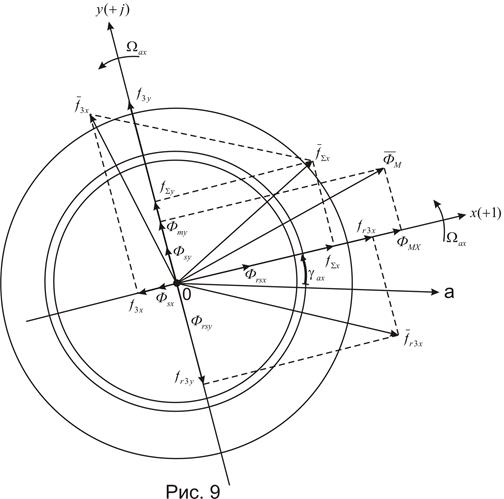
Связь между компонентами магнитных потоков по осям x и y и соответствующими компонентами намагничивающих сил определяется магнитными проводимостями машины по выбранным осям. Обозначим:
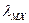 - магнитная проводимость машины потоку взаимоиндукции по оси x;
- магнитная проводимость машины потоку взаимоиндукции по оси x;
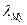 - то же, но по оси y;
- то же, но по оси y;
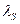 - магнитная проводимость путей рассеяния обмотки статора;
- магнитная проводимость путей рассеяния обмотки статора;
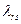 - магнитная проводимость путей рассеяния обмотки ротора.
- магнитная проводимость путей рассеяния обмотки ротора.
Так как потоки рассеяния обеих обмоток замыкаются по воздуху, проводимости им не зависят от выбора осей. Вышеизложенное позволяет записать следующие уравнения связи:
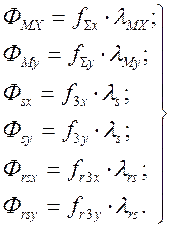 (61)
(61)
Само собой разумеется, что магнитный поток взаимоиндукции порожден результирующей (суммарной) намагничивающей силой обмоток статора и ротора, магнитный поток рассеяния статора – н.с. обмотки статора, магнитный поток рассеяния ротора – н.с. обмотки ротора.
Ввиду того что магнитные проводимости машины по осям x и y могут отличатся (а для явнополюсных машин отличаются существенно) векторы н.с. и магнитного потока, в общем случае, не совпадают. Это показано на рис. 9.
Потокосцепления, реактивности, токи.
Уравнения связи.
В принятой нами системе единиц потокосцепление ψ измеряется в вольтах, т.е. 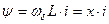 , В. Следовательно, если
, В. Следовательно, если 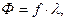
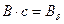 (в Веберах), т.е.
(в Веберах), т.е. 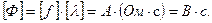 , для записи потокосцепления в принятой системе единиц необходимо магнитный поток умножить на число витков обмотки и базисную угловую частоту,
, для записи потокосцепления в принятой системе единиц необходимо магнитный поток умножить на число витков обмотки и базисную угловую частоту, 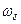 . Таким образом,
. Таким образом,
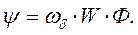 (62)
(62)
Совершенно аналогично запишется выражение для потокосцепления фазы ar ротора. С той лишь разницей, что здесь будет фигурировать число витков фазы ротора Wr, потоки рассеяния ротора по осям x и y, Фrsx и Фrsy, а также угол поворота осей x, y относительно оси фазы a ротора, ar.
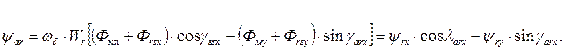 (64)
(64)
Здесь 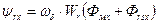 - потокосцепление фазных обмоток ротора, отнесенное к числу витков фазы, Wr , созданное составляющей магнитного потока машины, действующей по оси x, и пронизывающей фазные обмотки;
- потокосцепление фазных обмоток ротора, отнесенное к числу витков фазы, Wr , созданное составляющей магнитного потока машины, действующей по оси x, и пронизывающей фазные обмотки;
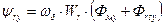 - то же, но по оси y.
- то же, но по оси y.
Из выражений для ψх, ψy, ψrx, ψry видно, что их можно рассматривать как потокосцепления с потоками взаимной индукции и рассеяния некоторых воображаемых фаз a’ и b’, a’r и b’r, которые имеют одинаковые с фазными обмотками соответственно статора и ротора эффективные числа витков, но расположены по осям x и y и вместе с последними вращаются, то-есть жестко закреплены на осях x и y, смотри рис. 11.
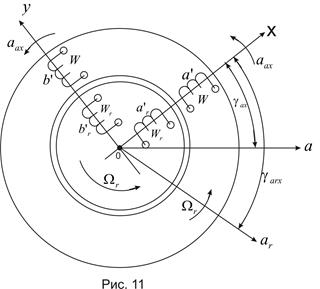 К этому же выводу можно прийти при помощи следующих простых рассуждений:
К этому же выводу можно прийти при помощи следующих простых рассуждений:
Из этого соответствия следует, что когда с осью фазы a совпадает ось x 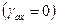 или y
или y 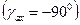
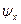 и
и 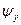 равны
равны 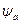 . То же относится к случаю когда оси x и y совпадают с осью фазы ar ротора. При
. То же относится к случаю когда оси x и y совпадают с осью фазы ar ротора. При 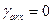 ,
, 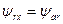 ; при
; при 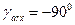 (оси y и ar совпадают)
(оси y и ar совпадают) 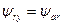 .
.
Это непосредственно вытекает из уравнений (63) и (64). Можно показать, что при совпадении осей x и y с осями фаз b и c потокосцепления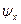 или соответственно
или соответственно 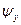 будут также равны потокосцеплениям этих фазных обмоток. Естественно предположить, что и во все остальные моменты времени
будут также равны потокосцеплениям этих фазных обмоток. Естественно предположить, что и во все остальные моменты времени 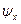 и
и 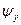 будут равны потокосцеплениям некоторых фиктивных фаз статора, расположенных по осям x и y и имеющих то же число эффективных витков, что и реальные фазные обмотки, с реальными составляющими магнитных потоков по этим осям.
будут равны потокосцеплениям некоторых фиктивных фаз статора, расположенных по осям x и y и имеющих то же число эффективных витков, что и реальные фазные обмотки, с реальными составляющими магнитных потоков по этим осям.
Все рассуждения, приведенные выше, для статорных цепей справедливы также и для цепей ротора электрической машины.
Поскольку в создании потокосцеплений фиктивных обмоток участвуют как потоки самоиндукции, при их вычислении необходимо учитывать намагничивающие силы всех обмоток статора и ротора машины.
В частности, для машины с 3-х фазными обмотками на статоре и на роотре:
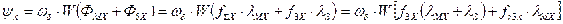 или
или
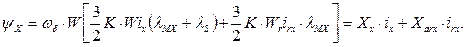 (65)
(65)
Здесь 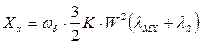 - собственная реактивность фиктивной статорной обмотки, закрепленной на оси x, приведенная к намагничивающей силе, создаваемой по оси x токами, протекающими по всем фазам статора.
- собственная реактивность фиктивной статорной обмотки, закрепленной на оси x, приведенная к намагничивающей силе, создаваемой по оси x токами, протекающими по всем фазам статора.
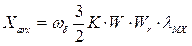 - реактивность взаимоиндукции фиктивной статорной обмотки, расположенной по оси x, приведенная к н.с., создаваемой по оси x токами, протекающими по всем 3-м фазам ротора.
- реактивность взаимоиндукции фиктивной статорной обмотки, расположенной по оси x, приведенная к н.с., создаваемой по оси x токами, протекающими по всем 3-м фазам ротора.
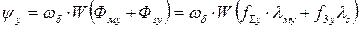 или
или
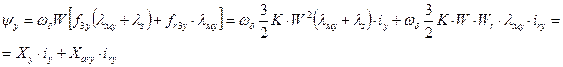 (66)
(66)
Реактивности 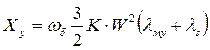
и 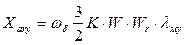 - собственная и взаимоиндукции с роторными фиктивной статорной, но закрепленной на оси y.
- собственная и взаимоиндукции с роторными фиктивной статорной, но закрепленной на оси y.
Аналогичным образом находятся потокосцепления и реактивности фиктивных роторных обмоток, закрепленных на вращающихся осях x и y:
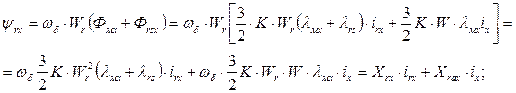 (67)
(67)
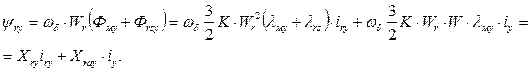 (68)
(68)
Реактивности:
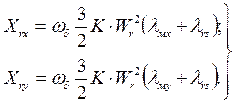 (67)
(67)
Собственные реактивности фиктивных обмоток ротора соответственно по осям x и y;
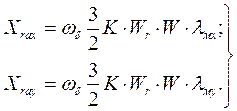 (68)
(68)
Реактивности взаимоиндукции фиктивных обмоток ротора по осям x и y со статорными цепями.
Сравнивая выражения реактивностей взаимоиндукции обмоток статора и ротора по соответствующим осям при одинаковом числе фазных обмоток на статоре и роторе, приходим к выводу: принцип взаимности соблюдается.
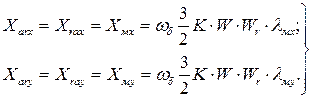 (69)
(69)
Рассмотрим наиболее общий случай машины с различным числом фаз на статоре.
Пусть m – число фаз обмотки статора;
mr – число фаз обмотки ротора.
Тогда, принимая во внимание формулы (55) и (59), можно записать для потокосцеплений  и
и 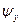 .
.
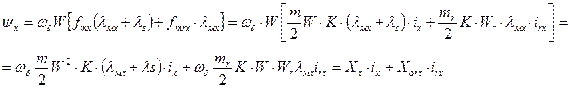 (70)
(70)
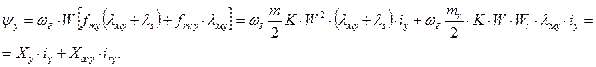 (71)
(71)
В свою очередь, для потокосцеплений 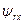 и
и 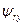 имеем:
имеем:
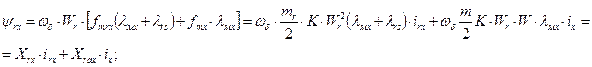 (72)
(72)
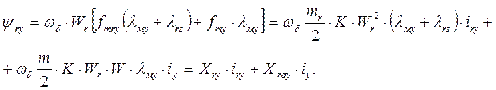 (73)
(73)
В выражениях (70 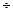 73) собственные и взаимные реактивности статорных и роторных цепей представляются формулами: для статора
73) собственные и взаимные реактивности статорных и роторных цепей представляются формулами: для статора
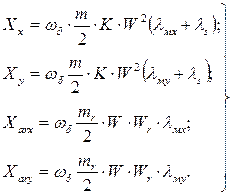 (74)
(74)
и для цепей ротора
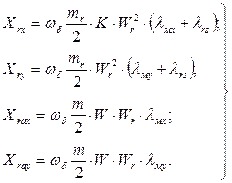 (75)
(75)
Реактивности xx, xy – называют собственными реактивностями статорной обмотки по осям x и y; xarx и xary – получили название реактивности взаимоиндукции статорной обмотки с роторной опять-таки по осям x и y. Однако упомянутые реактивности заслуживают более глубокого рассмотрения. Нам известны два вида реактивностей: самоиндукции и взаимоиндукции. Реактивность самоиндукции какой-либо обмотки в принятой системе единиц измерения характеризует отношение потокосцепления обмотки к току в этой обмотке, породившему данное потокосцепление. Реактивность взаимоиндукции предполагает наличие двух контуров с токами и характеризует отношение потокосцепления первого контура, порожденного током, протекающим по второму контуру, к току последнего и наоборот.
Реактивности, с которыми мы имеем дело, имеют несколько иной физический смысл. Действительно, обратимся, например, к выражению (70)
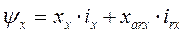 или
или
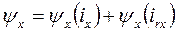 , где
, где
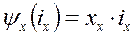 ;
; 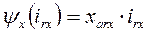 . (76)
. (76)
Здесь 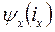 - потокосцепление фазной обмотки статора машины при совпадении оси x с осью данной обмотки, обусловленное токами, протекающими по всем m – фазам обмотки статора;
- потокосцепление фазной обмотки статора машины при совпадении оси x с осью данной обмотки, обусловленное токами, протекающими по всем m – фазам обмотки статора; 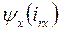 - потокосцепление фазной обмотки статора машины при совпадении оси x с осью данной обмотки, но обусловленное токами, протекающими по всем mr – фазам обмотки ротора.
- потокосцепление фазной обмотки статора машины при совпадении оси x с осью данной обмотки, но обусловленное токами, протекающими по всем mr – фазам обмотки ротора.
В соответствии с (76) собственная и взаимная реактивности определяются как
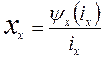
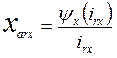 (77)
(77)
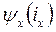 и
и 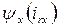 - это реальные потокосцепления фазной обмотки статора (при оговоренных условиях) или можно считать, что это потокосцепление фиктивной обмотки, закрепленной на оси x, параметры которой совпадают с параметрами фазной обмотки статора, но
- это реальные потокосцепления фазной обмотки статора (при оговоренных условиях) или можно считать, что это потокосцепление фиктивной обмотки, закрепленной на оси x, параметры которой совпадают с параметрами фазной обмотки статора, но  и
и 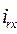 - это не реальные токи, а проекции и.в. m – фазной системы токов статора и mr – фазной системы токов ротора на ось x. Поэтому, строго говоря, xx и xarx следует рассматривать как некоторые обобщенные реактивности.
- это не реальные токи, а проекции и.в. m – фазной системы токов статора и mr – фазной системы токов ротора на ось x. Поэтому, строго говоря, xx и xarx следует рассматривать как некоторые обобщенные реактивности.
Сказанное выше относится в полной мере к реактивностям xy и xary с той лишь разницей, что в этом случае ось фазной обмотки должна совпадать с осью у принятой ортогональной системы координатных осей.
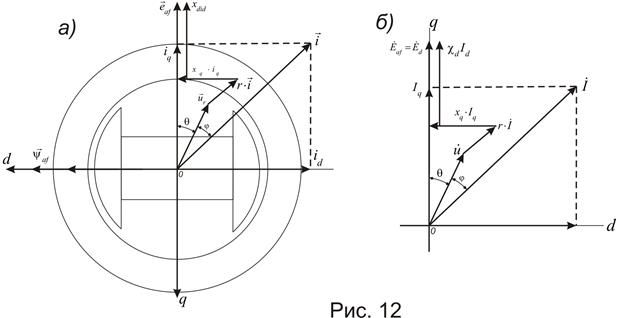
На рис. 12 показаны: а) пространственная диаграмма изображающих векторов многофазных систем параметров синхронной машины; б) векторная диаграмма комплексов, изображающих те же параметры, отнесенные к фазе обмотки, но уже переменные во времени.
Замечательным свойством изображающих векторов многофазных систем электрических и магнитных параметров электрической машины является то, что их диаграмма пространственных векторов, построенная на поперечном сечении эквивалентной 2-х полюсной машины, полностью совпадает с векторной диаграммой для временных комплексов этих же самых параметров. При этом углам сдвига по фазе соответствуют углы сдвига в пространстве машины в электрических градусах, а отношения между модулями пространственных изображающих векторов совпадают с отношениями между модулями комплексов, изображающих на векторной диаграмме переменные во времени параметры. Из этого вытекает, что реактивности собственная, xx и взаимная, xarx, которые мы нашли как некоторые обобщенные, являются одновременно соответствующими реактивностями фазной обмотки машины.
Особенности конструкции электрических машин и их влияние на выбор ортогональных осей, в которых рационально записывать уравнения.
Как известно, с точки зрения симметрии, существуют следующие типы электрических машин:
а) машины с полной электрической и магнитной симметрией относительно произвольной оси, проходящей через центр поперечного сечения; сюда относим асинхронные машины;
б) машины с магнитной симметрией и электрической асимметрией относительно произвольной оси (синхронные машины с неявновыраженными полюсами);
в) машины с электрической и магнитной асимметрией относительно произвольной оси (синхронные машины с явновыраженными полюсами и машины постоянного тока).
В асинхронных машинах, обладающих электрической и магнитной симметрией, при любом положении осей x и y магнитные проводимости для потоков взаимоиндукции и рассеяния будут оставаться неизменными по этим осям, следовательно
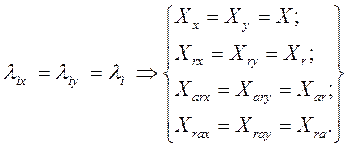 (78)
(78)
Если число фаз на статоре равно числу фаз на роторе, m=mr , то
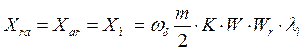 (79)
(79)
Для потокосцеплений асинхронной машины в этом случае будут справедливы следующие выражения:
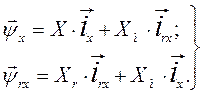 (80)
(80)
Или те же потокосцепления в проекциях на координатные оси:
 (81)
(81)
Из уравнений (74) и (75) вытекает, что для получения постоянных значений сопротивлений, а, следовательно, для получения дифференциальных уравнений электрической машины с постоянными коэффициентами, необходимо выбирать такие координатные оси, по которым магнитные проводимости машины 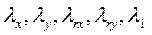 не изменяются при вращении её ротора.
не изменяются при вращении её ротора.
В явнополюсной машине, машине с электрической и магнитной асимметрией, магнитные проводимости остаются неизменными только по осям, жестко связанным с полюсами индуктора. При этом целесообразно принимать за координатные оси продольную и поперечную оси индуктора, d и q.
В этом случае проекции на оси d и q и.в. потокосцеплений обмотки якоря синхронной машины с успокоительными обмотками на полюсах индуктора будут равны:
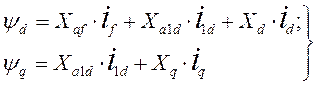 (82)
(82)
где 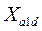 ,
, 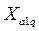 - сопротивление взаимной индукции фазы обмотки якоря с успокоительными обмотками по осям d и q при совпадении их осей;
- сопротивление взаимной индукции фазы обмотки якоря с успокоительными обмотками по осям d и q при совпадении их осей;
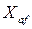 - сопротивление взаимной индукции фазы обмотки якоря с обмоткой возбуждения при совпадении их осей;
- сопротивление взаимной индукции фазы обмотки якоря с обмоткой возбуждения при совпадении их осей;
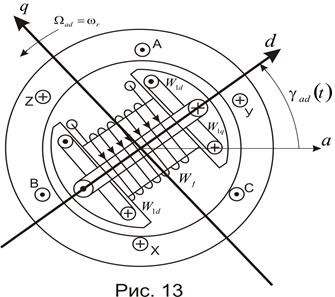 Xd и Xq – сопротивления обмотки якоря по осям d и q (имеют тот же физический смысл, что и сопротивления Xx и Xy в выражениях (74) и (77);
Xd и Xq – сопротивления обмотки якоря по осям d и q (имеют тот же физический смысл, что и сопротивления Xx и Xy в выражениях (74) и (77);
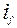 - ток в обмотке возбуждения;
- ток в обмотке возбуждения;
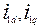 - токи в успокоительных обмотках;
- токи в успокоительных обмотках;
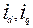 - проекции и.в. токов якоря на оси d и q.
- проекции и.в. токов якоря на оси d и q.
Потокосцепления обмотки возбуждения и успокоительных обмоток явнополюсной синхронной машины в осях d и q равны:
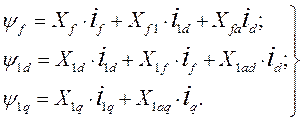 (83)
(83)
Здесь 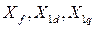 - собственные реактивности обмотки возбуждения и успокоительных;
- собственные реактивности обмотки возбуждения и успокоительных;
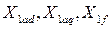 - сопротивления взаимной индукции успокоительных обмоток с обмотками якоря и возбуждения;
- сопротивления взаимной индукции успокоительных обмоток с обмотками якоря и возбуждения;
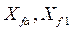 - сопротивления взаимной индукции обмотки возбуждения с многофазной обмоткой якоря и с успокоительной обмоткой по оси d.
- сопротивления взаимной индукции обмотки возбуждения с многофазной обмоткой якоря и с успокоительной обмоткой по оси d.
Выражения собственных и взаимных реактивностей явнополюсной синхронной машины.
Рассмотрим более подробно реактивности явнополюсной синхронной машины.
Пусть 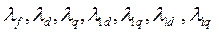 - магнитные проводимости потокам соответственно обмотки возбуждения, обмотки якоря по осям d и q, успокоительных обмоток и потокам взаимоиндукции по осям d и q;
- магнитные проводимости потокам соответственно обмотки возбуждения, обмотки якоря по осям d и q, успокоительных обмоток и потокам взаимоиндукции по осям d и q;
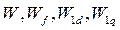 - эффективные числа витков фазы обмотки якоря, обмотки возбуждения и успокоительных обмоток по соответствующим осям.
- эффективные числа витков фазы обмотки якоря, обмотки возбуждения и успокоительных обмоток по соответствующим осям.
Тогда полные синхронные реактивности обмотки якоря по осям d и q равны:
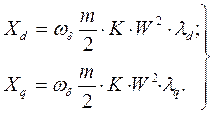 (83)
(83)
а сопротивления реакции якоря или основные реактивности обмотки якоря по осям d и q –
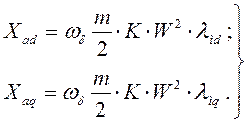 (84)
(84)
Реактивности обмотки возбуждения и успокоительных обмоток, а также реактивности взаимоиндукции находим из следующих соображений:
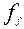 - пространственная амплитуда основной гармоники кривой н.с. обмотки возбуждения на полюсном делении
- пространственная амплитуда основной гармоники кривой н.с. обмотки возбуждения на полюсном делении
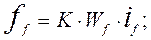
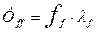 - полный магнитный поток самоиндукции обмотки возбуждения;
- полный магнитный поток самоиндукции обмотки возбуждения;
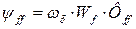 - потокосцепление самоиндукции обмотки возбуждения в синхронных вольтах;
- потокосцепление самоиндукции обмотки возбуждения в синхронных вольтах;
или 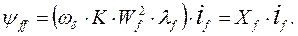
Таким образом, 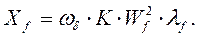 (85)
(85)
Совершенно аналогично определяются полные индуктивные сопротивления успокоительных обмоток
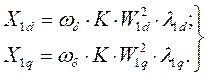 (86)
(86)
Потокосцепление фазной обмотки якоря по оси d от потока, созданного обмоткой возбуждения
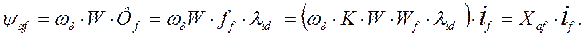
Откуда для реактивности взаимоиндукции якорной обмотки с обмоткой возбуждения имеем:
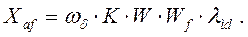 (87)
(87)
Поскольку потокосцепление 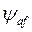 измеряется в синхронных вольтах, оно численно равно э.д.с., индуктированной в фазной обмотке статора потоки возбуждения при базисной угловой частоте,
измеряется в синхронных вольтах, оно численно равно э.д.с., индуктированной в фазной обмотке статора потоки возбуждения при базисной угловой частоте, 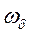 , вращения ротора
, вращения ротора
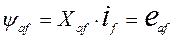 (88)
(88)
По аналогии можно записать выражения для потокосцеплений и реактивностей взаимоиндукции фазной обмотки якоря с успокоительными обмотками, а также обмотки возбуждения с успокоительной обмоткой по оси d.
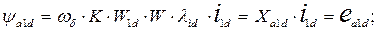 (89)
(89)
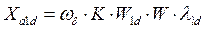 (90)
(90)
потокосцепление и реактивность взаимоиндукции фазной обмотки якоря с успокоительной обмоткой по оси d;
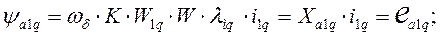 (91)
(91)
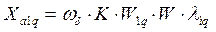 (92)
(92)
потокосцепление и реактивность взаимоиндукции фазной обмотки якоря с успокоительной обмоткой по оси q;
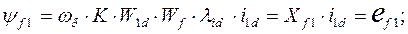 (93)
(93)
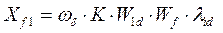 (94)
(94)
потокосцепление и реактивность взаимоиндукции обмотки возбуждения с успокоительной обмоткой по оси d;
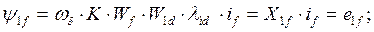 (95)
(95)
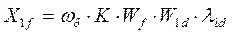 (96)
(96)
потокосцепление и реактивность взаимоиндукции успокоительной обмотки по оси d с обмоткой возбуждения.
Очевидно, не будет лишним напомнить, что обмотки, расположенные во взаимно перпендикулярных плоскостях, не взаимодействуют.
При определении потокосцеплений и реактивностей взаимоиндукций обмотки возбуждения и успокоительных обмоток с обмоткой якоряследует помнить, что эти потокосцепления создаются токами всех фаз многофазной якорной обмотки. Поэтому имеем:
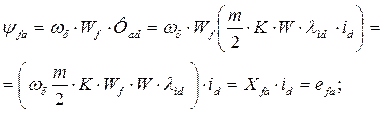 (97)
(97)
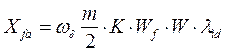 (98)
(98)
потокосцепление и реактивность взаимоиндукции обмотки возбуждения с m – фазной якорной обмоткой;
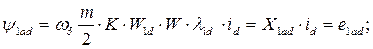 (99)
(99)
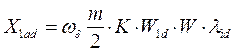 (100)
(100)
Потокосцепление и реактивность взаимоиндукции успокоительной обмотки по оси d c m – фазной якорной обмоткой;
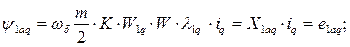 (101)
(101)
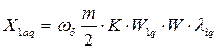 (102)
(102)
потокосцепление и реактивность взаимоиндукции успокоительной обмотки по оси q с m – фазной якорной обмоткой.
Индуктивные сопротивления обмоток статора синхронной машины в переходном и сверхпереходном режимах.
При измерении потокосцеплений обмотки в синхронных вольтах её динамическая реактивность определяется по формуле
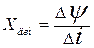 , (103)
, (103)
где 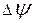 - приращение потокосцепления обмотки, соответствующее
- приращение потокосцепления обмотки, соответствующее 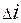 - приращению тока в ней.
- приращению тока в ней.
В синхронной машине, точнее, говоря о синхронной машине, различают два её динамических режима: переходный и сверхпереходный.
Переходным режимом синхронной машины принято считать динамический режим либо машины без успокоительных обмоток на индукторе, либо режим с момента времени, когда токи в успокоительных обмотках практически затухли. Параметры, соответствующие переходному режиму, будем обозначать теми же буквами, но со штрихом.
Синхронная машина отличается тем, что электромагнитные постоянные времени якорных обмоток значительно меньше электромагнитной постоянной времени обмотки возбуждения. Другими словами, электромагнитное поле обмотки возбуждения обладает значительно большей инерционностью по сравнению с электромагнитным полем якорной обмотки, что объясняется конструктивными особенностями машины. Результатом является тот факт, что при скачкообразном изменении режима синхронной машины (сброс или наброс нагрузки) изменение тока в якорных цепях в первоначальный отрезок времени практически не приводит к изменению потокосцепления обмотки возбуждения. То – есть обмотка возбуждения в первоначальный отрезок времени динамического режима ведет себя аналогично сверх проводящему контуру. Как известно внешним полем невозможно изменить первоначальное потокосцепление сверхпроводящего контура. Это объясняется тем, что индуктированный в сверхпроводящем контуре изменением внешнего поля ток создаст по закону электромагнитной индукции собственное приращение потокосцепления, равное внешнему, но направленное встречно. Результатом будет нулевое приращение потокосцепления. Аналогичная картина, в той или иной степени, наблюдается в индуктивно связанных контурах.
Для того, чтобы выяснить, как отражается на результирующих реактивностях якорной обмотки описанное явление, запишем уравнения для приращений потокосцеплений синхронной машины в переходном режиме, учитывая, что 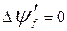 .
.
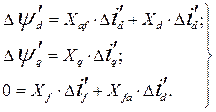 (104)
(104)
Откуда находим:
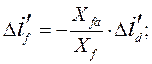
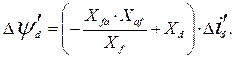
И на основании (103)
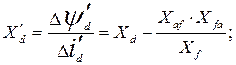 (105)
(105)
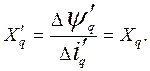 (106)
(106)
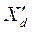 и
и 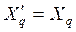 - переходные реактивности цепи якоря синхронной машины; при этом из (106) вытекает, что в переходном режиме поперечная реактивность;
- переходные реактивности цепи якоря синхронной машины; при этом из (106) вытекает, что в переходном режиме поперечная реактивность; 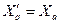 , равна своему значению в установившемся режиме, это объясняется тем, что по поперечной оси индуктора якорная обмотка не взаимодействует с обмоткой возбуждения.
, равна своему значению в установившемся режиме, это объясняется тем, что по поперечной оси индуктора якорная обмотка не взаимодействует с обмоткой возбуждения.
Чтобы оценить величину 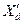 раскроем выражения реактивностей, входящих в формулу (105) для
раскроем выражения реактивностей, входящих в формулу (105) для 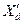 .
.
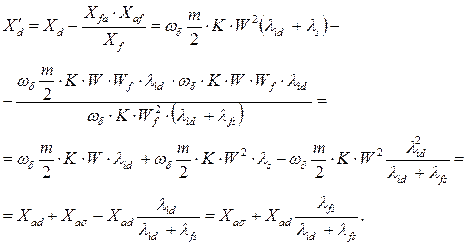 (107)
(107)
Ввиду того, что проводимость потокам рассеяния обмотки возбуждения, 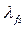 , много меньше проводимости потоку взаимоиндукции машины по продольной оси,
, много меньше проводимости потоку взаимоиндукции машины по продольной оси, 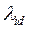 .
.
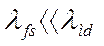 ,
,
переходная реактивность