
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Асинхронная машина. 9 страница
Это позволяет построить вектор 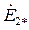 в виде (рис. 37)
в виде (рис. 37)

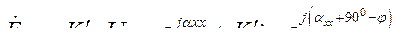
Умножив все компоненты вектора 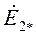 на
на 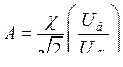 , получим некоторый условный вектор
, получим некоторый условный вектор 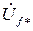 , модуль которого равен напряжению на обмотке возбуждения в о.е.,
, модуль которого равен напряжению на обмотке возбуждения в о.е., 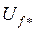 . Следовательно, можно записать
. Следовательно, можно записать

Последнее выражение позволяет достаточно просто найти вариацию 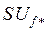 через вариации
через вариации 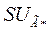 и
и  . Действительно
. Действительно
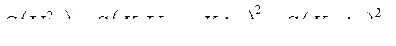
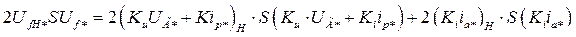
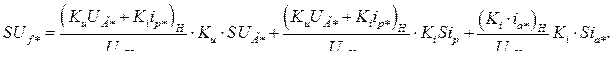
Здесь и далее 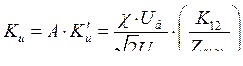 и
и 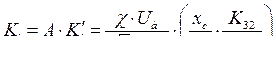 - коэффициенты усиления системы фазового компаундирования соответственно по напряжению генератора и по току его нагрузки.
- коэффициенты усиления системы фазового компаундирования соответственно по напряжению генератора и по току его нагрузки.
Из рис. 37 следует, что  и
и 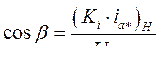 .
.
В режиме автономной работы СГ на заданную нагрузку ни угол 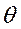 , ни
, ни 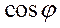 практически не зависят от колебаний скорости вращения. Поэтому можно принять
практически не зависят от колебаний скорости вращения. Поэтому можно принять
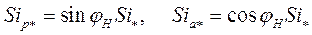 .
.
Это позволяет записать выражение 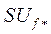 в виде
в виде
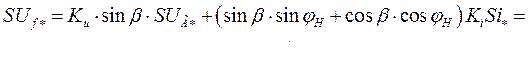 (301)
(301)
Если рассматривать 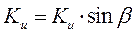 и
и 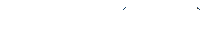 как некоторые результирующие коэффициенты усиления, то приходим к выводу, что в системе ФК коэффициенты усиления по напряжению и по току зависят от величины и характера нагрузки.
как некоторые результирующие коэффициенты усиления, то приходим к выводу, что в системе ФК коэффициенты усиления по напряжению и по току зависят от величины и характера нагрузки.
2. Уравнения СГ как объекта регулирования напряжения.
Уравнение электрического равновесия при работе на нагрузку 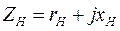 можно в о.е. записать в виде (индекс * опускаем)
можно в о.е. записать в виде (индекс * опускаем)
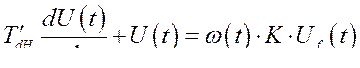 (302)
(302)
Здесь 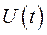 напряжение в о.е. на выходе генератора;
напряжение в о.е. на выходе генератора; 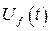 - напряжение в о.е. на обмотке возбуждения;
- напряжение в о.е. на обмотке возбуждения; 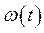 - угловая частота вращения ротора в о.е. Все переменные – функции времени. При выводе уравнения (302) использованы известные соотношения
- угловая частота вращения ротора в о.е. Все переменные – функции времени. При выводе уравнения (302) использованы известные соотношения 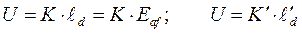 , где
, где
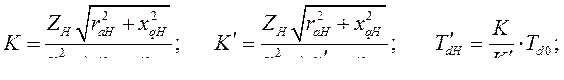
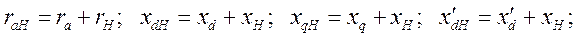
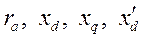 - сопротивления СГ;
- сопротивления СГ; 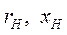 - активное и реактивное сопротивления нагрузки. Примечание. Все сопротивления берутся либо в Омах, либо в о.е., где
- активное и реактивное сопротивления нагрузки. Примечание. Все сопротивления берутся либо в Омах, либо в о.е., где 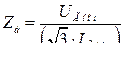 , Ом.
, Ом.
Время, а следовательно, и 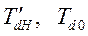 берутся в радианах.
берутся в радианах.
Перепишем уравнение (301) в операторной форме и в вариациях и разрешим его относительно вариации 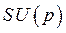 .
.
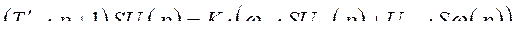 (303)
(303)
Или
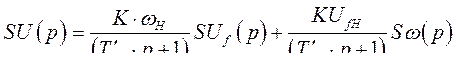 .
.
3. Уравнение динамического равновесия
В соответствии с принципом Даламбера, алгебраическая сумма моментов, включая динамический, в любом режиме генераторного агрегата равна нулю 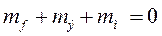 .
.
Это же уравнение в о.е. с учетом знаков моментов и известного факта, что в о.е. 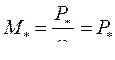 , т.е. моменты в о.е. равны мощностям в о.е., приводится к виду
, т.е. моменты в о.е. равны мощностям в о.е., приводится к виду
 (304)
(304)
Здесь 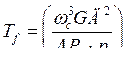 рад
рад 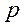 - оператор дифференциалов по синхронному времени, мощности в о.е.
- оператор дифференциалов по синхронному времени, мощности в о.е.
Запишем уравнение (304) в операторной форме и в вариациях принимая во внимание следующее: 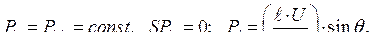
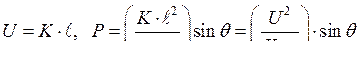
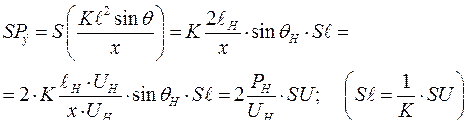
Таким образом, имеем:
 (305)
(305)
Замечание. При автономной работе СГ на нагрузку угол 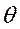 между векторами
между векторами 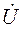 и
и  определяется исключительно величиной и характером нагрузки и практически не зависит ни от
определяется исключительно величиной и характером нагрузки и практически не зависит ни от 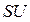 ни от
ни от 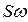 .
.
4. Общая система уравнений. Критерий устойчивости
Состоит из уравнений (301), (303) и (305). Запишем её в матричной форме, учитывая, что 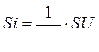 .
.
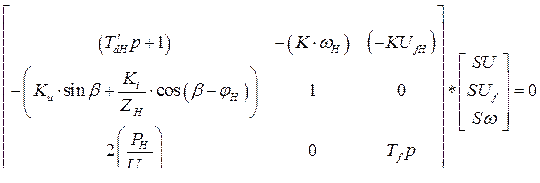 (306)
(306)
Определитель матрицы коэффициентов приравненный нулю является характеристическим уравнением системы
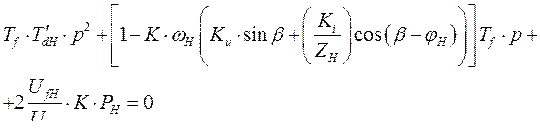 (307)
(307)
Или 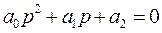
При 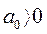 и
и 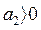 . Для того, чтобы корни характеристического уравнения имели отрицательные действительные части, необходимо, чтобы
. Для того, чтобы корни характеристического уравнения имели отрицательные действительные части, необходимо, чтобы 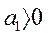 . Таким образом, критерием устойчивости работы СГ на нагрузку с системой АРВ на основе фазового компаундирования без корректора напряжения будет условие
. Таким образом, критерием устойчивости работы СГ на нагрузку с системой АРВ на основе фазового компаундирования без корректора напряжения будет условие
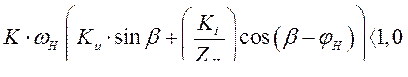 (308)
(308)
В АРВ существующих СГ система фазового компаундирования обязательно дополняется корректором напряжения с целью повышения точности регулирования и повышения устойчивости. В этом случае закон регулирования напряжения на обмотке возбуждения СГ можно записать в виде
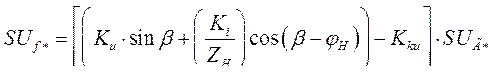 (309)
(309)
а критерий устойчивости –
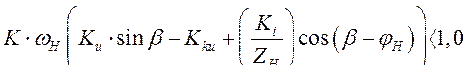 (310)
(310)
5. Определение расчетных параметров
Сделаем это на примере синхронного генератора МСК 1250-1500. Его параметры:  =1250кВа,
=1250кВа, 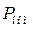 =1000кВт,
=1000кВт, 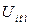 =400В,
=400В, 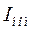 =1810А,
=1810А, 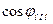 =0,8,
=0,8, 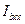 =82А,
=82А, 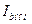 =214А,
=214А, 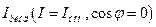 =250А,
=250А,
Обмотка возбуждения:  =0,182Ом,
=0,182Ом, 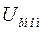 =38В,
=38В, 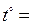 1200,
1200, 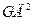 =300кг∙м2,
=300кг∙м2,
Якорная обмотка
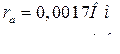 ,
,  =2,053 о.е.,
=2,053 о.е., 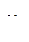 =1,0 о.е.,
=1,0 о.е., 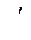 =0,213 о.е.
=0,213 о.е.
 =0,1276 Ом,
=0,1276 Ом,  =0,15 о.е.,
=0,15 о.е., 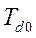 =3,5 сек. Данные в результате расчета АРВ генератора:
=3,5 сек. Данные в результате расчета АРВ генератора: 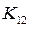 =9,0;
=9,0; 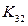 =0,075;
=0,075; 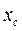 =30,05 Ом;
=30,05 Ом; 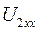 =6,385В.
=6,385В.
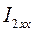 =67А;
=67А; 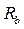 =0,0953 Ом;
=0,0953 Ом; 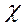 =2,34 о.е.
=2,34 о.е.
Рассмотрим номинальный режим. Расчет производим в о.е. В этом случае 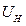 =1,0 о.е.,
=1,0 о.е., 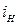 =1,0 о.е.,
=1,0 о.е., 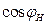 =0,8,
=0,8, 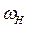 =1,0 о.е.,
=1,0 о.е., 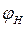 =36,870.
=36,870.
В таблице 2 приведены расчетные параметры в зависимости от 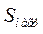 в о.е.
в о.е.
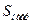
| 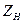
| 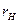
| 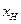
| 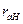
| 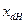
| 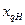
| 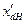
| 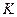
| 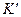
| 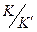
|
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 1,0 | 1,0 | 1,0 | |
| 0,25 | 4,0 | 3,2 | 2,4 | 3,213 | 4,453 | 3,4 | 2,613 | 0,7348 | 0,9742 | 0,7542 |
| 0,5 | 2,0 | 1,6 | 1,2 | 1,613 | 3,253 | 2,2 | 1,413 | 0,5591 | 0,9554 | 0,5852 |
| 0,75 | 1,333 | 1,0666 | 0,8 | 1,08 | 2,853 | 1,8 | 1,013 | 0,4440 | 0,9359 | 0,4744 |
| 1,0 | 1,0 | 0,8 | 0,6 | 0,813 | 2,653 | 1,6 | 0,813 | 0,3658 | 0,9148 | 0,3998 |
| 1,25 | 0,8 | 0,64 | 0,48 | 0,653 | 2,533 | 1,48 | 0,693 | 0,3099 | 0,8912 | 0,3477 |


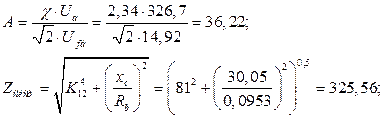
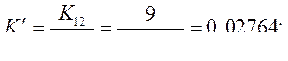
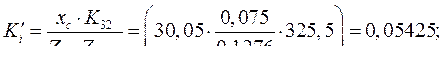
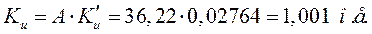
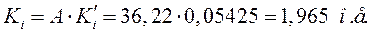
Из треугольника на рис. 37 для исследуемого (номинального) режима находим угол 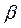 , при этом
, при этом 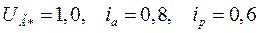 . Таким образом
. Таким образом 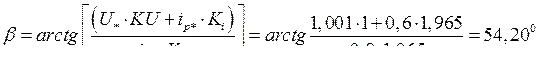
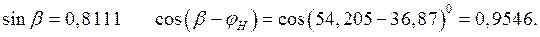
из таблицы 2 для  =1 находим
=1 находим 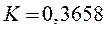 . Критерий устойчивости
. Критерий устойчивости
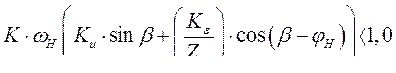
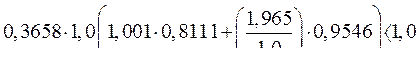
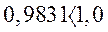
СГ с АРВ без корректора напряжения в номинальном режиме близок к границе устойчивости, поэтому введение дополнительных обратных связей не только увеличивают точность, но и способствуют увеличению запаса устойчивости.
Синхронная машина в асинхронном режиме.
 Асинхронный режим синхронной машины это работа с мощной сетью при постоянном скольжении. В этом режиме нас, прежде всего, интересует величина асинхронного момента синхронной машины. При его определении рассматриваем асинхронный режим машины без успокоительных обмоток. В асинхронном режиме результирующая э.д.с. машины имеет составляющую, определяемую напряжением на обмотке возбуждения и составляющую, определяемую скольжением ротора. Именно эта последняя и определяет асинхронный момент.
Асинхронный режим синхронной машины это работа с мощной сетью при постоянном скольжении. В этом режиме нас, прежде всего, интересует величина асинхронного момента синхронной машины. При его определении рассматриваем асинхронный режим машины без успокоительных обмоток. В асинхронном режиме результирующая э.д.с. машины имеет составляющую, определяемую напряжением на обмотке возбуждения и составляющую, определяемую скольжением ротора. Именно эта последняя и определяет асинхронный момент.
Электромагнитная мощность, а через неё электромагнитный момент, находится из выражения
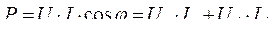 (311)
(311)
Для неявнополюсной машины при неучете активного сопротивления якоря это выражение приводится к виду
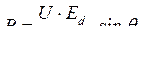 (312)
(312)
При постоянном скольжении 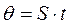 .
.
В динамическом режиме э.д.с. генератора определяется уравнением
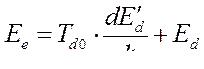 (313)
(313)
Здесь 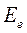 - э.д.с. в установившемся синхронном режиме при заданном неизменном напряжении источника, питающего обмотку возбуждения
- э.д.с. в установившемся синхронном режиме при заданном неизменном напряжении источника, питающего обмотку возбуждения
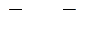
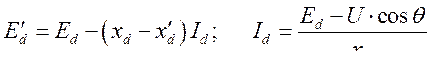 (314)
(314)
Используя (313), находим
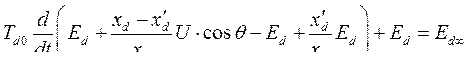
Или
 (315)
(315)
Функциями времени являются 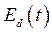 и
и 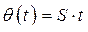 ,
, 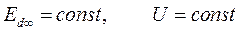
Обозначим
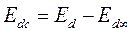 , следовательно
, следовательно
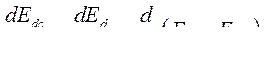
Это позволяет уравнение (315) переписать в виде
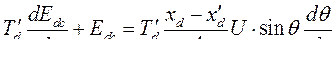
При постоянном скольжении 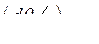 , таким образом,
, таким образом,
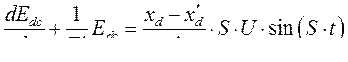
 - составляющая э.д.с. синхронной машины, порожденная скольжением ротора. Её величину находим, пользуясь операторным методом решения дифференциальных уравнений
- составляющая э.д.с. синхронной машины, порожденная скольжением ротора. Её величину находим, пользуясь операторным методом решения дифференциальных уравнений
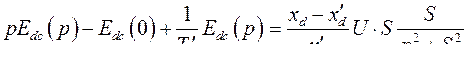
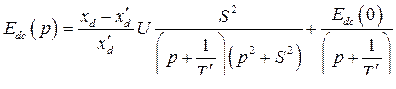 (316)
(316)
Используя обратное преобразование Лапласа, находим
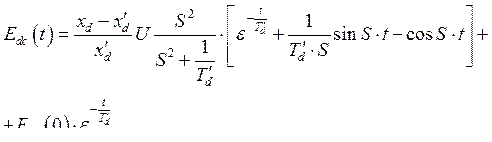 (317)
(317)
В виду того, что нас интересует квазиустановившейся режим работы синхронной машины с постоянным скольжением, в уравнении (317) отбрасываем затухающие экспотенциально составляющие.
Э.д.с. установившегося асинхронного режима, возникающая в обмотке статора исключительно за счет скольжения ротора, будет равна
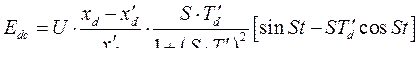 (318)
(318)
Эту э.д.с породило магнитное поле, являющееся результатом суммирования поля реакции якоря, вращающегося относительно статора с синхронной скоростью и поля ротора, вращающегося относительно статора со скоростью  . В результате э.д.с изменяется с частотой
. В результате э.д.с изменяется с частотой  (что видно из формулы). Подставив найденную э.д.с. в выражение электромагнитной мощности, (311), получим
(что видно из формулы). Подставив найденную э.д.с. в выражение электромагнитной мощности, (311), получим
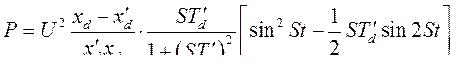 (319)
(319)
Среднее значение этой мощности за один оборот ротора. Помним, что 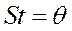 .
.
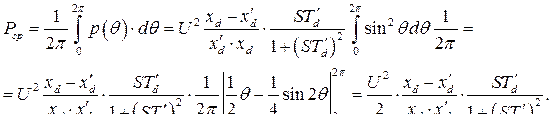 (320)
(320)
Электромагнитный момент асинхронного режима, отнесенный к асинхронной угловой частоте будет
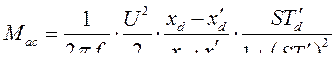 (321)
(321)
Регулирование генераторных агрегатов.
Генераторный агрегат является основным элементом электромеханической системы генерирования тока. Генераторные агрегаты могут работать автономно или параллельно с другими генераторами. В любом случае возникает задача поддержания на заданном уровне напряжения и частоты вращения, а также задача распределения между агрегатами активных и реактивных мощностей. Функции регулирования параметров в электромеханических системах решают соответствующие регуляторы. Каждый генераторный агрегат имеет, по меньшей мере, два регулятора: регулятор возбуждения и регулятор частоты. Эти регуляторы осуществляют также функции распределения активных и реактивных мощностей при параллельной работе, рис. 39.

В регуляторах сочетаются весьма разнообразные по конструкции и исполнению механические, гидравлические, пневматические, электрические, электронные и прочие устройства, составляя, в общем, сложный комплекс взаимодействующих звеньев. К регуляторам предъявляют серьезные и часто противоречивые требования, а именно: высокая точность поддержания заданных параметров в статических и динамических режимах в сочетании с высоким быстродействием при одновременном обеспечении как статической, так и динамической устойчивости.
Разработка и анализ систем автоматического регулирования является предметом теории систем автоматического регулирования.
Задача настоящей главы – напомнить основополагающие принципы теории автоматического управления применительно к разработке регуляторов возбуждения и частоты генераторных агрегатов, отвечающих требованиям заданной точности при обеспечении устойчивости работы электроэнергетической системы.
Законы регулирования.
Рассмотрим законы регулирования применительно к типовой схеме системы автоматического регулирования, изображенной на рис. 40. здесь
 ЧЭ – чувствительный элемент;
ЧЭ – чувствительный элемент;
РО – регулируемый объект;
ПУ – преобразующее, промежуточное устройство;
ИЭ – исполнительный элемент.
При отсоединении РО от чувствительного элемента имеем «разомкнутую» систему автоматического регулирования, её передаточная функция – уравнение (325). При подаче регулируемой величины с противоположным знаком, 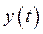 , с выхода регулируемого объекта, РО, на вход чувствительного элемента, ЧЭ, мы как бы замыкаем систему автоматического регулирования и она называется «замкнутой» (в отличие от «разомкнутой»).
, с выхода регулируемого объекта, РО, на вход чувствительного элемента, ЧЭ, мы как бы замыкаем систему автоматического регулирования и она называется «замкнутой» (в отличие от «разомкнутой»).
Напомним уравнения, связывающие параметры типовой системы автоматического регулирования (САР). Начнем с «разомкнутой» САР.
Управляющее воздействие, которое прикладывается к РО,
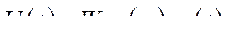 (322)
(322)
где 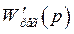 - передаточная функция цепи регулирования.
- передаточная функция цепи регулирования.
Регулируемая величина, 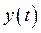 :
:
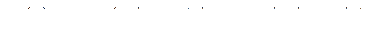 (323)
(323)
Здесь  и
и 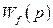 - соответственно передаточные функции объекта регулирования по регулирующему воздействию,
- соответственно передаточные функции объекта регулирования по регулирующему воздействию, 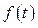 .
.
Подстановка (322) в (323) даёт:
 (324)
(324)
В этом уравнении,
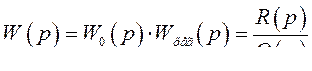 (325)
(325)
называют передаточной функцией разомкнутой системы.
При нулевых начальных условиях и возмущающих воздействиях изображения входа и выхода разомкнутой САР связаны уравнением
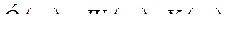 , откуда
, откуда
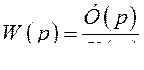 (326)
(326)
То – есть передаточная функция разомкнутой системы определяется как отношение изображения регулируемой величины и ошибки, 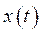 . Здесь
. Здесь 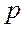 уже не оператор дифференцирования, а некоторая переменная комплексная величина,
уже не оператор дифференцирования, а некоторая переменная комплексная величина, 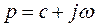 , позволяющая связать функцию времени,
, позволяющая связать функцию времени, 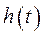 , с её изображением
, с её изображением 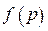 при помощи интегрального преобразования Лапласа
при помощи интегрального преобразования Лапласа
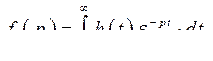
Применительно к функциям времени, которые использовались в уравнениях (322) ÷ (324), передаточная функция разомкнутой системы позволяет записать в символической или операторной форме дифференциальное уравнение, связывающее регулируемую величины 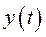 с ошибкой
с ошибкой 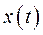
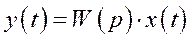 (327)
(327)
но здесь 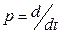 - символ дифференцирования.
- символ дифференцирования.
Рассмотрим замкнутую САР. При этом так называемое уравнение замыкания имеет вид
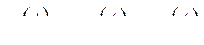 (328)
(328)
Совместное решение уравнений (324) и (328) дает для регулируемой величины выражение
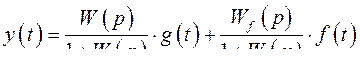 (329) и для ошибки
(329) и для ошибки
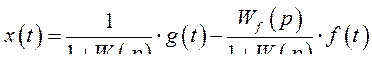 (330) выражение
(330) выражение
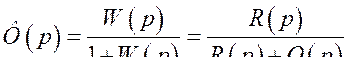 (331) является передаточной функцией замкнутой системы. Его называют также главным оператором. При отсутствии возмущающих воздействий,
(331) является передаточной функцией замкнутой системы. Его называют также главным оператором. При отсутствии возмущающих воздействий, 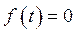 ,
,
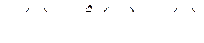 (332)
(332)
а ошибка
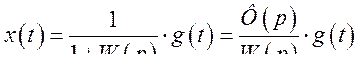
Последнее выражение может быть преобразовано и приведено к более простому виду, действительно:
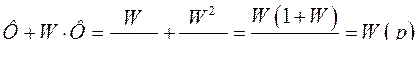
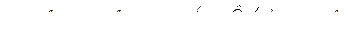 , следовательно
, следовательно
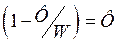 откуда
откуда 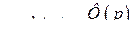 , таким образом
, таким образом
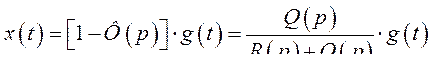 (333)
(333)
Выражение  (334) называют передаточной функцией замкнутой системы по ошибки.
(334) называют передаточной функцией замкнутой системы по ошибки.
Передаточная функция разомкнутой САР может быть найдена по передаточной функции замкнутой САР, 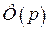 , или по передаточной функции ошибки,
, или по передаточной функции ошибки, 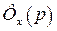 , с помощью выражений
, с помощью выражений
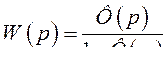 (335)
(335)
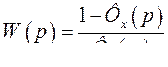 (336)
(336)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|