- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Асинхронная машина. 8 страница
Относительно легко показать, что для явнополюсной синхронной машины критерий статической устойчивости по»сползанию ротора» остается тем же (259). Покажем это без подробных пояснений, т.к. они, учитывая предыдущий материал, тривиальны. Одно лишь замечание. В случае явнополюсной СМ явление явнополюсности влияет на величину электромагнитной мощности куда более существенно, чем активное сопротивление цепи якоря. Поэтому исходную систему уравнений запишем в виде
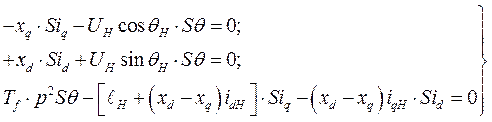 (260)
(260)
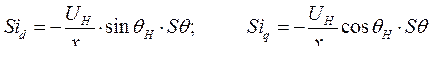
Уравнения установившегося режима.
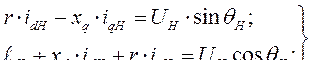
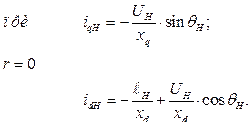
Электромагнитная мощность при 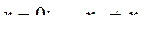

Производная от электромагнитной мощности по углу 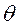
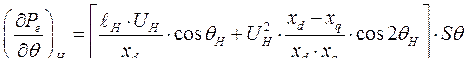 (261)
(261)
Найдем вариацию электромагнитной мощности в исходной системе уравнений (260)
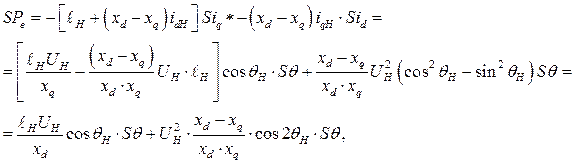
то – есть 
и уравнение механического равновесия приводится к виду
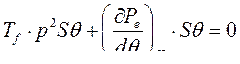
Как показано выше, решение данного уравнения дает критерий устойчивости системы в виде
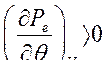
Статическая устойчивость синхронной машины при
параллельной работе с мощной сетью и при учете
переходных колебаний в цепи обмотки возбуждения.
При рассмотрении данного вопроса уравнения электрического и механического состояния машины запишем, опираясь на векторную пространственную диаграмму синхронной машины, изображенную на рис. 33.
 В соответствии с принятым положительным направлением осей имеем
В соответствии с принятым положительным направлением осей имеем
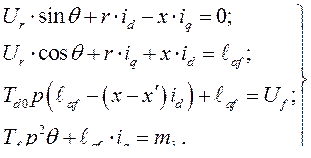 (262)
(262)
Первые два уравнения системы (262) позволяют найти составляющие тока в исходном установившемся режиме, а именно
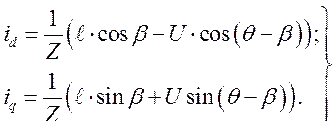 (263)
(263)
В виду того, что при работе СМ с сетью её напряжение по модулю равно напряжению сети и мы оперируем единственной э.д.с., в системе (263) и даже в этом параграфе индексы при напряжении и э.д.с. опускаем.
Запишем уравнения 3 и 4 системы (262) в вариациях. Как и в случае исследования устойчивости по «сползанию ротора», считаем
 но
но
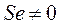 .
.
Таким образом,
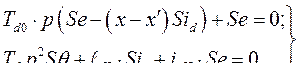 (264)
(264)
Вариации 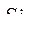 и
и 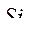 находим из уравнений (264)
находим из уравнений (264)
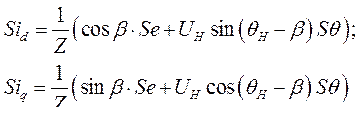
Подставив найденные выражения для  и
и  в уравнения системы (264), получим:
в уравнения системы (264), получим:
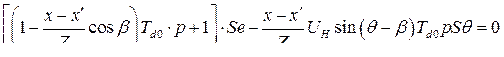 и
и
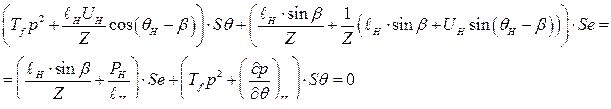
Запишем найденные дифференциальные уравнения в виде системы в матричной форме
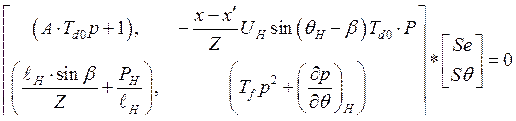 (265)
(265)
Здесь
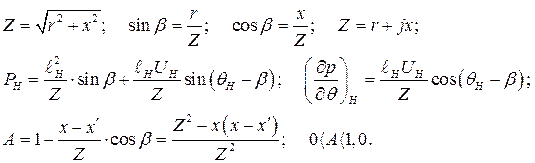
Характеристическим уравнением системы однородных дифференциальных уравнений (265) является определитель матрицы сомножителя матрицы переменных приравненный нулю, т.е.
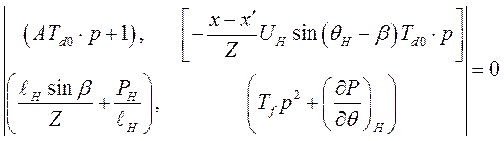 (266)
(266)
Раскрыв определитель (266), имеем
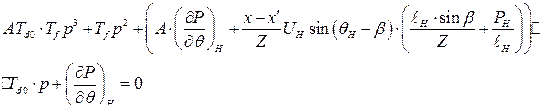 (267)
(267)
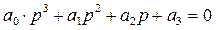
где
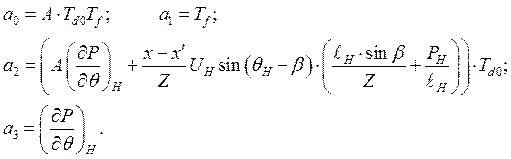
 Ввиду того, что дифференциальное уравнение имеет третий порядок, анализ устойчивости системы удобнее всего произвести с помощью критерия Гурвица. Определитель Гурвица для системы 3-го порядка имеет вид.
Ввиду того, что дифференциальное уравнение имеет третий порядок, анализ устойчивости системы удобнее всего произвести с помощью критерия Гурвица. Определитель Гурвица для системы 3-го порядка имеет вид.
Система будет устойчивой, если все диагональные определители будут положительны, то – есть:
 и
и  при
при 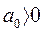
Имеем: 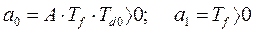 . Остаются условия
. Остаются условия
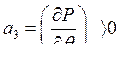 - условие устойчивости по «сползанию ротора», должно выполнятся, а также условие
- условие устойчивости по «сползанию ротора», должно выполнятся, а также условие
 (268)
(268)
При 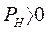 - генераторный режим, условие (268) выполняется при
- генераторный режим, условие (268) выполняется при
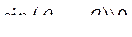
Таким образом, при параллельной работе с мощной сетью синхронного генератора и неучете регулирования возбуждения и частоты критериями устойчивости являются требования:
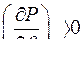 и
и 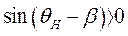 или
или 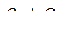 . (269)
. (269)
Для суждения о характере нарушения устойчивости при нарушении критерия (269), рассмотрим поведение системы на границе устойчивости. Эта граница определяется условием
 (270)
(270)
Рассмотрим характеристическое уравнение третьей степени
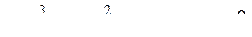 (271)
(271)
Пусть все коэффициенты – положительные величины:
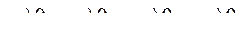
В рассматриваемом случае это условие выполняется при  .
.
В уравнениях с вещественными коэффициентами комплексные корни являются попарно сопряженными, откуда следует, что в уравнениях нечетной степени будет хотя бы один вещественный корень. Далее, так как все коэффициенты приняты положительными, то вещественный корень не может быть положительным, так как никакое положительное число не может обратить уравнение (271) в нуль, если его коэффициенты – положительные числа. Ясно, что в данном случае неустойчивость может быть только за счет положительности вещественной части комплексных корней.
Граница устойчивости получается, когда вещественная часть пары комплексных корней равна нулю.
Это будет иметь место, если при 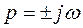 уравнение (271) удовлетворяется. Найдем соотношения между коэффициентами, при которых комплексные корни лежат на мнимой оси (граница устойчивости). Подставим в (271)
уравнение (271) удовлетворяется. Найдем соотношения между коэффициентами, при которых комплексные корни лежат на мнимой оси (граница устойчивости). Подставим в (271) 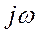 вместо
вместо 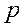 . Получим
. Получим
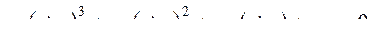 (272)
(272)
Отделяя вещественные члены от мнимых, найдем
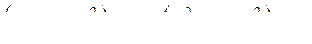 (273)
(273)
Уравнение (273) будет удовлетворено, когда его действительная (вещественная) и мнимая части, каждая в отдельности, будут равны нулю при одном и том же значении 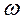 .
.
Другими словами, должны выполнятся условия
 (274)
(274)
и  (275)
(275)
Из (275) имеем два условия
 (276)
(276)
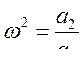 (277)
(277)
Подставляя эти значения в (274), получим для первого случая
 ,
,
а для второго –
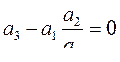
или  (278)
(278)
Возвращаясь к критериям устойчивости Гурвица, легко убедиться, что условие (178) выполняется, согласно уравнению (268), когда

В этом случае характеристическое уравнение (267) принимает вид
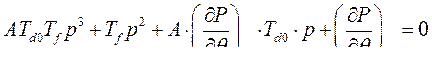 (279)
(279)
Для нахождения корней на границе устойчивости, уравнение (279) приведем к виду:

где
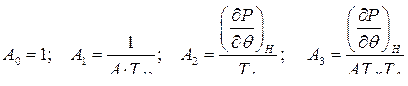 ,
,
а также используем теорему Виета для кубического уравнения:
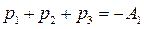 и
и 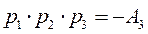 , следовательно,
, следовательно,
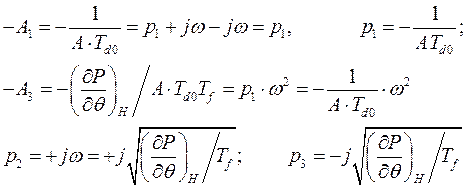
Система дифференциальных уравнений (266) относительно вариаций 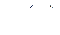 и
и 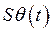 в предположении, что
в предположении, что  , разрешенная относительно
, разрешенная относительно 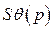 в операторной форме при условии, что на неё действует единичное импульсное воздействие, дает следующее
в операторной форме при условии, что на неё действует единичное импульсное воздействие, дает следующее
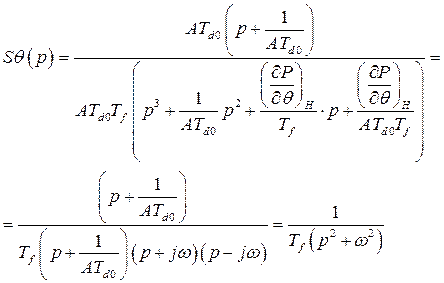 (280)
(280)
Воспользовавшись обратным преобразованием Лапласа, находим
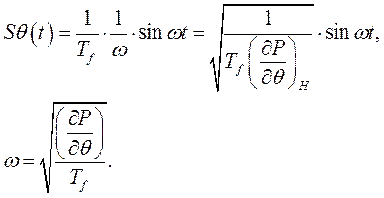 (281)
(281)
Другими словами, на границе устойчивости ротор генератора будет совершать колебания с постоянной амплитудой, рис. 34, а.
Согласно теореме о непрерывной зависимости корней алгебраического уравнения от его коэффициентов, которая утверждает, что при малом изменении коэффициентов уравнения мало меняются его корни, можно заключить, что когда условие
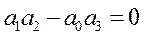
нарушается и эта разность становится меньше нуля, т.е.
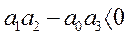
чему соответствует, как было показано выше, условие
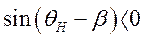
при переходе через нуль 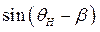 комплексные корни перестают быть чисто мнимыми и приобретают положительную вещественную составляющую. При этом, безусловно, изменится и мнимая составляющая. Пусть
комплексные корни перестают быть чисто мнимыми и приобретают положительную вещественную составляющую. При этом, безусловно, изменится и мнимая составляющая. Пусть 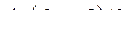 , но мало отличается от нуля по модулю. В этом случае корни характеристического уравнения можно представить в виде
, но мало отличается от нуля по модулю. В этом случае корни характеристического уравнения можно представить в виде

Решение системы однородных дифференциальных уравнений (265) относительно 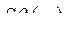 в операторной форме при нулевых начальных условиях дает
в операторной форме при нулевых начальных условиях дает
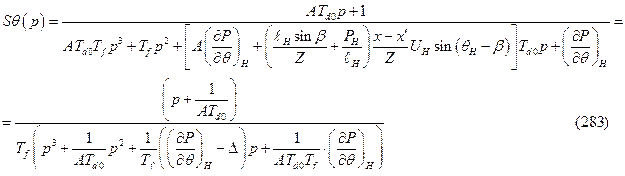
Здесь 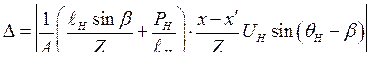
Характеристическим уравнением системы является
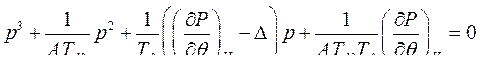
С его помощью возможно оценить как при этом изменится вещественный корень и мнимые части комплексных корней. По теореме Виета для кубического уравнения имеем:
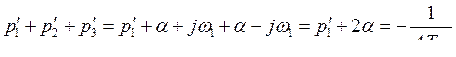
Откуда
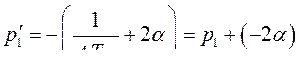 (284)
(284)
То – есть вещественный корень становится более отрицательным.
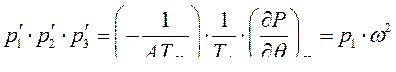
Или 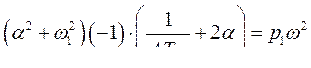
Откуда следует, что
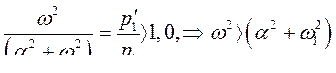
То – есть 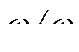 (285)
(285)
Это значит, что частота колебаний ротора по мере перехода в область неустойчивого режима уменьшается.
Уравнение (283) приводится к виду
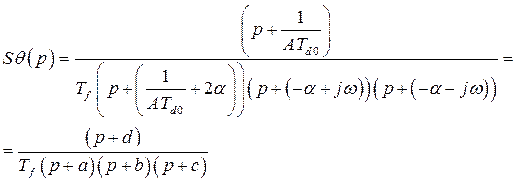 (286)
(286)
Используя обратное преобразование Лапласа, 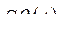 находим в виде
находим в виде
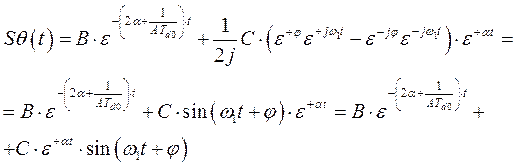 (287)
(287)
 здесь
здесь
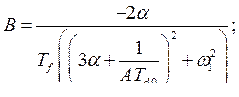
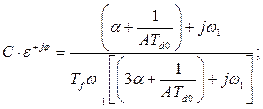
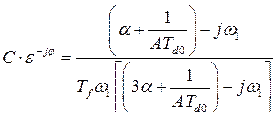
В этом случае раскачивание ротора сопровождается увеличением амплитуды отклонения угла 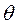 . Это может привести к выпадению генератора из синхронизма, рис. 34, б.
. Это может привести к выпадению генератора из синхронизма, рис. 34, б.
Статическая устойчивость системы синхронный генератор –
сеть при наличии АРВ у генератора.
1. регулирование возбуждения по отклонению напряжения генератора. Однолинейная схема, рис. 35, б.
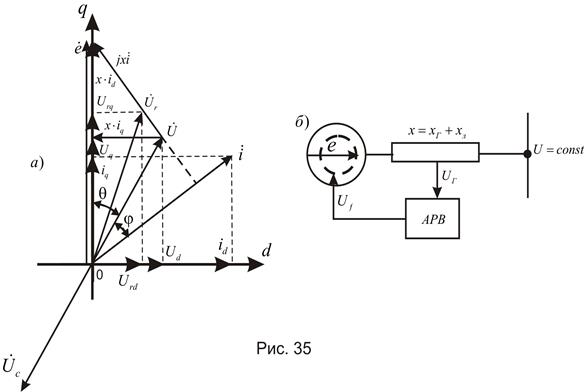
Закон регулирования возбуждения.
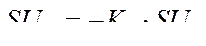
Принятые допущения: 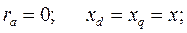
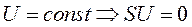
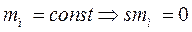
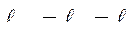
|
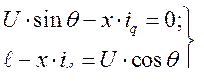
При записи уравнений электрического и механического состояния в вариациях принимаем обозначения:
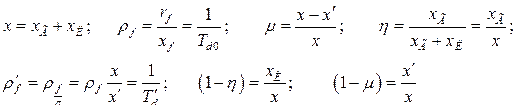
Исходная система уравнений
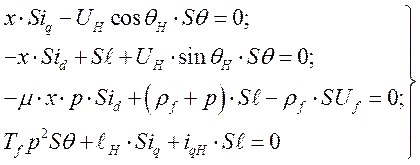 (288)
(288)
Вариацию напряжения генератора 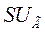 находим из следующих соображений
находим из следующих соображений
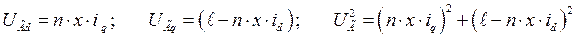
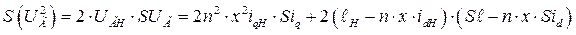
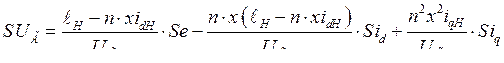 (289)
(289)
На основании закона регулирования возбуждения для 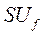 имеем:
имеем:
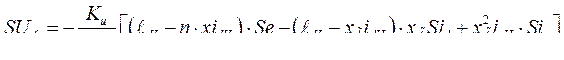
Из первых 2-х уравнений исходной системы (288) находим 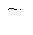 и
и 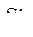
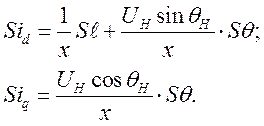
Подставив 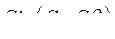 и
и  в уравнения цепи обмотки возбуждения и механического равновесия, получим:
в уравнения цепи обмотки возбуждения и механического равновесия, получим:
 (290)
(290)
В этих уравнениях

Приведем систему уравнений (290) к матричной форме записи
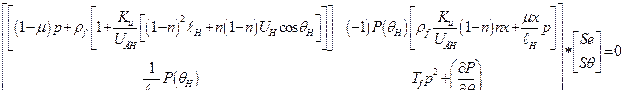
Если определитель данной матрицы приравнять к нулю, получим характеристическое уравнение, описывающее свободное движение системы. Найдем его.
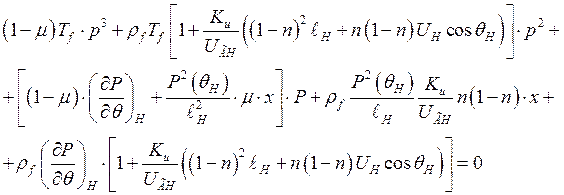
Или
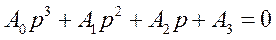 (291)
(291)
В этом уравнении
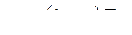
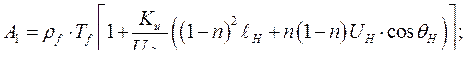
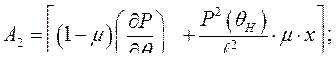
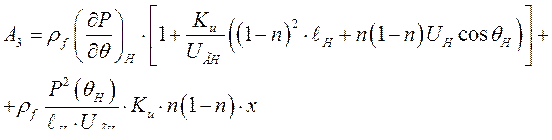
Так как характеристическое уравнение – уравнение 3-го порядка, проще всего для анализа устойчивости использовать критерий Гурвица. Определитель Гурвица для системы 3-го порядка
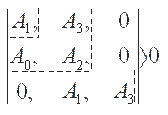
Для того, чтобы все корни характеристического уравнения были в левой части комплексной плоскости корней необходимо, чтобы определитель Гурвица и диагональные определители были положительны. В данном случае это требование сводится к условиям
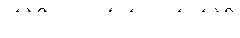 и
и 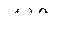
А. Условие 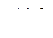
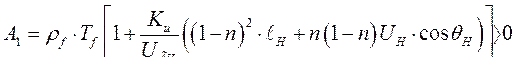
В генераторном режиме при 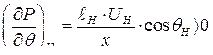 условие
условие 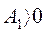 выполняется всегда, (т.к.
выполняется всегда, (т.к. 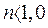 по определению) при
по определению) при 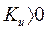 (отрицательная обратная связь по напряжению генератора). При отрицательном значении
(отрицательная обратная связь по напряжению генератора). При отрицательном значении 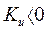 (положительная обратная связь по напряжению генератора) условие
(положительная обратная связь по напряжению генератора) условие 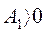 сводится к требованию
сводится к требованию
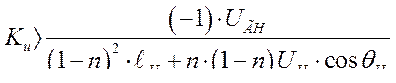 (292)
(292)
Или
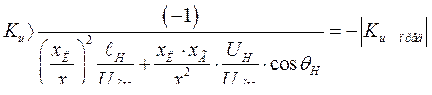
Графически
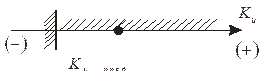
Б. условие  сводится к требованию
сводится к требованию
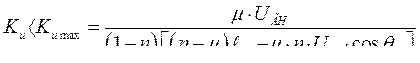 (293)
(293)
В. Условие 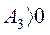 сводится к требованию
сводится к требованию
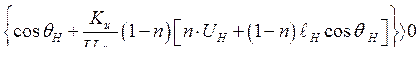 (294)
(294)
или
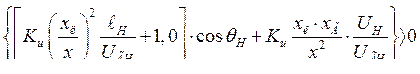 (295)
(295)
Из выражения (292) следует, что устойчивая параллельная работа генератора с сетью возможна даже при относительно небольшой положительной обратной связи по напряжению генератора при регулировании напряжения по отклонению регулируемой величины. Требования (294) и (295) взаимно противоречивы. Из выражения (294), характеризующего предельный угол устойчивой работы по «сползанию ротора», следует что 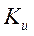 желательно брать как можно большим, т.к. при этом возрастает предельный угол
желательно брать как можно большим, т.к. при этом возрастает предельный угол 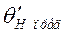 в области
в области 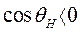 . Однако неравенство (294) ограничивает этот угол. С увеличением
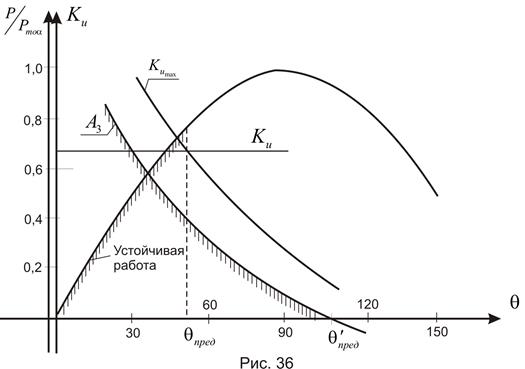
. Однако неравенство (294) ограничивает этот угол. С увеличением 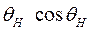 уменьшается, знаменатель в выражении
уменьшается, знаменатель в выражении 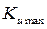 увеличивается, а максимально допустимый
увеличивается, а максимально допустимый  уменьшается.
уменьшается.
2. Регулирование напряжения по закону нормального компаундирования. Закон регулирования напряжения в о.е. имеет вид

Тоже в вариациях - 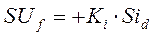 .
.
Основная система уравнений синхронной машины при неучете переходных колебаний в цепях якоря машины, а также при тех же допущениях и обозначениях, принятых в предыдущем параграфе,
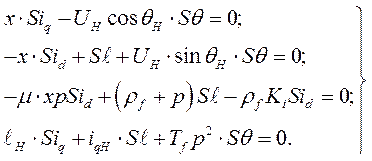 (296)
(296)
Разрешив данную систему уравнений относительно 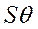 , находим
, находим
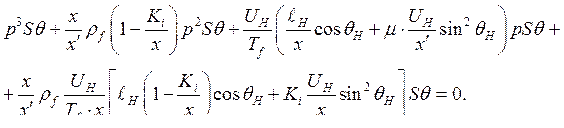
Характеристическое уравнение
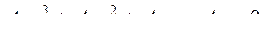
Где 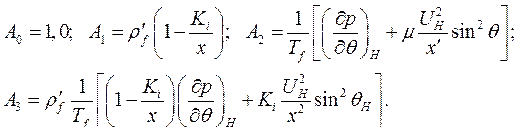
Воспользуемся критерием Гурвица для условий устойчивости.
1-е условие  при
при 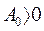
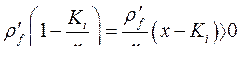 . Ввиду того, что
. Ввиду того, что  сводится к условию
сводится к условию
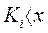 или
или 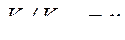 (297)
(297)
2-е условие 
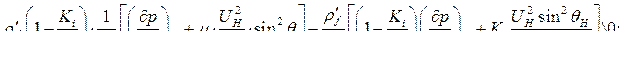
В виду 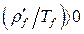 приводим к виду
приводим к виду
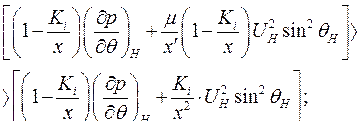
Так как 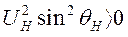 всегда, то неравенство сводится к
всегда, то неравенство сводится к
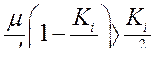 или
или
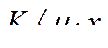 (298)
(298)
Так как 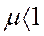 , то требование (298) более жесткое, чем требование (297).
, то требование (298) более жесткое, чем требование (297).
3-е условие 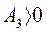 . Так как
. Так как 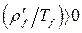 , условие сводится к требованию
, условие сводится к требованию
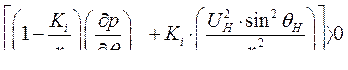 (299)
(299)
Если условие устойчивости по «сползанию ротора» выполняется, а именно:
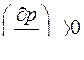 и выполняется условие
и выполняется условие
 то
то 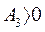 при всех углах
при всех углах 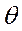 в пределах, при которых
в пределах, при которых 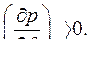 Таким образом, условие отсутствия самораскачивания ротора
Таким образом, условие отсутствия самораскачивания ротора
 (300)
(300)
Анализ устойчивости СГ при автономной работе на
нагрузку и регулирование возбуждения по принципу
фазового компаундирования.
1. Определение коэффициентов усиления.
Закон регулирования возбуждения запишем в виде
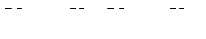
Здесь 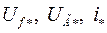 - соответственно напряжение на обмотке возбуждения, напряжение и ток нагрузки генератора в о.е.
- соответственно напряжение на обмотке возбуждения, напряжение и ток нагрузки генератора в о.е.
Э.д.с в фазе рабочей обмотки ТФК, как известно, равна
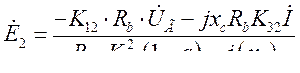 или
или
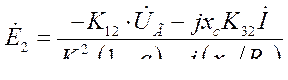
В этом выражении 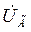 и
и 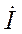 - комплексы действующих значений напряжения и тока фазы якоря СГ. Обозначив комплекс
- комплексы действующих значений напряжения и тока фазы якоря СГ. Обозначив комплекс  , запишем
, запишем  в о.е. Базисное напряжение цепи статора СГ
в о.е. Базисное напряжение цепи статора СГ 
Таким образом, имеем:
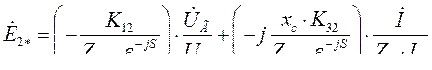
В виду того, что на обмотку напряжения подается выпрямленное напряжение,
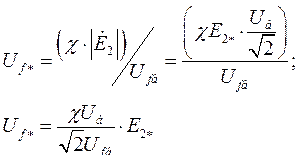
В последних выражениях появление 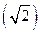 определяется тем, что в качестве базисных величин напряжения и тока приняты амплитудные значения фазных величин.
определяется тем, что в качестве базисных величин напряжения и тока приняты амплитудные значения фазных величин.
Обозначим 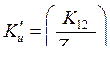 и
и 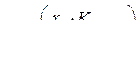
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|