
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Асинхронная машина. 11 страница
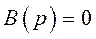 , совпадающие с корнями
, совпадающие с корнями 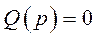 .
.
Действительно,
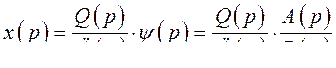 (376)
(376)
Если уравнение 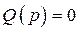 тождественно равно уравнению
тождественно равно уравнению 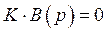 и все
и все 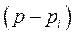 сократятся
сократятся
Уравнение (376) примет вид
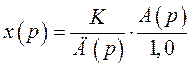
В результате в уравнении (374) исчезнет вторая сумма и ошибка будет иметь вид
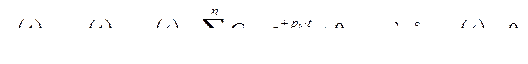
Рассмотрим некоторые способы достижения инвариантности к какому – либо входному воздействию.
1. Инвариантность к заданному воздействию
Исходная передаточная функция замкнутой системы, рис 41.
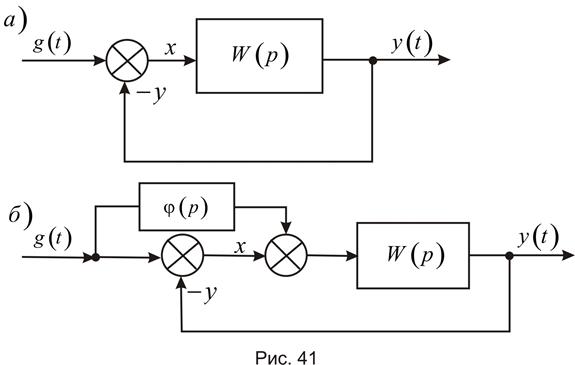
Замкнем сумматор главной обратной связи некоторой передаточной функцией 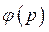 , рис. 41,б. В результате получим
, рис. 41,б. В результате получим
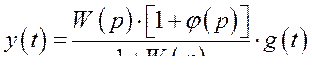 (377) или
(377) или 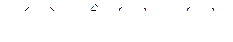
где 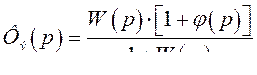 (378) эквивалентная передаточная функция замкнутой системы. Передаточная функция замкнутой системы по ошибке (334) имеет вид
(378) эквивалентная передаточная функция замкнутой системы. Передаточная функция замкнутой системы по ошибке (334) имеет вид
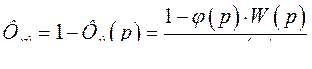 (379) а передаточная функция разомкнутой системы в соответствии с (335) будет
(379) а передаточная функция разомкнутой системы в соответствии с (335) будет
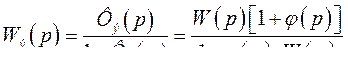 (380)
(380)
Положив 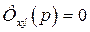 , находим условие полной инвариантности системы по
, находим условие полной инвариантности системы по 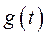 . Из (379) следует, что
. Из (379) следует, что 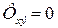 при
при
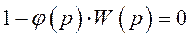 или
или
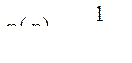 (381)
(381)
Разложив найденную 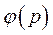 в ряд по возрастающим степеням
в ряд по возрастающим степеням 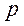 , получим необходимый вид функции, определяющий вводимый сигнал от управляющего воздействия
, получим необходимый вид функции, определяющий вводимый сигнал от управляющего воздействия
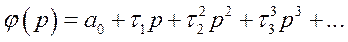 (382)
(382)
В некоторых случаях сигнал по задающему воздействию может вводится не непосредственно на вход системы, а в некоторую точку внутри канала управления, рис. 42.
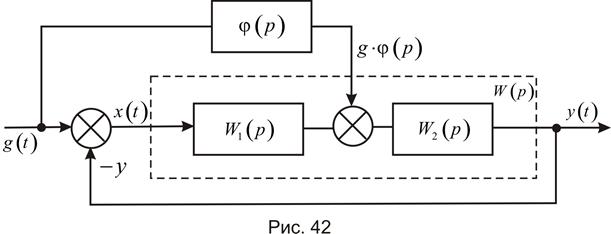
В данном случае 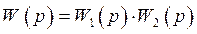 - передаточная функция разомкнутого канала управления и
- передаточная функция разомкнутого канала управления и

передаточная функция эквивалентной замкнутой системы. Соответственно передаточная функция эквивалентной замкнутой системы по ошибке
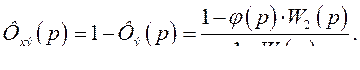 (383)
(383)
Откуда легко находим условие полной инвариантности по задающему воздействию
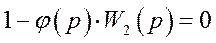 ,
,
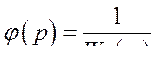 (384)
(384)
При этом эквивалентная передаточная функция разомкнутой системы (при размыкании главной обратной связи) будет иметь вид
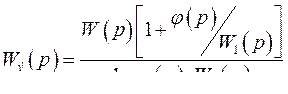 (385)
(385)
2. Инвариантность по отношению к возмущающему воздействию
Комбинированное управление используют с целью снижения ошибки от возмущающего воздействия, например, рис. 43.
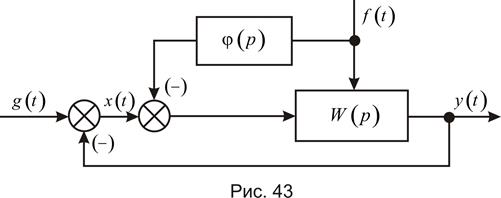
В этом случае наряду с регулированием по отклонению 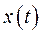 используется регулирование по возмущающему воздействию
используется регулирование по возмущающему воздействию 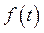 . Передаточная функция замкнутой системы по возмущающему воздействию будет иметь вид
. Передаточная функция замкнутой системы по возмущающему воздействию будет иметь вид
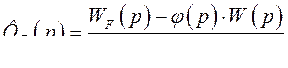 (386)
(386)
Где 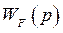 - передаточная функция по данному возмущению в разомкнутой системе;
- передаточная функция по данному возмущению в разомкнутой системе;
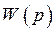 - передаточная функция разомкнутой системы.
- передаточная функция разомкнутой системы.
Действительно,
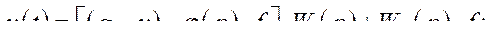
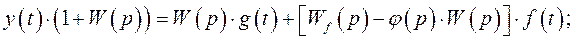
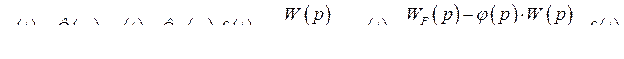
Условием полной инвариантности по возмущающему воздействию является равенство нулю 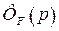 .
.
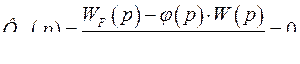 при
при
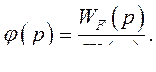 (387)
(387)
Эта функция может быть представлена в виде ряда, аналогично выражению (382)
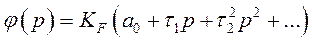 (388) где
(388) где 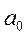 - безразмерное число (1 или 0), а
- безразмерное число (1 или 0), а 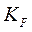 - некоторый коэффициент, размерность которого совпадает с размерностью передаточной функции.
- некоторый коэффициент, размерность которого совпадает с размерностью передаточной функции.
В отдельных случаях сигнал по возмущающему воздействию может вводиться не на вход системы, а в некоторую точку внутри канала регулирования, как показано на рис. 44.
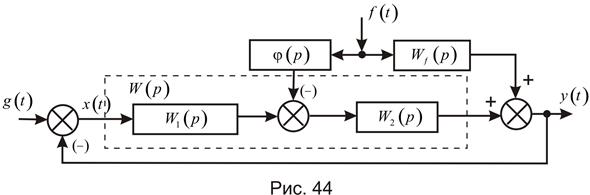
В соответствии со структурной схемой можно записать следующие выражения
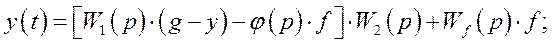
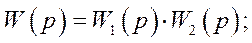
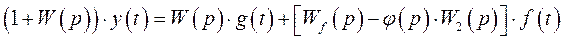 или
или
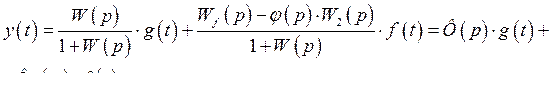 (389)
(389)
Полная инвариантность по возмущающему воздействию достигается при
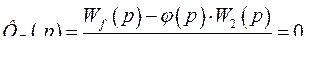
Откуда находим
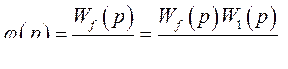 (390)
(390)
Как в случае регулирования по задающему воздействию, получение полной инвариантности затрудняется необходимостью вводить первую и более высокого порядка производные от возмущения  . Поэтому, как правило, реализуют частичную инвариантность, которая достигается за счет использования в системе регулирования первых членов разложения
. Поэтому, как правило, реализуют частичную инвариантность, которая достигается за счет использования в системе регулирования первых членов разложения 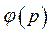 .
.
3. Неединичные обратные связи.
Неединичные обратные связи применяются для уменьшения ошибки, вызванной задающим воздействием в замкнутой системе регулирования. Рассмотрим структурную схему, рис. 45.
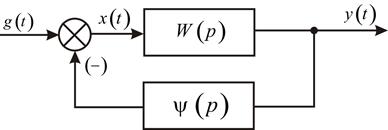
В этом случае регулируемая величина будет
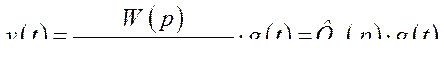
Передаточная функция замкнутой системы по ошибке
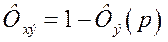
Для получения полной инвариантности необходимо выполнить условие
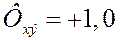
Отсюда легко найти вид требуемой передаточной функции 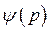

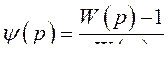 (391)
(391)
При разложении последнего выражения в степенной ряд получим
 (392)
(392)
Из выражения (392) видно, что для получения полной инвариантности необходимо использовать главную обратную связь с коэффициенту передачи отличным от единицы, 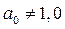 (в астатических системах
(в астатических системах  ) и дополнительно ввести положительные обратные связи по производным от регулируемой величины.
) и дополнительно ввести положительные обратные связи по производным от регулируемой величины.
Реализация полной инвариантности, т.е. условия (391) практически невозможна. Этому ряд причин: во – первых, невозможно точно ввести высшие производные, во – вторых, при выполнении условия (391) система будет находиться на границе устойчивости. Поэтому неединичные обратные связи используют лишь как средство повышение точности.
Покажем как это делается. Заменим реальную структурную схему с передаточной функцией 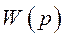 и неединичной обратной связью
и неединичной обратной связью 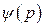 , рис. 45, на эквивалентную схему с единичной обратной связью и некоторой эквивалентной передаточной функцией разомкнутой системы
, рис. 45, на эквивалентную схему с единичной обратной связью и некоторой эквивалентной передаточной функцией разомкнутой системы 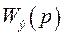 . Она находится из равенства
. Она находится из равенства
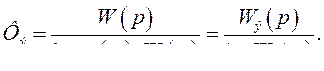
Это для 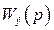 дает
дает
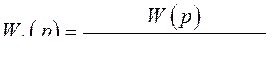 (393)
(393)
Действие неединичной обратной связи оказывается наиболее эффективным в статических системах. Здесь простым изменением коэффициента передачи жесткой главной обратной связи можно получить астатизм относительно управляющего воздействия. Рассмотрим пример. Пусть
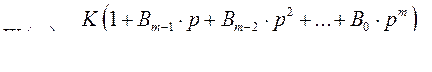 пусть
пусть 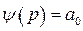 - жесткая главная обратная связь.
- жесткая главная обратная связь.
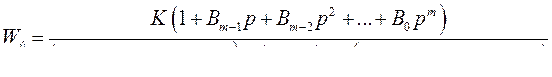
Нетрудно увидеть, что при условии
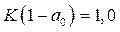 или
или 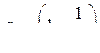
в знаменателе исчезает член с оператором в нулевой степени. В этом случае эквивалентная передаточная функция разомкнутой системы будет обладать астатизмом первого порядка.
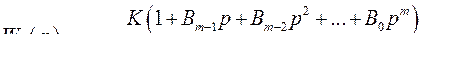 (394)
(394)
Эта система будет обладать добротностью по скорости
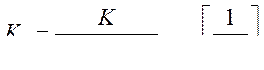 (395)
(395)
Таким образом, путем уменьшения коэффициента передачи в цепи главной обратной связи на незначительную по сравнению с единицей величину можно получить в системе астатизм первого порядка относительно задающего воздействия, что будет означать отсутствие статической ошибки и равенство нулю первого коэффициента ошибки, 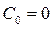 , смотри (362, 363)
, смотри (362, 363)
4. Масштабирование.
Следует заметить, что уничтожить статическую ошибку в статической системе можно путем масштабирования входной или выходной величины, как показано на рис. 46.
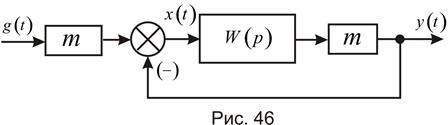
Если на входе или выходе системы включить масштабирующее устройство с коэффициентом передачи
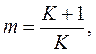
То регулируемая величина будет связана с задающим воздействием 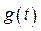 соотношением
соотношением
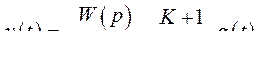
В установившемся режиме
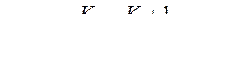
Что соответствует отсутствию статической ошибки.
Простейшая передаточная функция синхронной машины
в качестве объекта регулирования напряжения.
Рассмотрим уравнение электрического равновесия обмотки возбуждения синхронной машины
 (396)
(396)
Если в качестве единицы времени использовать радиан или синхронную секунду, уравнение (396) приводится к виду
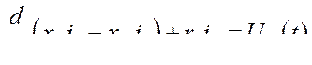 (397)
(397)
Умножим все компоненты уравнения (397) на 
Где 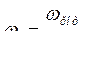 - отношение действительной скорости ротора генератора к синхронной.
- отношение действительной скорости ротора генератора к синхронной.
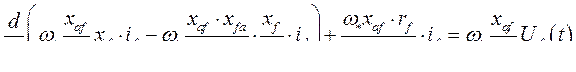
Преобразуем последнее выражение
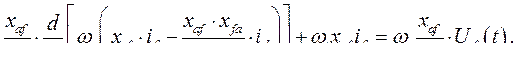 (398)
(398)
Но, с другой стороны, известно, что
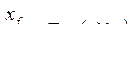 - постоянная времени обмотки возбуждения при разомкнутой якорной обмотке в радианах;
- постоянная времени обмотки возбуждения при разомкнутой якорной обмотке в радианах;
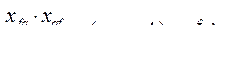 ;
;
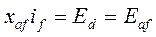 - полная э.д.с. синхронной машины, соответствующая
- полная э.д.с. синхронной машины, соответствующая 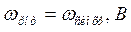 ;
;
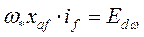 - та же э.д.с., но соответствующая действительной (текущей) скорости вращения ротора,
- та же э.д.с., но соответствующая действительной (текущей) скорости вращения ротора, 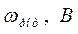 .
.
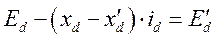 - э.д.с. СГ за переходной реактивностью при условии
- э.д.с. СГ за переходной реактивностью при условии 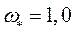 .
.
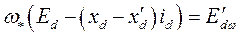 - э.д.с. СГ за переходной реактивностью при
- э.д.с. СГ за переходной реактивностью при 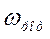 отличной от синхронной.
отличной от синхронной.
Таким образом, обозначая в дальнейшем действительные э.д.с. полную, 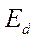 , и за переходной реактивностью,
, и за переходной реактивностью, 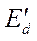 , с учетом скорости вращения ротора,
, с учетом скорости вращения ротора, 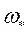 , имеем:
, имеем:
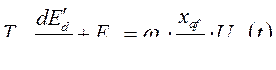 (399)
(399)
Запишем уравнение (399) в вариациях
 (400)
(400)
В большинстве случаев при анализе процесса регулирования возбуждения синхронного генератора изменением скорости ротора пренебрегают и считают 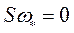 ,
, 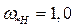 . И уравнение (400) принимает вид
. И уравнение (400) принимает вид
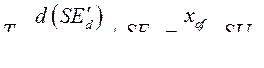 (401)
(401)
Для установления связи между 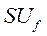 и
и 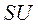 необходимо установить связь между напряжением
необходимо установить связь между напряжением 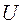 и э.д.с
и э.д.с 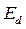 и
и 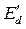 для некоторого конкретного режима.
для некоторого конкретного режима.
Рассмотрим векторную диаграмму явнополюсной синхронной машины, рис. 47.
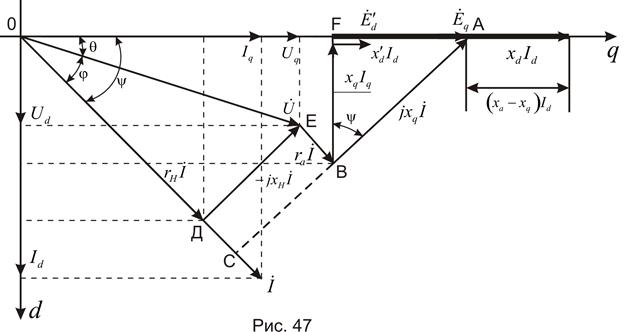
Введем следующие обозначения:

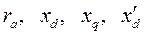 - параметры обмотки якоря генератора
- параметры обмотки якоря генератора
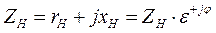 - полное (кажущееся) сопротивление нагрузки;
- полное (кажущееся) сопротивление нагрузки;
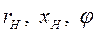 - его активная и реактивная компоненты и аргумент.
- его активная и реактивная компоненты и аргумент.
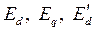 - э.д.с. соответственно, полная, за поперечной реактивностью и за переходной реактивностью.
- э.д.с. соответственно, полная, за поперечной реактивностью и за переходной реактивностью.
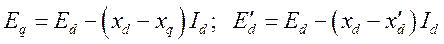
В соответствии с векторной диаграммой можно записать следующие уравнения:
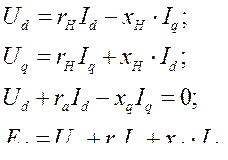
Приравнивая 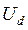 и
и 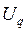 из первой и второй пары уравнений, находим
из первой и второй пары уравнений, находим
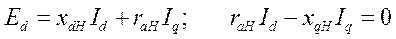
Последнее уравнение дает
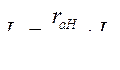 и
и
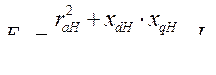 ,
,
Что позволяет выразить ток  через
через 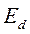
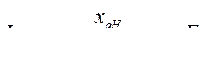
Треугольник ОАС векторной диаграммы является прямоугольным. Гипотенуза этого треугольника ОА равна э.д.с. за поперечной реактивностью, 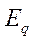 ; катет ОС в масштабе напряжения равен
; катет ОС в масштабе напряжения равен 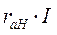 , а катет АС -
, а катет АС - 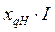 таким образом
таким образом

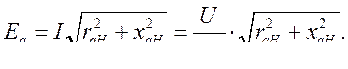
Выразим  через
через 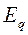
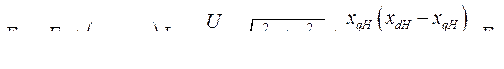 или
или
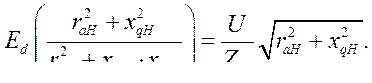
Окончательно имеем:
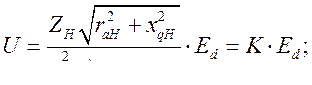 (402)
(402)
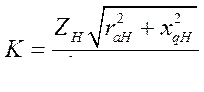 (403)
(403)
Аналогично можно выразить напряжение,  , через параметры генератора и нагрузки и э.д.с. за переходной реактивностью,
, через параметры генератора и нагрузки и э.д.с. за переходной реактивностью, 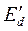 .
.
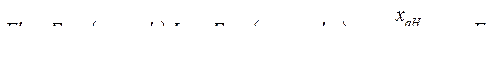
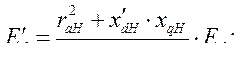 (404)
(404)

Подставив 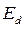 в выражение (405), находим:
в выражение (405), находим:
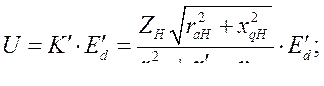 (406)
(406)
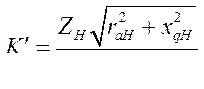 (407)
(407)
Для некоторой конкретной нагрузки можно записать
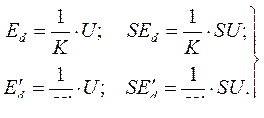 (408)
(408)
В уравнениях (399), (400), (401) выразим 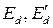 ,
, 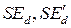 через напряжение,
через напряжение, 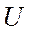 , используя равенства (408).
, используя равенства (408).
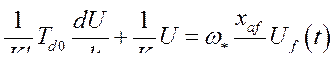 или
или
 обозначим
обозначим  - постоянная времени обмотки возбуждения с учетом взаимоиндукции с обмоткой якоря (статора) машины при замыкании последней на некоторую конкретную нагрузку. Следует напомнить, что при переходе к новой нагрузке эта постоянная времени будет изменяться. Итак, имеем:
- постоянная времени обмотки возбуждения с учетом взаимоиндукции с обмоткой якоря (статора) машины при замыкании последней на некоторую конкретную нагрузку. Следует напомнить, что при переходе к новой нагрузке эта постоянная времени будет изменяться. Итак, имеем:
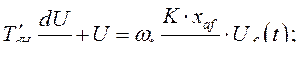 (409)
(409)
 (410)
(410)
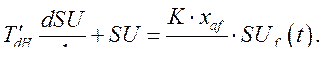 (411)
(411)
Запишем последнее уравнение в операторной форме, обозначив
 - оператор дифференцирования по синхронному времени,
- оператор дифференцирования по синхронному времени,
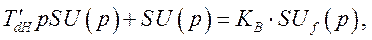 где
где 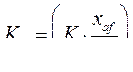 .
.
Или

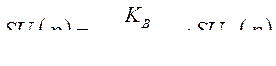 (412)
(412)
Простейшая передаточная функция синхронной машины как объекта регулирования напряжения.
Ей соответствует структурная схема
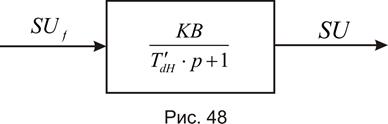
Легко трансформировать уравнение (401) таким образом, чтобы в передаточную функцию входили ток нагрузки 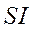 или его производная
или его производная 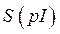 или же та и другая величина одновременно. Если в уравнении (401) э.д.с.
или же та и другая величина одновременно. Если в уравнении (401) э.д.с. 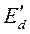 выразить в виде
выразить в виде
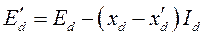 , соответственно
, соответственно
 (413)
(413)
Затем проделать преобразования аналогичные сделанным выше, получим
 (414)
(414)
Чему соответствует структурная схема
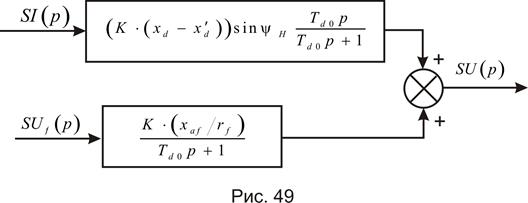
Если же в уравнение (401) вариацию э.д.с. 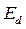 представить в виде
представить в виде
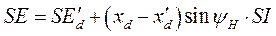 и проделать аналогичные преобразования, получим:
и проделать аналогичные преобразования, получим:
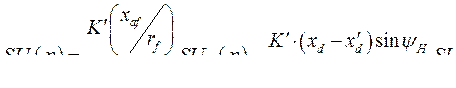 (415)
(415)
Структурная схема изображена на рис. 50.
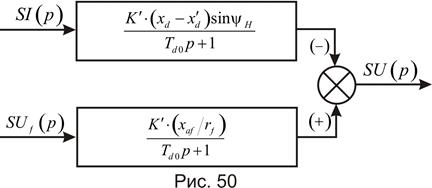
Не будет лишним напомнить, что входящие в выражения (413) и (414) и структурные схемы
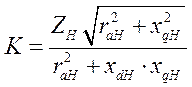 и
и  .
.
Передаточные функции и структурные схемы
синхронного генератора в качестве объекта
регулирования напряжения.
Предварительные замечания. Ввиду того, что постоянные времени обмотки статора на один – два порядка меньше постоянной времени обмотки возбуждения переходными процессами в цепях якоря пренебрегаем, т.е. считаем, что при изменении координат цепи ротора, координаты статорной обмотки устанавливаются мгновенно. Это позволяет соотношения между токами, э.д.с. и напряжением цепи якоря определять непосредственно из векторной диаграммы. Активное сопротивление фазы обмотки якоря в сотню раз меньше её реактивностей. Поэтому им тоже можно пренебречь. Рассмотрение начнем с наиболее простого случая, неявнополюсной синхронной машины. Её векторная диаграмма представлена на рис. 51.

У этой машины 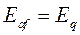 ,
,  ;
; 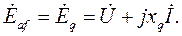 рассматривая треугольник ОАВ на векторной диаграмме и используя теорему косинусов, имеем:
рассматривая треугольник ОАВ на векторной диаграмме и используя теорему косинусов, имеем:
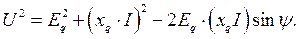 (416)
(416)
Перепишем уравнение (416) в вариациях, считая что характер нагрузки не меняется.
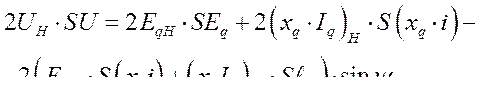 (417)
(417)
Разрешим уравнение (417) относительно вариации 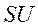
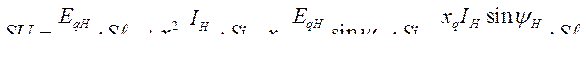
Объединим составляющие, содержащие  и
и 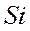
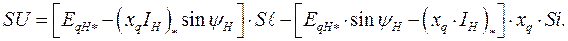
Здесь 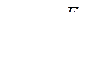 и
и 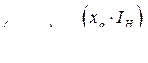 -
-
Значения соответственно э.д.с. и падения напряжения на реактивности 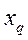 , отнесенные к начальному напряжению.
, отнесенные к начальному напряжению.
Из векторной диаграммы, рис. 51, следует, что
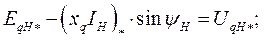
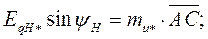
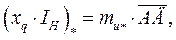 следовательно,
следовательно,
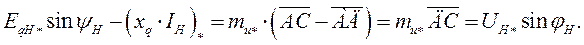
Все вышесказанное позволяет записать
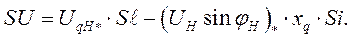 (418)
(418)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|