
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Асинхронная машина. 14 страница
Элементы уравнения моментов делим на
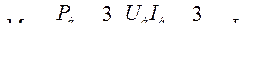
В результате имеем
 или
или
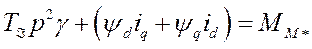 (480) где
(480) где 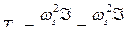 - инерционная постоянная времени агрегатов (в синхронных секундах);
- инерционная постоянная времени агрегатов (в синхронных секундах);
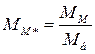
Сведя уравнения (476) – (480) в единую систему, получим уравнения синхронной машины в переменных  , записанные в о.е.:
, записанные в о.е.:
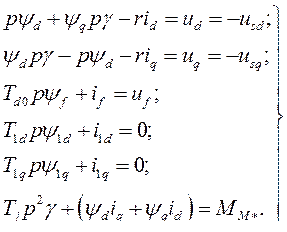 (481)
(481)
Уравнения синхронной машины в переменных 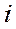 и
и 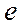 ,
,
записанные в о.е.
Чтобы получить уравнения синхронной машины в переменных 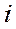 и
и 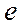 , необходимо, прежде всего, выразить её потокосцепления через токи контуров и реактивности машины.
, необходимо, прежде всего, выразить её потокосцепления через токи контуров и реактивности машины.
Потокосцепления статорной обмотки по продольной оси ротора в о.е.
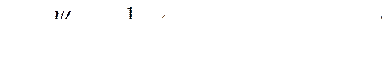 (482)
(482)
Аналогично для потокосцепления статорной обмотки по поперечной оси ротора в о.е. имеем
 (483)
(483)
Базисное потокосцепление 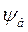 можно выразить следующими формулами:
можно выразить следующими формулами:
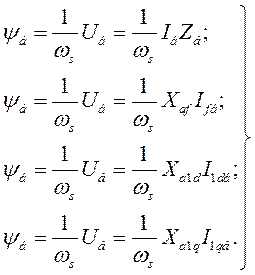 (484)
(484)
Формулы системы (484) позволяют уравнения (482) и (483) преобразовать к виду:
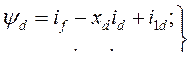 (485) где
(485) где
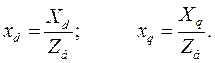
Потокосцепление обмотки возбуждения в о.е.
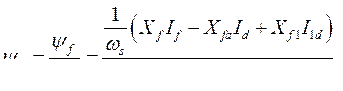 (486)
(486)
В свою очередь, потокосцепление 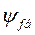 можно представить выражениями:
можно представить выражениями:
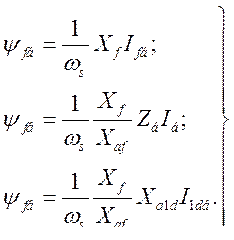 (487)
(487)
Используя (487), уравнение (486) приведем к виду
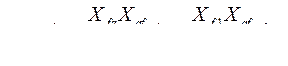 (488)
(488)
Реактивности, входящие в уравнение (488), можно преобразовать следующим образом:
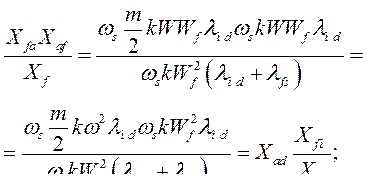
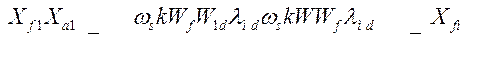
При приведении всех реактивностей к общему базису 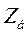 имеем:
имеем:
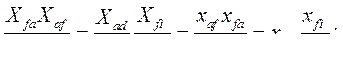
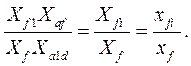
Таким образом, потокосцепление обмотки возбуждения в о.е.
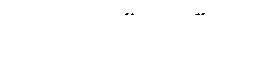
Реактивности 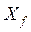 и
и  отличаются только магнитной проводимостью потокам рассеяния обмотки возбуждения. Действительно,
отличаются только магнитной проводимостью потокам рассеяния обмотки возбуждения. Действительно,
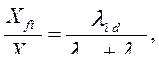 где
где 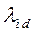 - магнитная проводимость потоку взаимной индукции по продольной оси ротора машины;
- магнитная проводимость потоку взаимной индукции по продольной оси ротора машины;
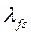 - магнитная проводимость потоку рассеяния обмотки возбуждения.
- магнитная проводимость потоку рассеяния обмотки возбуждения.
Обозначим через 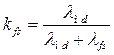 коэффициент, учитывающий рассеяние потока обмотки возбуждения. Это позволит записать потокосцепление обмотки возбуждения в о.е. в виде
коэффициент, учитывающий рассеяние потока обмотки возбуждения. Это позволит записать потокосцепление обмотки возбуждения в о.е. в виде
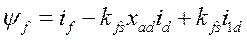 (489)
(489)
Тот факт, что токи обмотки возбуждения и успокоительных обмоток 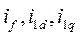 в выражения для потокосцеплений статорных обмоток
в выражения для потокосцеплений статорных обмоток 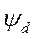 и
и 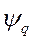 входят с коэффициентом пропорциональности, равным единице, позволяет утверждать, что эти токи в о.е. численно равны э.д.с. в о.е., наведенным в статорных обмотках потоками соответствующих обмоток ротора, т.е.
входят с коэффициентом пропорциональности, равным единице, позволяет утверждать, что эти токи в о.е. численно равны э.д.с. в о.е., наведенным в статорных обмотках потоками соответствующих обмоток ротора, т.е.
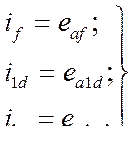 (490)
(490)
Заметим, что при отсутствии продольного успокоительного контура
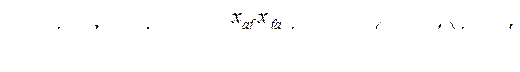 (491) т.е. потокосцепление обмотки возбуждения в о.е. численно равно э.д.с. машины за переходной реактивностью в о.е.
(491) т.е. потокосцепление обмотки возбуждения в о.е. численно равно э.д.с. машины за переходной реактивностью в о.е.
Выражение (491) имеет глубокий физический смысл и широко используется при анализе переходных режимов в системах с синхронными машинами. Действительно, благодаря значительной индуктивности обмотки возбуждения, её потокосцепление изменяется значительно медленнее, чем протекают переходные процессы в статорных цепях. Поэтому при решении целого ряда задач можно положить 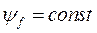 , а следовательно, и
, а следовательно, и 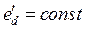 .
.
Потокосцепление успокоительной обмотки по продольной оси ротора в о.е.
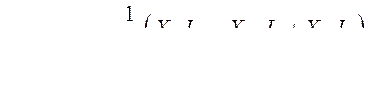
Учитывая, что 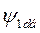 можно выразить как
можно выразить как
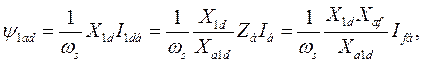 потокосцепление
потокосцепление 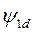 записываем в виде
записываем в виде
 (492)
(492)
Преобразуем сомножители перед 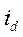 и
и 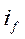 в выражении (492):
в выражении (492):
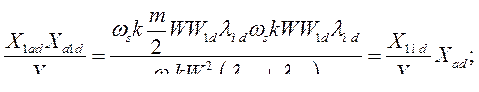
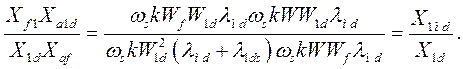
Приводя все реактивности к общему базису 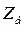 и вводя коэффициент, учитывающий рассеяние потока продольной успокоительной обмотки,
и вводя коэффициент, учитывающий рассеяние потока продольной успокоительной обмотки,
 для потока
для потока 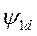 получаем выражение
получаем выражение
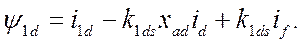 (493)
(493)
Аналогичным образом находим выражение для потокосцепления успокоительного контура по поперечной оси:
 (494) где
(494) где 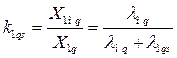 - коэффициент, учитывающий рассеяние потока успокоительной обмотки по поперечной оси ротора.
- коэффициент, учитывающий рассеяние потока успокоительной обмотки по поперечной оси ротора.
Объединяя выражения (485), (489), (493), (494) и принимая во внимание (490), запишем систему уравнений для потокосцеплений машины в о.е.
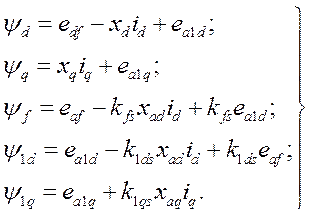 (495)
(495)
Для получения уравнений синхронной машины в переменных 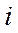 и
и 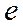 , записанных в о.е., вводим потокосцепления из системы (495) в уравнения системы (481):
, записанных в о.е., вводим потокосцепления из системы (495) в уравнения системы (481):
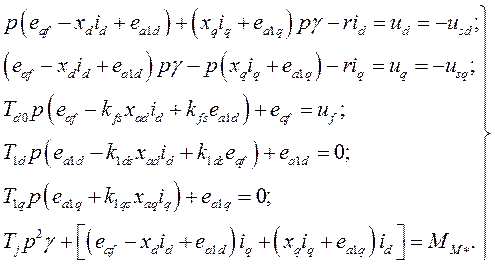 (496)
(496)
Уравнения синхронной машины без успокоительных контуров получаются из (496), положив в уравнениях оставшихся контуров 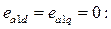
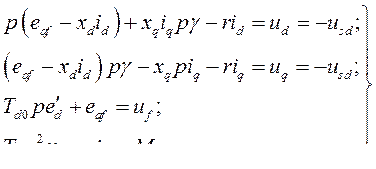 где
где 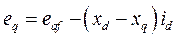 э.д.с. машины за поперечной реактивностью.
э.д.с. машины за поперечной реактивностью.
Уравнения синхронной машины.
Уравнения электрических контуров асинхронной машины, так же как и уравнения синхронной машины, могут быть получены из общего уравнения для любого контура электрической машины
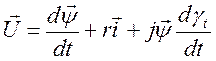 где
где 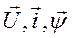 - изображающие векторы многофазных систем напряжений, токов и потокосцеплений;
- изображающие векторы многофазных систем напряжений, токов и потокосцеплений;
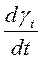 - мгновенная скорость вращения выбранных координатных осей.
- мгновенная скорость вращения выбранных координатных осей.
Проектируя изображающие векторы на ортогональные оси 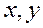 , вращающиеся с произвольной скоростью
, вращающиеся с произвольной скоростью  относительно фазных осей статора, а также учитывая, что в общем случае ротор вращается относительно статора со скоростью
относительно фазных осей статора, а также учитывая, что в общем случае ротор вращается относительно статора со скоростью 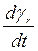 , уравнения электрического равновесия статорных и роторных цепей асинхронной машины запишем в виде:
, уравнения электрического равновесия статорных и роторных цепей асинхронной машины запишем в виде:
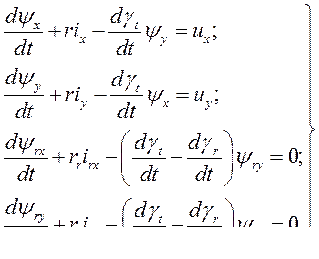
Уравнение моментов можно представить формулой
 где
где 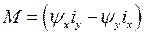 - электромагнитный момент
- электромагнитный момент
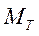 - тормозной момент.
- тормозной момент.
Метод составления уравнений СЭС.
Имея дифференциальные уравнения отдельных элементов электроэнергетической установки, можно составить общую систему уравнений, описывающих установившиеся и переходные режимы СЭС.
В качестве основной схемы замещения примем схему, состоящую из двух генераторов, работающих параллельно на комплексную нагрузку, состоящую из приводов с асинхронными двигателями и статической нагрузки рис. 63
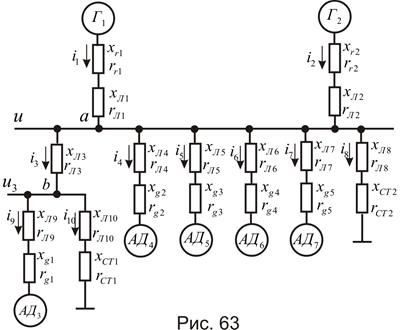
Если система включает в себя больше двух генераторов, то её, как правило, приводят к схеме замещения из двух генераторов. Асинхронную нагрузку с многочисленными двигателями заменяют одним – тремя эквивалентными двигателями 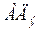 , включающими в себя приводы, близкие друг к другу по параметрам и характеристикам, а также исследуемый привод
, включающими в себя приводы, близкие друг к другу по параметрам и характеристикам, а также исследуемый привод 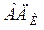 , поведение которого представляет особый интерес в переходных режимах СЭС.
, поведение которого представляет особый интерес в переходных режимах СЭС.
Полная система уравнений, описывающая переходные режимы в СЭС, представленной на рис. 63, включает в себя уравнения:
а) синхронных генераторов;
б) асинхронных двигателей;
в) статической нагрузки;
г) регулирования напряжения;
д) регулирования вращающих и тормозных моментов;
е) связи;
ж) фидеров схемы распределения.
Дифференциальные уравнения синхронных генераторов записываются с учетом параметров системы (соединительного кабеля и ГРЩ) до точки присоединения эквивалентной нагрузки.
Дифференциальные уравнения асинхронных двигателей вводятся также с учетом параметров сети до точки присоединения фидера к шинам ГРЩ. Моменты сопротивления на валах приводов принимаются в соответствии с характером приводов.
Уравнения статической нагрузки, как и уравнения генераторов и двигателей, записываются во вращающихся координатных осях. Аналогичные выражения получаются и для фидеров.
Уравнения автоматического регулирования возбуждения генераторов и скорости первичных двигателей записываются с учетом типа соответствующего регулятора. Наконец, уравнения связи определяют собой условия баланса мощности в точке присоединения нагрузки.
Перед составлением общей системы уравнений СЭС необходимо установить, в каких осях целесообразно записать уравнения отдельных элементов СЭС.
Выбор системы вращающихся координатных осей.
При выборе вращающихся координатных осей руководствуются принципом максимального упрощения всей системы уравнений, описывающих переходные режимы СЭС.
При этом уравнения для отдельного элемента системы могут быть представлены и не в простейшем виде. Однако совокупность уравнений синхронных машин, асинхронной и статической нагрузки должна быть наиболее простой, т.е. должна содержать минимальное число периодических коэффициентов, а также членов, характеризующих э.д.с. вращения.
Для решения указанного вопроса отметим особенности преобразованных по Гореву – Парку уравнений СЭС.
1. Периодические коэффициенты в уравнениях машин переменного тока с магнитной и электрической асимметрией (явнополюсные синхронные машины) или только с электрической асимметрией (неявнополюсные синхронные машины) исчезают лишь при записи их в координатах 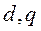 , жестко связанных с роторами соответствующих синхронных машин.
, жестко связанных с роторами соответствующих синхронных машин.
2. Периодические коэффициенты в уравнениях машин с магнитной и электрической асимметрией (асинхронные машины) исчезают при записи их в осях 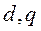 , вращающихся с любой скоростью.
, вращающихся с любой скоростью.
3. Периодические коэффициенты в уравнениях статических элементов отсутствуют. Однако при использовании вращающихся координатных осей 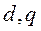 появляются дополнительные э.д.с. вращения, которые исчезают только при скорости вращения осей, равной нулю.
появляются дополнительные э.д.с. вращения, которые исчезают только при скорости вращения осей, равной нулю.
Отметим также специфические особенности судовых энергетических систем, которые необходимо учитывать при выборе систем координат:
а) отсутствие длинных линий и связанных с ними многочисленных статических элементов замещения;
б) радиальные сети СЭС;
в) незначительное число статических потребителей;
г) значительное число асинхронных двигателей.
Указанные особенности преобразований и самой СЭС дают основание утверждать, что определяющим элементом при выборе рациональной системы координат для записи уравнений судовых установок является синхронная машина.
Уравнения синхронных машин должны быть записаны в осях 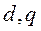 , жестко связанных с роторами соответствующих машин.
, жестко связанных с роторами соответствующих машин.
Это обстоятельство позволяет однозначно решить вопрос о нецелесообразности введения синхронных машин СЭС ни в общих координатных осях 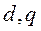 , вращающихся с синхронной скоростью, ни в координатных осях
, вращающихся с синхронной скоростью, ни в координатных осях 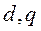 , жестко связанных с одной из синхронных машин.
, жестко связанных с одной из синхронных машин.
Уравнения всех асинхронных двигателей целесообразно отнести к координатным осям одной из синхронных машин. Число периодических коэффициентов при этом не изменится, но уравнения связи окажутся простыми, так как переменные всех асинхронных машин и одной синхронной машины будут записаны в одних и тех же осях и составляющие по ним могут алгебраически складываться.
Только переменные второго генератора в этом случае в уравнениях связи нужно будет привести к выбранным осям.
По тем же соображениям целесообразно отнести к осям того же генератора и уравнения статической нагрузки и фидеров.
Таким образом, уравнения СЭС, кроме уравнений второго генератора, оказываются записанными в осях одного из генераторов системы. При этом для асинхронной и статической нагрузки они выступают как оси, вращающиеся с произвольной скоростью. Это, между прочим, означает, что уравнения статической нагрузки становятся нелинейными ( 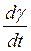 - величина переменная), и в этом отношении уравнения усложняются. В целом же они представляются в более простом варианте.
- величина переменная), и в этом отношении уравнения усложняются. В целом же они представляются в более простом варианте.
Действительно, если отнести и уравнения второго генератора к осям, жестко связанным с ротором первого генератора, то эти уравнения будут усложнены. Если же все уравнения записать в синхронных осях, то будут сложнее уравнения всех генераторов, хотя пропадут нелинейности в уравнениях статической нагрузки.
Общая система уравнений.
Составим общую систему уравнений СЭС, схема которой представлена на рис. 63. При этом используем соображения относительно рациональной записи уравнений. Уравнения нулевой последовательности опускаем. Уравнения синхронных генераторов записываем в осях 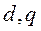 , жестко связанных с соответствующим ротором. Таким образом, имеем:
, жестко связанных с соответствующим ротором. Таким образом, имеем:
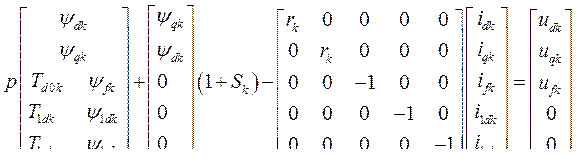 (497)
(497)
Здесь 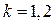 . Индекс 1 относится к первому генератору, индекс 2 – ко второму генератору;
. Индекс 1 относится к первому генератору, индекс 2 – ко второму генератору; 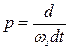 - символ дифференцирования по синхронному времени.
- символ дифференцирования по синхронному времени.
Рассмотрим следующие координатные оси (рис. 64):
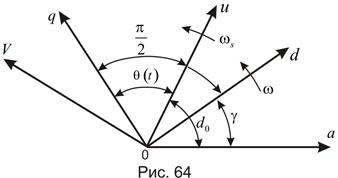
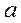 - неподвижная ось фазы обмотки статора синхронного генератора;
- неподвижная ось фазы обмотки статора синхронного генератора;
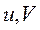 - система ортогональных осей, вращающихся с синхронной скоростью
- система ортогональных осей, вращающихся с синхронной скоростью 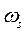 ;
;
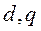 - система ортогональных осей, жестко связанных с ротором синхронного генератора и вращающихся с угловой частотой вращения ротора
- система ортогональных осей, жестко связанных с ротором синхронного генератора и вращающихся с угловой частотой вращения ротора 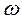 ;
;
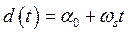 - угол между осью
- угол между осью 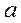 и осью
и осью 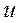 , вращающейся синхронно;
, вращающейся синхронно;
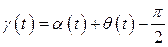 - угол между неподвижной осью
- угол между неподвижной осью 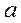 и осью
и осью 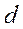 , продольной осью ротора синхронной машины;
, продольной осью ротора синхронной машины;
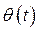 - угол между
- угол между 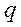 системы
системы 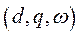 и
и 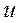 системы
системы  .
.
Таким образом,

Мгновенное значение угловой скорости ротора
 (498)
(498)
Скольжение ротора синхронного генератора относительно синхронных осей 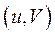 определим как
определим как
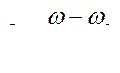 т.е. скольжение положительно при
т.е. скольжение положительно при  .
.
Разделив почленно уравнение (498) на 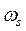 , а также учитывая, что
, а также учитывая, что 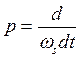 , получаем
, получаем
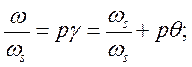 (499)
(499)
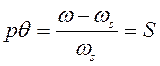 или
или
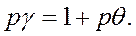 (500)
(500)
Из выражения (500), принимая во внимание (499), находим
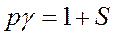 .
.
Таким образом, в уравнении (497)
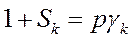 .
.
Напряжение на зажимах цепи возбуждения генератора 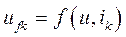 определяется законом регулирования возбуждения генератора.
определяется законом регулирования возбуждения генератора.
Связь между потокосцеплениями и токами синхронной машины выражается следующим уравнением:
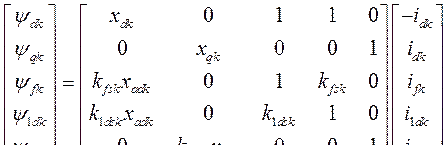 (501)
(501)
Уравнение моментов синхронных машин имеет вид
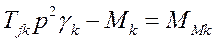 где
где
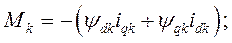
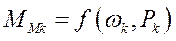 (502)
(502)
Выражение (502) определяется законом регулирования частоты и активной мощности первичного двигателя синхронного генератора.
Уравнения асинхронных двигателей записываем в координатных осях первого синхронного генератора, т.е. полагаем 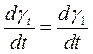 :
:
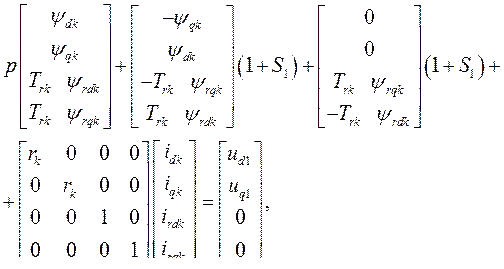 (503) где
(503) где 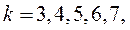 - индексы соответствующих асинхронных двигателей, эквивалентных и исследуемых:
- индексы соответствующих асинхронных двигателей, эквивалентных и исследуемых:

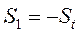 - скольжение первого генератора;
- скольжение первого генератора;

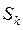 - скольжение соответствующего двигателя;
- скольжение соответствующего двигателя;
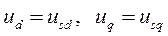 - напряжение генератора, являющиеся для асинхронного двигателя напряжением сети.
- напряжение генератора, являющиеся для асинхронного двигателя напряжением сети.
Потокосцепления обмоток асинхронных двигателей выражаются через соответствующие токи обмоток и реактивности с помощью следующего уравнения:
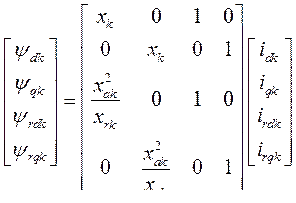
Уравнение моментов асинхронных двигателей имеет вид
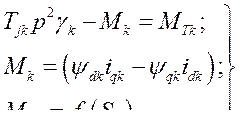
Уравнение статической нагрузки в соответствии с высказанными выше соображениями записываем в осях 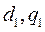 первого синхронного генератора, при этом
первого синхронного генератора, при этом 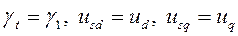 :
:
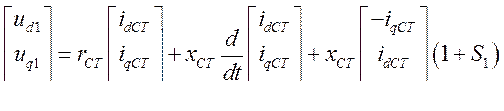 .
.
Уравнения связи могут быть составлены как баланс активной и реактивной мощностей в точке присоединения нагрузки:
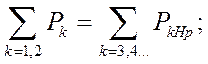
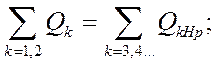 что в конечном счете (учитывая равенство напряжений со стороны источников и со стороны приемников в точке подключения нагрузки) эквивалентно уравнению первого закона Кирхгофа для узловой точки.
что в конечном счете (учитывая равенство напряжений со стороны источников и со стороны приемников в точке подключения нагрузки) эквивалентно уравнению первого закона Кирхгофа для узловой точки.
В соответствии с принятыми направлениями токов в схеме рис. 63 в фазных координатах имеем:
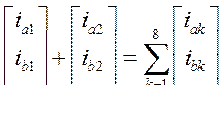
С равным успехом уравнение первого закона Кирхгофа может быть записано для проекций и.в. соответствующих токов.
Однако в этом случае проекции изображающих векторов должны быть взяты на одни и те же координатные оси.
Удобнее всего в качестве этих осей выбрать оси 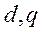 первого генератора.
первого генератора.
Для этого достаточно привести проекции и.в. тока только второго генератора к осям первого, так как уравнения всех остальных элементов системы записаны в осях первого генератора.
В результате получаем:
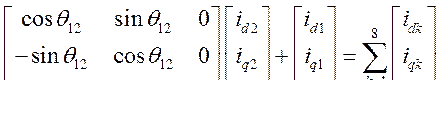 (504)
(504)
Смысл последнего преобразования (без токов нулевой последовательности) ясно виден из рис. 65
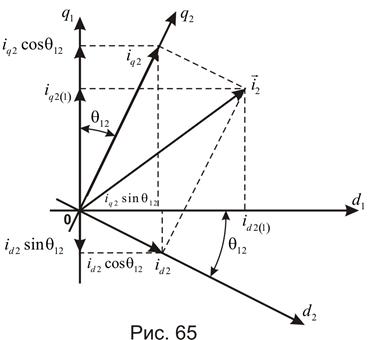
Так как вектор 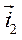 равен геометрической сумме своих проекций на оси
равен геометрической сумме своих проекций на оси 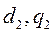 , то его проекция на ось
, то его проекция на ось 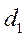 равна сумме проекций составляющих на ось
равна сумме проекций составляющих на ось 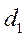 ; аналогично проекция
; аналогично проекция 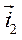 на ось
на ось 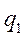 равна алгебраической сумме проекций составляющих по осям
равна алгебраической сумме проекций составляющих по осям 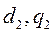 на ось
на ось 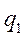 , т.е.
, т.е.

Таким же образом записываются выражения для напряжений:
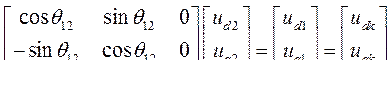 (505)
(505)
Рассматривая фидеры как статическую нагрузку, получим их уравнения:
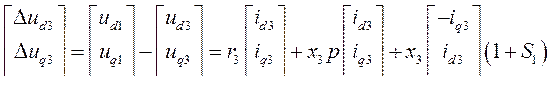 (506)
(506)
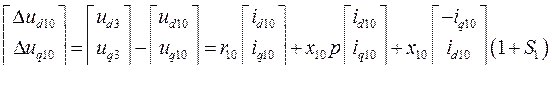 (507)
(507)
Наконец, уравнения в точке 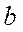 имеют вид
имеют вид
 (508)
(508)
Система уравнений (497), (501), (504), (505) – (508) описывает переходные процессы в судовой электроэнергетической установке, схема замещения которой показана на рис. 63.
Легко заметить, что приведение всей нагрузки к осям одного из генераторов позволило за счет некоторого усложнения уравнения статической нагрузки и уравнений связи генераторов записать уравнения обоих генераторов без периодических коэффициентов, что, естественно, представляет большие удобства для анализа переходных процессов.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|