
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Асинхронная машина. 13 страница
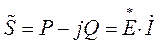
Совместив ось действительных с векторами э.д.с. 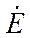 , имеем:
, имеем:

Таким образом, получаем 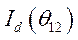 и
и 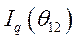
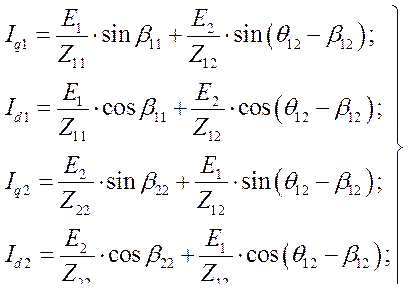 (454)
(454)
Во всех выражениях (452), (453) и (454) единственным «механическим» параметром является угол рассогласования роторов, 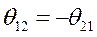 , параллельно работающих генераторов. Этот угол входит во все перечисленные выше мощности и токи и не зависит от «электрических» характеристик схемы замещения, а определяется исключительно мощностями первичных двигателей и законами управления этими мощностями.
, параллельно работающих генераторов. Этот угол входит во все перечисленные выше мощности и токи и не зависит от «электрических» характеристик схемы замещения, а определяется исключительно мощностями первичных двигателей и законами управления этими мощностями.
Полученные зависимости от угла  активных мощностей
активных мощностей  и
и 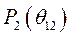 позволяет объяснить известные, но не очевидные факты. Почему после введения на параллельную работу генераторы устойчиво удерживаются в синхронизме? Почему короткое замыкание на сборных шинах или вблизи от них приводит к нарушению динамической устойчивости, которое проявляется выпадением из синхронизма работающих генераторов?
позволяет объяснить известные, но не очевидные факты. Почему после введения на параллельную работу генераторы устойчиво удерживаются в синхронизме? Почему короткое замыкание на сборных шинах или вблизи от них приводит к нарушению динамической устойчивости, которое проявляется выпадением из синхронизма работающих генераторов?
Поставленные вопросы справедливы и для синхронных двигателей.
Удержание генераторов в синхронизме.
В соответствии с общим выражением электромагнитной мощности синхронной машины.
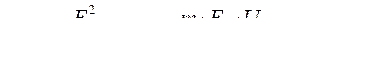 (455) где
(455) где  - число фаз:
- число фаз:
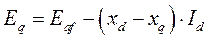 - э.д.с. за поперечной реактивностью;
- э.д.с. за поперечной реактивностью;
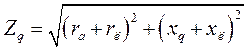 ;
;
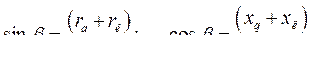
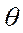 - угол сдвига по фазе между
- угол сдвига по фазе между  и
и 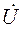 (угол нагрузки), в генераторном режиме вектор
(угол нагрузки), в генераторном режиме вектор  опережает по фазе комплекс
опережает по фазе комплекс 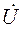 . То же относится к изображающим векторам на пространственной диаграмме. Возвратимся к режиму работы двух генераторов на общую нагрузку.
. То же относится к изображающим векторам на пространственной диаграмме. Возвратимся к режиму работы двух генераторов на общую нагрузку.
 Пусть генераторы имеют разные по модулю э.д.с.
Пусть генераторы имеют разные по модулю э.д.с. 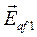 и
и 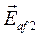 и несут неодинаковую нагрузку. Тогда, в общем случае, углы нагрузок
и несут неодинаковую нагрузку. Тогда, в общем случае, углы нагрузок 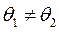 . Это отражено на векторной пространственной диаграмме, рис. 59.
. Это отражено на векторной пространственной диаграмме, рис. 59.
Уравнения динамического равновесия каждого из генераторов, запишутся в виде
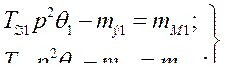 (456)
(456)
В о.е. электромагнитный момент генератора и его электромагнитная мощность равны по величине, но противоположны по знаку, то – есть:
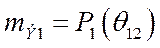 и
и 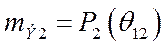
Это позволяет переписать уравнения (456), заменив моменты соответствующими мощностями
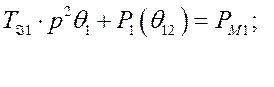 (457)
(457)
Как было показано выше, 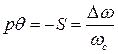 , где
, где 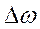 - положительное приращение скорости ротора генератора, а это значит, что
- положительное приращение скорости ротора генератора, а это значит, что
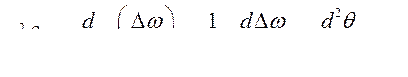 является ускорением ротора генератора.
является ускорением ротора генератора.
Разделим уравнения (457) относительно ускорений, рассматривая последние как функции угла рассогласования ротора 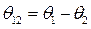
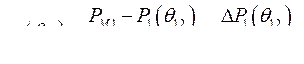 (458)
(458)
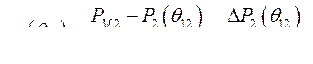 (459)
(459)
При неизменной подаче топлива или рабочего тела на первичные двигатели механические мощности, развиваемые ими, остаются неизменными, т.е.
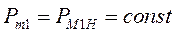 и
и 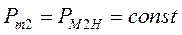
При отсутствии регулирования возбуждения
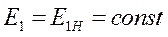 и
и 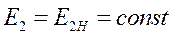
А также при неизменности нагрузки параметры 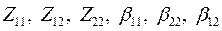 остаются неизменными.
остаются неизменными.
Отсюда следует, что избыточные мощности, 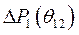 и
и 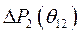 могут появиться исключительно при изменении угла
могут появиться исключительно при изменении угла 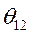 , поскольку в исходном установившемся режиме
, поскольку в исходном установившемся режиме
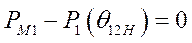 и
и 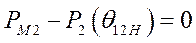 .
.
Флуктуации угла 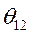 как результат флуктуации углов
как результат флуктуации углов  и
и 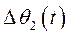 возникают неизбежно по разным причинам. Например, за счет колебания роторов синхронных машин относительно синхронной скорости, возникающих под воздействием внешних моментов вращения за счет неравномерности хода, либо за счет флуктуаций нагрузки. Если бы не существовало внутренних синхронизирующих моментов, регуляторы частоты первичных двигателей не смогли бы удержать генераторы в синхронизме.
возникают неизбежно по разным причинам. Например, за счет колебания роторов синхронных машин относительно синхронной скорости, возникающих под воздействием внешних моментов вращения за счет неравномерности хода, либо за счет флуктуаций нагрузки. Если бы не существовало внутренних синхронизирующих моментов, регуляторы частоты первичных двигателей не смогли бы удержать генераторы в синхронизме.
На векторной пространственной диаграмме, рис. 59, показано положение роторов генераторов в исходном установившемся режиме. Пусть по независимо какой причине угол рассогласования получит положительное приращение, 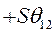 . Это приведет к изменению мощностей параллельно работающих генераторов. Согласно выражению (452),
. Это приведет к изменению мощностей параллельно работающих генераторов. Согласно выражению (452), 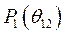 получит положительное приращение, а мощность
получит положительное приращение, а мощность 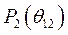 - отрицательное. При неизменности механических мощностей на валу первого генераторного агрегата появится отрицательный избыточный момент (мощность), а на валу второго – положительный,
- отрицательное. При неизменности механических мощностей на валу первого генераторного агрегата появится отрицательный избыточный момент (мощность), а на валу второго – положительный,
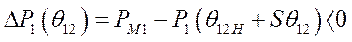
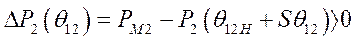
Это, в свою очередь, означает, что избыточные моменты начнут тормозить первый генератор и ускорять второй, выражения (458) и (459). При возвращении к исходному углу 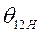 избыточные моменты исчезнут и ускорения станут равными нулю. В случае отрицательного приращения угла рассогласования
избыточные моменты исчезнут и ускорения станут равными нулю. В случае отрицательного приращения угла рассогласования 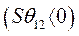 процесс возвращения к исходному значению
процесс возвращения к исходному значению 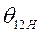 протекает аналогично, только избыточные мощности и ускорения меняют знаки.
протекает аналогично, только избыточные мощности и ускорения меняют знаки.
Таким образом, при всяком кратковременном возмущении, которое приводит к изменению угла 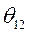 , в системе параллельно работающих синхронных машин возникают избыточные мощности и избыточные (синхронизирующие) моменты, направлены на восстановление исходного установившегося состоянии системы.
, в системе параллельно работающих синхронных машин возникают избыточные мощности и избыточные (синхронизирующие) моменты, направлены на восстановление исходного установившегося состоянии системы.
Опасность глубоких коротких замыканий вблизи
параллельно работающих генераторов и меры
повышения устойчивости.
При коротком замыкании на сборных шинах или вблизи от них, особенно при металлическом характере замыкания, сопротивление в точке к.з. близко к нулю. Схема замещения параллельной работы генераторов принимает вид, показанный на рис. 60.

Короткое замыкание шунтирует нагрузку, 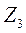 , то – есть в аварийном режиме
, то – есть в аварийном режиме 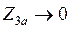 . А это значит, что
. А это значит, что
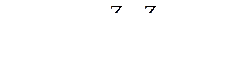
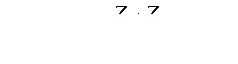
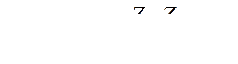
Электромагнитные мощности генераторов становятся равными

Другими словами, в электромагнитных мощностях отсутствует синхронизирующая составляющая
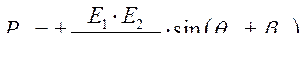 которая удерживала генераторы в синхронизме.
которая удерживала генераторы в синхронизме.
Ввиду того, что электромагнитные мощности в аварийном режиме не равны мощностям предыдущего установившегося, у генераторов появляются избыточные мощности и моменты, при этом вовсе не одинаковые. Это значит, что при отсутствии синхронизирующих мощностей и моментов угол рассогласования роторов 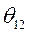 может неограниченно увеличиваться. Таким образом, возможна ситуация, что после ликвидации короткого замыкания или отключения поврежденного участка сети, угол рассогласования
может неограниченно увеличиваться. Таким образом, возможна ситуация, что после ликвидации короткого замыкания или отключения поврежденного участка сети, угол рассогласования 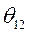 достигнет такой величины, что дальнейшая параллельная работа генераторов становится невозможной.
достигнет такой величины, что дальнейшая параллельная работа генераторов становится невозможной.
В реальности 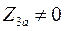 и
и 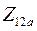 хоть и достигает значительных величин, тем не менее
хоть и достигает значительных величин, тем не менее 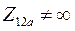 . Это значит, что хоть и небольшие, но синхронизирующие мощности и моменты сохраняются.
. Это значит, что хоть и небольшие, но синхронизирующие мощности и моменты сохраняются.
Существует два действенных метода сохранения устойчивости генераторов при коротких замыканиях и глубоких провалах напряжения на сборных шинах, а именно: отключение без выдержки времени поврежденного участка (токовая отсечка) и второй внешне парадоксальный способ – форсировка возбуждения. При этом увеличиваются э.д.с. 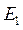 и
и 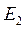 , а следовательно, увеличиваются синхронизирующие мощности и синхронизирующие моменты генераторов, что в свою очередь обеспечивает удержание генераторов в синхронизме.
, а следовательно, увеличиваются синхронизирующие мощности и синхронизирующие моменты генераторов, что в свою очередь обеспечивает удержание генераторов в синхронизме.
Уравнения элементов СЭС.
Уравнения многофазных сопротивлений в ортогональных
осях, вращающихся с произвольной скоростью.
В судовых электроэнергетических системах (СЭС) при анализе и моделировании необходимо учитывать параметры соединительных линий и уметь составлять уравнения статической нагрузки.
Эти элементы СЭС могут рассматриваться как многофазные сопротивления.
В свете изложенного вывод уравнений многофазных сопротивлений представляет несомненный интерес.
 Рассмотрим трехфазное сопротивление
Рассмотрим трехфазное сопротивление 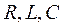 (рис. 61, где
(рис. 61, где 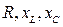 - активное, индуктивное и емкостное сопротивления фазы;
- активное, индуктивное и емкостное сопротивления фазы; 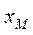 - сопротивление взаимной индукции).
- сопротивление взаимной индукции).
Для каждой фазы можно написать уравнения:
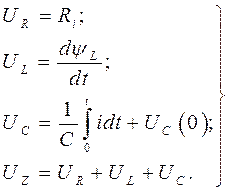 (460) или же, учитывая, что
(460) или же, учитывая, что  , предпоследнее уравнение системы (460) перепишем в виде
, предпоследнее уравнение системы (460) перепишем в виде
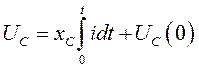 (461)
(461)
В уравнениях (460) и (461) обозначено:
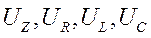 - мгновенные значения напряжений на зажимах сопротивлений суммарного, активного, индуктивного и емкостного;
- мгновенные значения напряжений на зажимах сопротивлений суммарного, активного, индуктивного и емкостного;
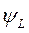 - потокосцепление фазы индуктивного сопротивления;
- потокосцепление фазы индуктивного сопротивления;
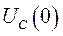 - напряжение на фазе емкости при
- напряжение на фазе емкости при 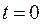 .
.
Построим две системы пространственных координатных осей: оси фаз 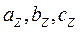 , сдвинутые относительно друг друга на угол
, сдвинутые относительно друг друга на угол
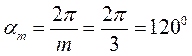 и ортогональные оси
и ортогональные оси 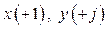 , вращающиеся относительно неподвижных осей
, вращающиеся относительно неподвижных осей 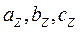 с некоторой угловой скоростью
с некоторой угловой скоростью 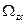 рис. 62.
рис. 62.
 Угол между
Угол между 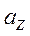 и
и 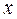

где  - угол при
- угол при 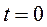 ;
;
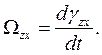
По осям соответствующих фаз откладываем мгновенные значения фазных падений напряжений на активных сопротивлениях. В результате получаем векторы 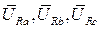 .
.
В осях  эти векторы выражаются как
эти векторы выражаются как
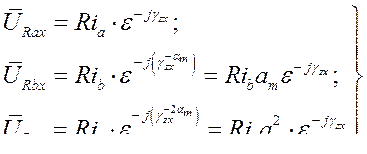 где
где 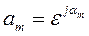 .
.
По определению изображающего вектора
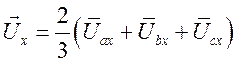 откуда и.в. падения напряжения на активном сопротивлении
откуда и.в. падения напряжения на активном сопротивлении
 (462) где
(462) где 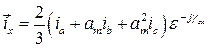 - и.в. трехфазной системы токов.
- и.в. трехфазной системы токов.
И.в. трехфазной системы падений напряжений на индуктивном сопротивлении
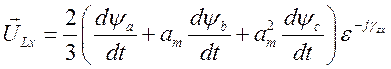 (463)
(463)
Учитывая то, что и.в. трехфазной системы потокосцеплений в осях  записывается как
записывается как
 его производная по времени будет иметь вид
его производная по времени будет иметь вид
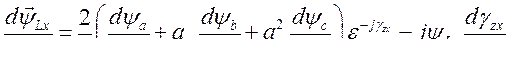 (464)
(464)
Из уравнений (463) и (464) находим
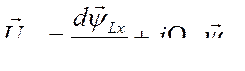 (465)
(465)
Полагая все сопротивления взаимной индукции равными друг другу, т.е. 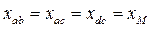 , для фазных потокосцеплений получим выражения
, для фазных потокосцеплений получим выражения
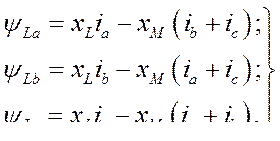 (466)
(466)
Знак 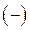 в правой части выражений (466) обязан тому факту, что при положительных токах а фазах н.с. любой фазы прямо противоположна н.с. двух других фаз.
в правой части выражений (466) обязан тому факту, что при положительных токах а фазах н.с. любой фазы прямо противоположна н.с. двух других фаз.
Вводя уравнения (466) в уравнение (465), для изображающего вектора напряжений на индуктивности 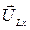 имеем
имеем
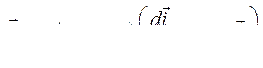 (467)
(467)
Уравнение (467) в операторной форме при нулевых начальных условиях примет вид
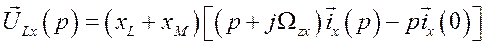 (468)
(468)
Спроектировав уравнение (468) на оси  , вращающиеся с произвольной скоростью, получим
, вращающиеся с произвольной скоростью, получим
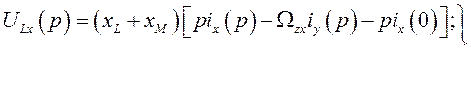 (469)
(469)
В уравнениях (468) и (469) 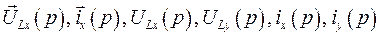 - изображения по Хевисайду соответствующих функций времени.
- изображения по Хевисайду соответствующих функций времени.
Наконец, найдем и.в. трехфазной системы падений напряжений на трехфазном конденсаторе.
По определению изображающего вектора
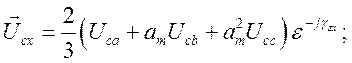 его производная по времени
его производная по времени
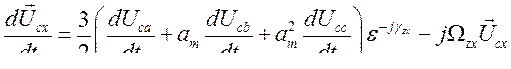 (470)
(470)
Производная по времени от падения напряжения на любой фазе емкости может быть получена из выражения (461):
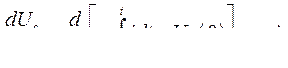 (471)
(471)
Уравнение (470) с учетом (471) примет вид
 (472)
(472)
Переходя к операторной форме, уравнение (472) представим выражение
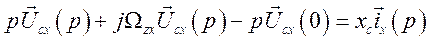 или
или
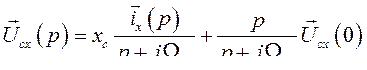 (473) где
(473) где
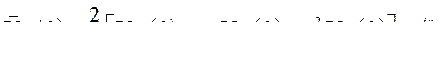
Поскольку для каждой фазы нагрузки справедливо равенство
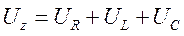 то для и.в. трехфазной системы падений напряжений на нагрузке можно записать
то для и.в. трехфазной системы падений напряжений на нагрузке можно записать
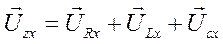 или в операторной форме
или в операторной форме
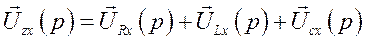 (474)
(474)
Подставим в выражение (474) значения и. в. 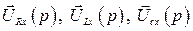 из (462), (468) и (473). Тогда
из (462), (468) и (473). Тогда
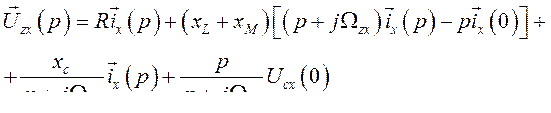 или
или
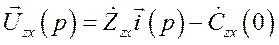 где
где
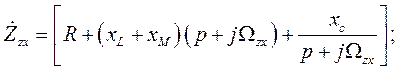
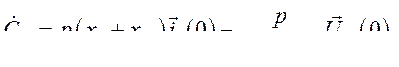
Представив напряжение 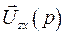 в виде суммы проекций на оси
в виде суммы проекций на оси  :
:
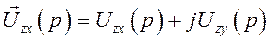 для соответствующих его проекций будет иметь
для соответствующих его проекций будет иметь
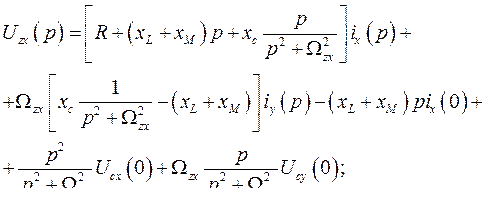
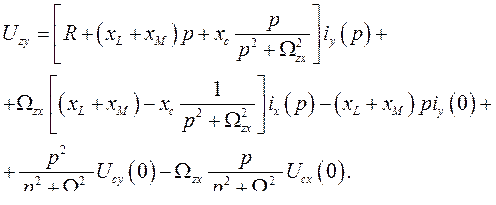
Уравнения элементов СЭС в
относительных единицах.
Как правило, расчеты и моделирование процессов в СЭС осуществляются по уравнениям, записанным в относительных единицах (о.е.). Использование о.е. имеет ряд достоинств: в частности, появляется возможность получить определенные безразмерные критерии, использовать номограммы в расчетах, а также более рельефно выделить особенности того или иного элемента СЭС.
Система базисных величин.
В данном пособии в качестве базисных принимаются следующие величины:
Основные:
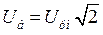 - амплитуда номинального фазного напряжения статорной обмотки;
- амплитуда номинального фазного напряжения статорной обмотки;
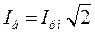 - амплитуда номинального фазного тока статорной обмотки;
- амплитуда номинального фазного тока статорной обмотки;
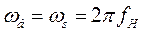 - синхронная угловая частота;
- синхронная угловая частота;
Производные:
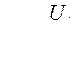 - потокосцепление;
- потокосцепление;
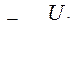 - сопротивление;
- сопротивление;
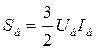 - полная (трехфазная) мощность;
- полная (трехфазная) мощность;
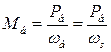 - вращающий момент, соответствующий активной мощности
- вращающий момент, соответствующий активной мощности 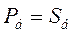 при синхронной (базисной) угловой частоте.
при синхронной (базисной) угловой частоте.
В качестве базисного тока в контуре, расположенном по продольной оси ротора, принимаем ток, который при холостом ходе машины дает базисное напряжение на зажимах фазной обмотки статора, т.е.
 - базисный ток обмотки возбуждения;
- базисный ток обмотки возбуждения;
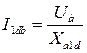 - базисный ток успокоительной обмотки по продольной оси ротора.
- базисный ток успокоительной обмотки по продольной оси ротора.
Базисный ток успокоительной обмотки по поперечной оси ротора определяется аналогично:
По базисным токам находим базисные напряжения, сопротивления и потокосцепления соответствующих контуров:
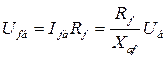 - базисное напряжение обмотки возбуждения;
- базисное напряжение обмотки возбуждения;
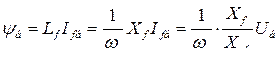 - базисное потокосцепление обмотки возбуждения;
- базисное потокосцепление обмотки возбуждения;
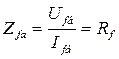 - базисное сопротивление обмотки возбуждения;
- базисное сопротивление обмотки возбуждения;
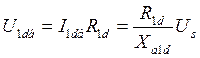 - базисное напряжение успокоительной обмотки по продольной оси ротора;
- базисное напряжение успокоительной обмотки по продольной оси ротора;
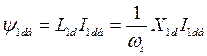 - базисное потокосцепление успокоительной обмотки по продольной оси ротора;
- базисное потокосцепление успокоительной обмотки по продольной оси ротора;
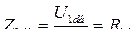 - базисное сопротивление успокоительной обмотки по продольной оси ротора;
- базисное сопротивление успокоительной обмотки по продольной оси ротора;
 - базисное напряжение успокоительной обмотки по поперечной оси ротора;
- базисное напряжение успокоительной обмотки по поперечной оси ротора;

 - базисное потокосцепление успокоительной обмотки по поперечной оси ротора;
- базисное потокосцепление успокоительной обмотки по поперечной оси ротора;
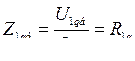 - базисное сопротивление успокоительной обмотки по поперечной оси ротора.
- базисное сопротивление успокоительной обмотки по поперечной оси ротора.
Уравнения синхронной машины в переменных 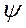 ,
,
записанные в о.е.
При записи уравнений синхронной машины в о.е. исходим из её уравнений, записанных в следующей форме:
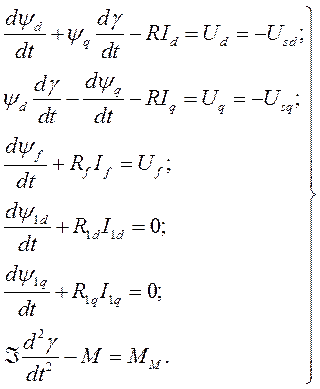 (475) где
(475) где 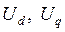 - проекции и.в. на оси d и q напряжений, генерируемых синхронной машиной;
- проекции и.в. на оси d и q напряжений, генерируемых синхронной машиной;
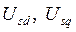 - проекции и.в. напряжений, приложенных к синхронной машине от сети, с которой она работает, на те же оси d и q;
- проекции и.в. напряжений, приложенных к синхронной машине от сети, с которой она работает, на те же оси d и q;
 - электромагнитный момент, развиваемый синхронной машиной.
- электромагнитный момент, развиваемый синхронной машиной.
Разделив все элементы первых двух уравнений системы (475) на 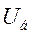 , получим:
, получим:
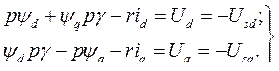 (746) где
(746) где 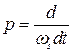 - оператор дифференцирования по синхронному времени.
- оператор дифференцирования по синхронному времени.
Элементы третьего уравнения системы (475) делим на 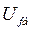 :
:
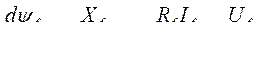 или
или
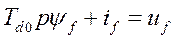 (477) где
(477) где 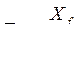 - постоянная времени цепи возбуждения при разомкнутой цепи статора (в синхронных секундах).
- постоянная времени цепи возбуждения при разомкнутой цепи статора (в синхронных секундах).
Элементы четвертого уравнения системы (475) делим на 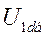 :
:
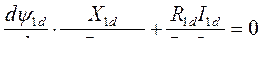 или
или
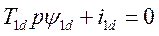 (478) где
(478) где 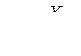 - постоянная времени успокоительного контура по продольной оси в синхронных секундах.
- постоянная времени успокоительного контура по продольной оси в синхронных секундах.
Разделив элементы пятого уравнения системы (475) на 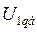 , получим аналогичное уравнение:
, получим аналогичное уравнение:
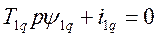 (479) где
(479) где 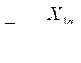 - постоянная времени (в синхронных секундах) успокоительного контура по поперечной оси.
- постоянная времени (в синхронных секундах) успокоительного контура по поперечной оси.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|