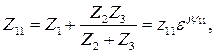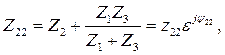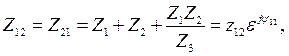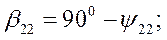- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Асинхронная машина. 15 страница
Расчет установок защиты синхронных генераторов из условия
сохранения динамической устойчивости судовой
электроэнергетической системы.
При решении данного вопроса будем пользоваться методом, принимающим неизменной э.д.с. за переходной реактивностью генератора. Это допущение можно обосновать тем известным фактом, что у синхронной машины без успокоительных контуров э.д.с. за переходной реактивностью 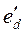 в о.е. равна потокосцеплению обмотки возбуждения:
в о.е. равна потокосцеплению обмотки возбуждения:
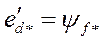 .
.
С другой стороны, потокосцепление обмотки возбуждения синхронной машины в динамических режимах изменяется достаточно медленно за счет вытеснения потока реакции якоря из обмоток ротора. Поэтому допущение
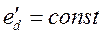
Соответствует истинному положению вещей в достаточно большом интервале времени от момента начала динамического режима.
Рассмотрим два синхронных генератора без успокоительных обмоток, работающих на общую нагрузку. Они описываются следующей системой уравнений:
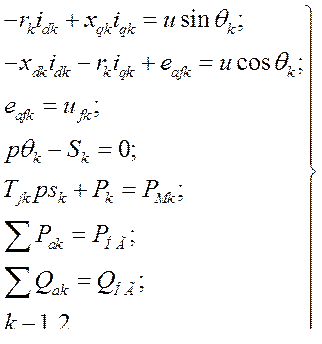
Введем в уравнения статорных обмоток вместо э.д.с 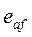 э.д.с.
э.д.с. 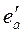 . По определению
. По определению
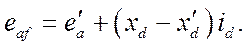
Таким образом
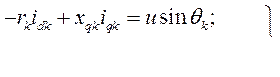
Другими словами, реальный генератор с э.д.с. 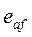 и реактивностью
и реактивностью 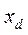 подменяем эквивалентным с э.д.с.
подменяем эквивалентным с э.д.с. 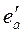 и реактивностью
и реактивностью 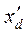 .
.
Угловая характеристика активной мощности эквивалентного генератора при 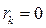 выражается уравнением
выражается уравнением

Ввиду того, что у судовых генераторов 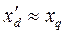 , вторую гармонику угловой характеристики можно опустить. Тем самым, вместо э.д.с.
, вторую гармонику угловой характеристики можно опустить. Тем самым, вместо э.д.с. 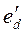 и угла
и угла 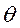 в расчет вводятся некоторые фиктивные величины
в расчет вводятся некоторые фиктивные величины 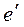 и
и 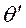 ; тогда
; тогда
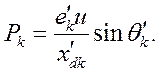
При вычислении относительного угла рассогласования принимают 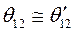 . При этом ошибка, обусловленная указанными допущениями, незначительна. Таким образом, исследуемые генераторы замещены во всех режимах (начальном, аварийном, а также послеаварийном)эквивалентными с одинаковыми реактивными по продольной и поперечной осям -
. При этом ошибка, обусловленная указанными допущениями, незначительна. Таким образом, исследуемые генераторы замещены во всех режимах (начальном, аварийном, а также послеаварийном)эквивалентными с одинаковыми реактивными по продольной и поперечной осям - 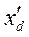 и э.д.с. за переходной реактивностью -
и э.д.с. за переходной реактивностью - 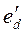 , неизменной в течении всего динамического режима.
, неизменной в течении всего динамического режима.
 Однолинейная схема замещения параллельной работы эквивалентных генераторов представлена на рис. 66
Однолинейная схема замещения параллельной работы эквивалентных генераторов представлена на рис. 66
Здесь
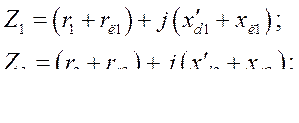
В результате анализа работы данной схемы можно записать угловые характеристики активных мощностей генераторов в виде:
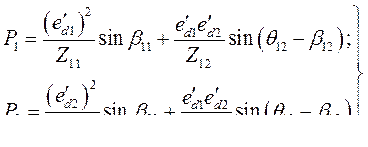
Где
|
|
| ||
|
|
| ||
|
|
| ||
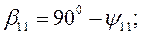
|
| 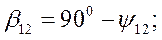
| |
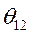 - угол рассогласования осей роторов генераторов
- угол рассогласования осей роторов генераторов 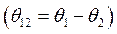 .
.
При анализе динамической устойчивости (ДУ) собственные и взаимные полные сопротивления должны быть вычислены для каждой из трех систем, соответствующих режимам: нормальному, аварийному и послеаварийному. При этом считаем, что э.д.с. 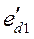 и
и 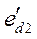 сохраняют одни и те же значения во всех трех схемах и определяются по условиям начального режима.
сохраняют одни и те же значения во всех трех схемах и определяются по условиям начального режима.
Зависимости электромагнитных мощностей 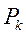 в функции угла
в функции угла 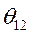 и уравнения механического равновесия генераторов дают возможность вычислить предельный угол
и уравнения механического равновесия генераторов дают возможность вычислить предельный угол 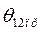 , соответствующий границе динамической устойчивости, с помощью преобразованного правила площадей. С этой целью, используя выражения для мощностей, отдаваемых генераторами, можно найти изменение избытков мощностей в функции
, соответствующий границе динамической устойчивости, с помощью преобразованного правила площадей. С этой целью, используя выражения для мощностей, отдаваемых генераторами, можно найти изменение избытков мощностей в функции 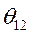 :
:
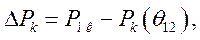 а затем построить в о.е. кривые изменения абсолютных ускорений
а затем построить в о.е. кривые изменения абсолютных ускорений
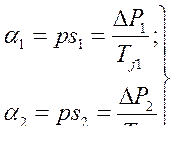
И относительного ускорения
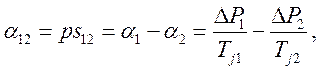 где
где  - символ дифференцирования по синхронному времени.
- символ дифференцирования по синхронному времени.
Относительное ускорение можно представить в виде
 (509) откуда
(509) откуда
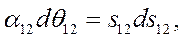 где
где  - относительное скольжение роторов генераторов.
- относительное скольжение роторов генераторов.
Интегрирование выражения (509) дает
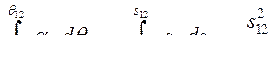 (510)
(510)
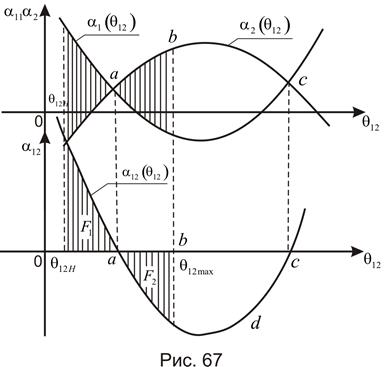
Зависимости абсолютных и относительных ускорений от угла 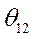 для аварийного режима представлены на рис. 67.
для аварийного режима представлены на рис. 67.
Левая часть выражения (510) равна площади, ограниченной кривой 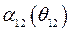 и осью
и осью 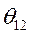 . Эта площадь пропорциональна квадрату относительной скорости машин. От
. Эта площадь пропорциональна квадрату относительной скорости машин. От 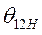 до точки
до точки 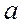 относительное ускорение положительно, за точкой
относительное ускорение положительно, за точкой 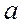 - отрицательно. Таким образом, максимальное значение относительного угла
- отрицательно. Таким образом, максимальное значение относительного угла 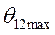 можно определить графически из условия равенства работ ускорения и торможения, что сводится к условию равенства площадей, ограниченной кривой
можно определить графически из условия равенства работ ускорения и торможения, что сводится к условию равенства площадей, ограниченной кривой 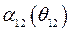 над осью
над осью 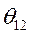 и под этой осью. Действительно, работа ускорения
и под этой осью. Действительно, работа ускорения
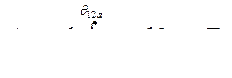 работа торможения
работа торможения
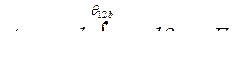
Максимальная площадь торможения
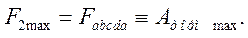
Если 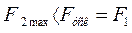 , система теряет устойчивость. Это явление имеет место при глубоких коротких замыканиях в системе. В самом деле, при к.з. на сборных шинах
, система теряет устойчивость. Это явление имеет место при глубоких коротких замыканиях в системе. В самом деле, при к.з. на сборных шинах 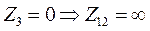 и поэтому
и поэтому 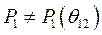 и
и 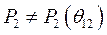 . Отсюда следует, что
. Отсюда следует, что 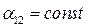 и работа по относительному ускорению не меняет знака. Однако при достаточно быстром отключении поврежденного участка можно достигнуть значительного запаса устойчивости.
и работа по относительному ускорению не меняет знака. Однако при достаточно быстром отключении поврежденного участка можно достигнуть значительного запаса устойчивости.
Для режима после отключения к.з. (послеаварийного режима), так же как и при к.з., можно построить кривую относительного ускорения 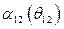 (рис. 68)
(рис. 68)
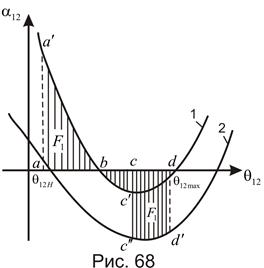
Сначала процесс изменения угла 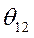 протекает по кривой 1 (характеристика аварийного режима). При отключении поврежденного участка в некоторой точке
протекает по кривой 1 (характеристика аварийного режима). При отключении поврежденного участка в некоторой точке 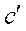 происходит переход на характеристику послеаварийного режима (кривая 2). Поэтому возможная площадь относительного торможения возрастает.
происходит переход на характеристику послеаварийного режима (кривая 2). Поэтому возможная площадь относительного торможения возрастает.
Предельный угол отключения к.з. определяется равенством площадей ускорения и торможения 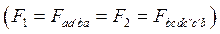 (рис. 69).
(рис. 69).
При расчетах ДУ СЭС, как правило, требуется знать не только предельный угол 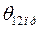 , но и предельное время отключения короткого замыкания
, но и предельное время отключения короткого замыкания 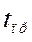 .
.
 При известном предельном угле
При известном предельном угле 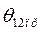 предельное время отключения к.з. находится из следующих соображений:
предельное время отключения к.з. находится из следующих соображений:

откуда
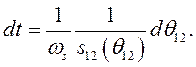 (511)
(511)
Проинтегрируем обе части уравнения (511). Изменению угла 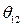 от
от 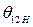 до
до 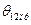 соответствует изменение времени от 0 до
соответствует изменение времени от 0 до 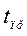 :
:
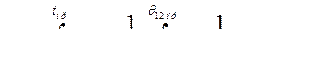 (512)
(512)
Относительно скольжение 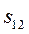 как функцию
как функцию 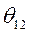 находим из выражения (510):
находим из выражения (510):
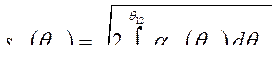 (513)
(513)
Подставив выражение (513) в (512), получаем предельное время 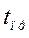 как функцию
как функцию 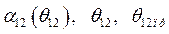 :
:
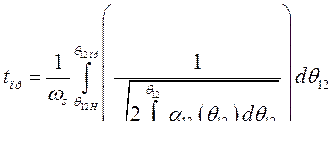 (514)
(514)
При наличии зависимости 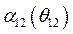 определение
определение 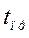 из (514) не представляет большой трудности. Задача проще всего решается методами численного интегрирования. Величины
из (514) не представляет большой трудности. Задача проще всего решается методами численного интегрирования. Величины 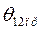 и
и 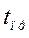 определяются в следующем порядке.
определяются в следующем порядке.
Исходные данные:
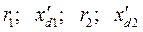 - сопротивления обмоток генераторов;
- сопротивления обмоток генераторов;
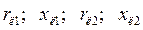 - сопротивления линий связи;
- сопротивления линий связи;
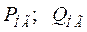 - активная и реактивная мощности на фазу нагрузки в доаварийном режиме;
- активная и реактивная мощности на фазу нагрузки в доаварийном режиме;
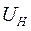 - напряжение на фазе нагрузки в доаварийном режиме;
- напряжение на фазе нагрузки в доаварийном режиме;
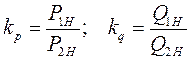 - отношения активных и реактивных мощностей, отдаваемых генераторами нагрузки.
- отношения активных и реактивных мощностей, отдаваемых генераторами нагрузки.
Кроме этого необходимо знать место и глубину к.з. на эквивалентной схеме (рис. 70).
Сопротивления фазы нагрузки:

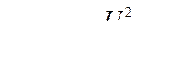
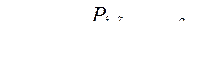

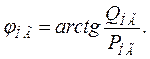
Для определения активных и реактивных токов генераторов используем выражения:
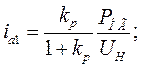
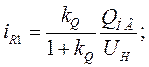

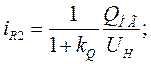
Э.д.с. за переходной реактивностью 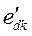 находим, воспользовавшись векторной диаграммой, изображенной на рис. 71.
находим, воспользовавшись векторной диаграммой, изображенной на рис. 71.
Здесь
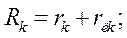
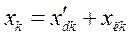
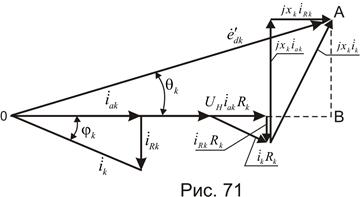
Откуда
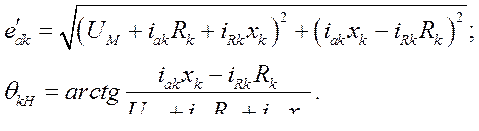
Электромагнитная мощность, развиваемая 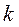 -м генератором в доаварийном режиме,
-м генератором в доаварийном режиме,
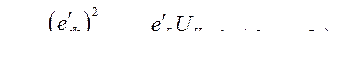 где
где
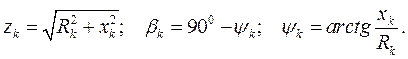
Угол рассогласования векторов э.д.с. генераторов в доаварийном режиме
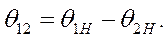
Не будет лишним напомнить, что в доаварийном режиме
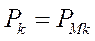
И в дальнейших расчетах 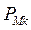 и
и 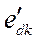 остаются неизменными.
остаются неизменными.
Затем определяем параметры аварийного и послеаварийного режимов:
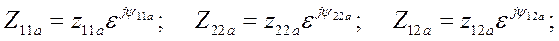
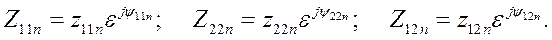
Строим характеристики 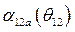 и
и 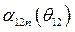 для аварийного и послеаварийного режимов (см. рис. 69)
для аварийного и послеаварийного режимов (см. рис. 69)
Далее, методами численного интегрирования находим зависимости
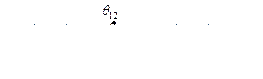
И
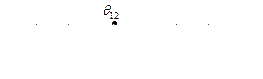
Причем 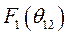 определяется путем интегрирования функции
определяется путем интегрирования функции 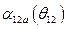 от
от 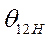 в сторону увеличения угла, а
в сторону увеличения угла, а 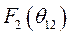 путем интегрирования функции
путем интегрирования функции 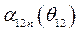 от
от 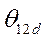 в сторону уменьшения угла
в сторону уменьшения угла 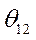 .
.
Предельный угол срабатывания защиты 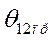 определяется из условия
определяется из условия
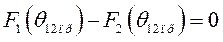
После определения 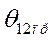 переходим к нахождению предельного времени срабатывания защиты
переходим к нахождению предельного времени срабатывания защиты 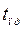 . Задача решается путем численного интегрирования выражения (514). При этом следует помнить, что процесс изменения угла
. Задача решается путем численного интегрирования выражения (514). При этом следует помнить, что процесс изменения угла 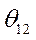 в промежутке от
в промежутке от 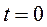 до
до 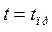 протекает по кривой, соответствующей аварийному режиму
протекает по кривой, соответствующей аварийному режиму 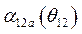 .
.
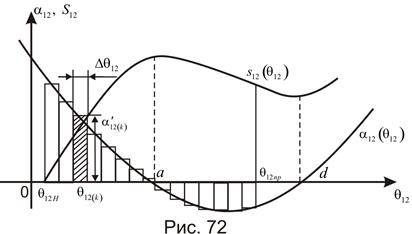
Разделив весь процесс изменения угла между роторами генераторов на достаточно малые интервалы 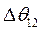 , расчет сводим в таблицу 3
, расчет сводим в таблицу 3
Алгоритм расчета иллюстрируется на рис. 72
Таблица 3.
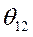
| 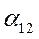
| 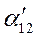
| 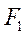
| 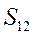
| 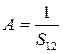
|
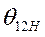
| 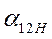
| ||||
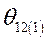
| 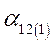
| 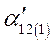
| 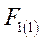
| 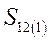
| 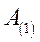
|
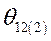
| 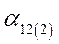
| 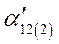
| 
| 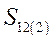
| 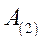
|
| 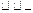
| 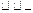
| 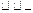
| 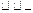
| 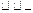
|
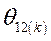
| 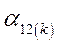
| 
| 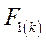
| 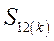
| 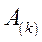
|
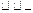
| 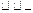
| 
| 
| 
| 
|
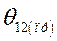
| 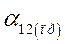
| 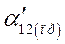
| 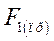
| 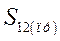
| 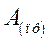
|
Расчетные формулы:
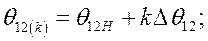
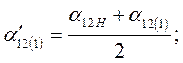
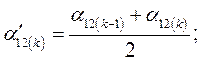
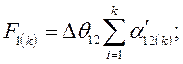
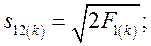
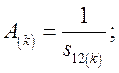
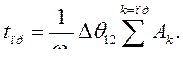
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|