Асинхронная машина. 7 страница

Тот факт, что функция Лагранжа содержит только и 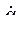, но не более высокие производные координат по времени, является выражением упомянутого выше факта, что состояние системы полностью определяется заданием координат и скоростей как функцией времени и начального состояния. Объяснением этого на первый взгляд неубедительного утверждения может служить следующее. Физические законы, являющиеся фундаментом электромеханики, не содержат выше второй производной от переменных (координат), а это значит, что при решении дифференциального уравнения для конкретного частного случая необходимо знать начальную координату и начальное значение её первой производной. Действительно, если

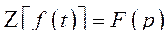То .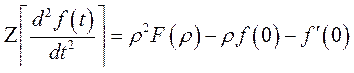

Перейдем к выводу дифференциальных уравнений, решающих задачу об определении минимума интеграла (221). Для упрощения записи формул предположим сначала, что система обладает всего одной степенью свободы, так что должна быть определена всего одна функция .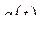

Пусть 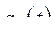- вещественная функция, делающая функционал

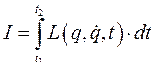экстремальным.

Выберем некоторую непрерывную, дифференцируемую функцию 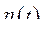(произвольно), но она должна в точках 1 и 2 принимать нулевые значения, т.е. 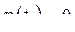и .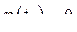

Тогда функцию 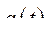можно представить в виде

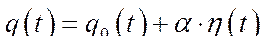(223)

где 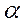- некоторая постоянная (тоже в общем случае выбранная произвольно) и функция 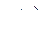из выражения (223) будет удовлетворять граничным условиям

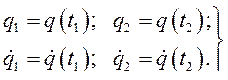(224)

Запишем функционал 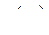, полученный в результате подстановки

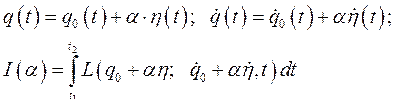(225)

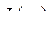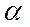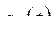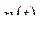Функционал является только функцией параметра , т.к. и определены заранее и к тому же функционал 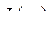имеет экстремум при 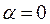, потому, что 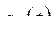выбрана именно из этого условия.

Однако, с позиций математики, это возможно при условии, что

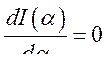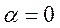при (226)

Следовательно, уравнение (226) является условием существования экстремума. Последнее можно теперь применить к уравнению (225). При этом так-как 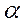- величина, не зависящая от времени, (не зависящий от времени параметр), процесс дифференцирования можно осуществить под знаком интеграла

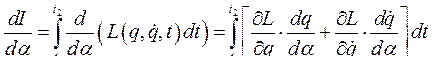(227)

В свою очередь

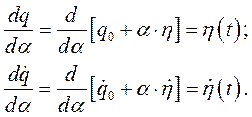
Таким образом,

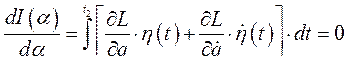(228)

Вариации, не зависящие от времени (S – вариации).

Рассмотрим случай, когда времена 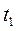и 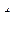граничных точек фиксированы; 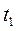и - заданы и остаются неизменными. Подынтегральная функция 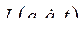- является определенной функцией переменных , и 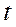, например:

Определим вариацию функции L в зависимости от вариаци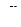й и 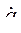; время при этом не варьируется.

Функция 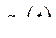была определена как вещественная функция, дающая экстремум функционалу

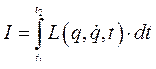
А некоторая другая функция на конечном промежутке определена уравнением (223)

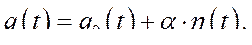
Теперь определим вариацию 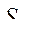как вариацию функции 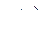из вещественной функции 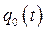. Это дает

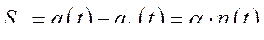(229)

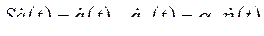(230)

Следующий шаг – нахождение вариации функции переменных и 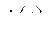, например вариации .

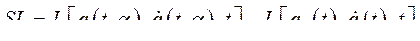(231)

Раскладывая первый член в уравнении (231) в ряд Тейлора по 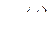и и ограничивалась только первыми членами (величинами первого порядка малости), находим искомую вариацию.

Примечание. Ряд Тейлора функции 2-х переменных

Это позволяет записать

(232)

Таким образом, принимая во внимание (232), имеем:

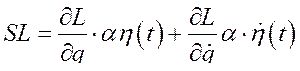(233)

или

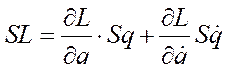(234)

Заметим, что выражение (234) для вариации 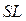функции L подобно выражению полного дифференциала от функции 2-х переменных.

Вернемся к условию существования экстремума функционала I, выражению (228).

Мы видим, что подынтегральная функция в выражении (228) равна выражению (233) деленному на . Поэтому, умножив (228) на получим

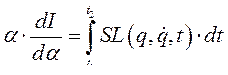(235)

В виду того, что , а условие существования экстремума записывается в виде

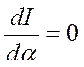
Его можно записывать в виде 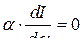или

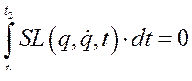(236)

Благодаря тому, что вариация не зависит от времени, её можно вынести за знак интеграла

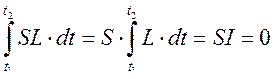(237)

Выражение - еще одно условие существования экстремума функционала I.

Уравнение Эйлера – Лагранжа.

Пусть дан функционал 2N переменных 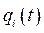и и t где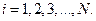

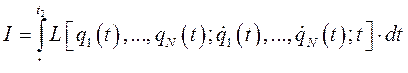(238)

Одним из условий существования экстремума данного функционала на конечном промежутке является требование, чтобы на границах данного промежутка 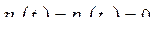или

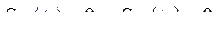при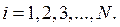

Так как вариация S по определению является независимой от времени t, её можно внести под знак интегрирования по времени/

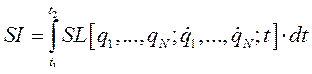(239)

Раскрывая выражение SL в уравнении (239), получим

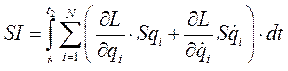(240)

С целью упрощения выражения (240) проинтегрируем по частям вотрое слагаемое под знаком 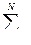в рассматриваемом интеграле

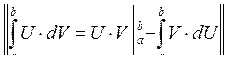
При этом поскольку вариация S не зависит от времени t, то

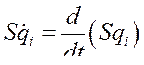(241)

Таким образом,

В свою очередь

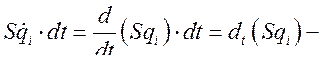(242)

Дифференциал по времени от S вариации 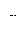координаты U

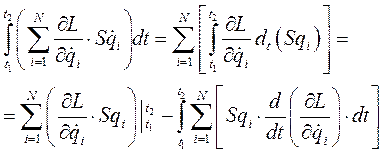(243)

Так как стремится к нулю на границах интервала интегрирования 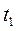и , т.е. и 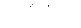, то первое слагаемое уравнения (243), где выступает сомножителем, равно нулю. Подстановка (243) в (240) дает

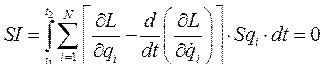(244)

Из последнего выражения легко вывести условие существования экстремума функционала I, которое выливается в уравнения Эйлера – Лагранжа.

Условия существования экстремума функционала I.

Из уравнения (244) становятся ясными условия, которым должна удовлетворять функция 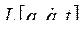, чтобы функционал I имел экстремум.

1. Во – первых, экстремум 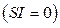должен сохраняться независимо от вариации любой координаты .

2. Кроме того, если N координат 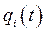независимы, т.е. нет уравнений связи, существующих между некоторыми из N координат , то единственный способ удовлетворить условие (244) – это приравнять к нулю сомножитель, стоящий в квадратных скобках под знаком суммы и интеграла для каждого значения 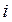. Тогда условие существования экстремума запишется в виде уравнения Эйлера – Лагранжа

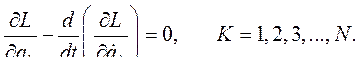(245)

Принцип Гамильтона (формулировка).

Действительная динамическая траектория системы, описываемой силовой функцией 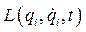, определяется путем нахождения экстремума функции I

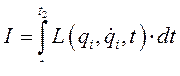
решением уравнений Эйлера – Лагранжа.

Силовые функции зависят исключительно от состояния системы в рассматриваемый момент времени (например, её энергия), а не от её (системы) предыстории.

Если функция Лагранжа данной электромеханической системы известна, то уравнения (245) устанавливают связь между ускорениями, скоростями и координатами, т.е. представляют собой уравнения движения системы. С математической точки зрения уравнения (245) составляют систему из N уравнений второго порядка для N неизвестных . Общее решение такой системы содержит 2N произвольных постоянных. Для их определения необходимо знание начальных условий, характеризующих состояние системы в некоторый заданный момент времени, например, знание начальных значений всех координат и скоростей.

Необходимо сделать ещё следующее общее замечание.

Рассмотрим две функции и , отличающиеся друг от друга на полную производную по времени от какой либо функции координат и времени :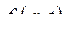

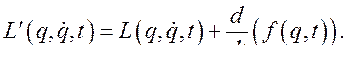
Вычисленные с помощью этих двух функций функционалы действия (244) связаны соотношением

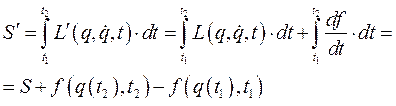
то – есть отличаются друг от друга дополнительным членом, исчезающим при варьировании действия. Действительно, вариации переменных, определяющих 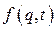в моменты времен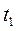и и равны нулю,

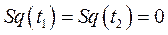и ,

следовательно,

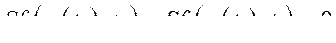
Таким образом, функция Лагранжа определена лишь с точностью до прибавления к ней полной производной от произвольной функции координат и времени. Это же значит, если в выражении функции Лагранжа присутствует полная производная по времени некоторой функции текущих координат и времени, эта производная может быть отброшена.

Уравнения элементов электроэнергетической системы

в вариациях. Линеаризованные уравнения системы.

При исследовании статической устойчивости и при решении ряда задач управления энергетической системой достаточно ограничится линеаризованными уравнениями её элементов. Эти линеаризованные уравнения или уравнения в вариациях можно получить из уравнений электрического и механического состояний либо при помощи ряда Тейлора, либо используя правила вариационного исчисления.

Напомним правила варьирования отдельных членов уравнений:

1) вариация функции находится по тем же правилам, что и её дифференциал;

2) значения функций, перед которыми отсутствует символ вариации, относят к первой неварьированной системе, т.е. снабжают индексом «Н»;

3) знаки вариации S и дифференцирования «р», относящиеся к одной и той же функции, могут быть переставляемы, то – есть порядок их не имеет значения.

Проиллюстрируем эти правила примерами:

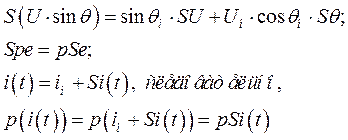
1. Уравнения синхронной машины в относительных единицах, записанные в вариациях.

Применим перечисленные выше правила варьирования к уравнениям системы

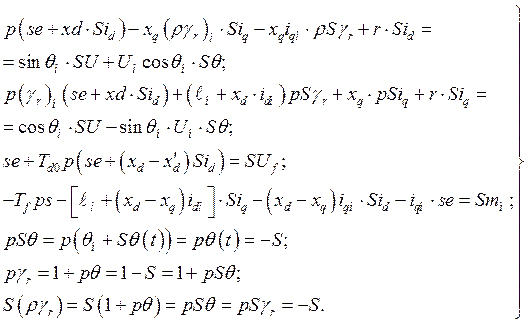
Линеаризованные уравнения асинхронной машины записанные в относительных единицах.

Применив правила варьирования к переменным, входящим в уравнения асинхронной машины, приведенным к безразмерному виду, получим

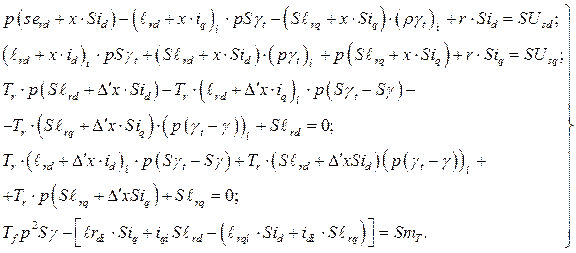
Статическая устойчивость.

Анализ корней характеристического уравнения системы, описываемой дифференциальными уравнениями, позволяет определить условия сохранения или нарушения статической устойчивости. Решение задачи рационального проектирования электроэнергетической системы или её элементов опирается на критерии статической устойчивости, найденные в общем виде. Получить эти критерии в общем виде удается для систем, порядок которых не превышает пяти. Объяснение этому достаточно просто: в настоящее время отсутствуют методы аналитического решения алгебраических уравнений с порядком выше пятого, а следовательно, невозможно в аналитической форме сформулировать соответствующие критерии.

Условия сохранения устойчивости работы синхронного генератора определим с помощью уравнений электрического и механического состояния в относительных единицах и вариациях

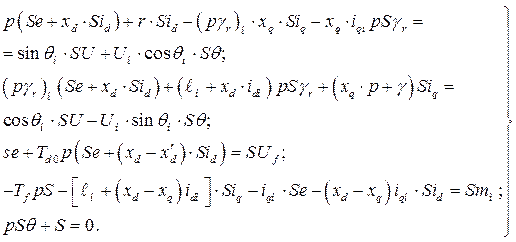(246)

Система (246) записана для генератора без учета влияния успокоительных контуров и может трансформироваться в зависимости от условий работы или принимаемых допущений.

При анализе устойчивости начнем с наиболее простой задачи с последующим её усложнением.

1. Устойчивость при учете исключительно механических переходных процессов (устойчивость по «сползанию ротора»)

При анализе данного режима принимаем следующие условия: напряжение в сети неизменно 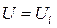, следовательно 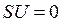; напряжение на обмотке возбуждения постоянно , следовательно 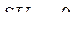; момент на валу первичного двигателя остается постоянным 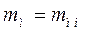, т.е. . Отличим связь между скоростью вращения ротора, его скольжением углом 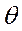, их производными и вариациями

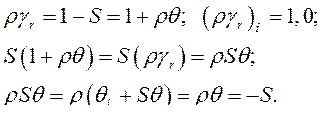
Пренебрегаем переходными электрическими колебаниями в цепях статора и ротора по сравнению с механическими колебаниями ротора. Другими словами, считаем, что по сравнению со временем изменения механической координаты 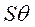электрические координаты 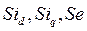устанавливаются мгновенно. С позиций математики это означает, что в первых трех уравнениях системы (246) операторы дифференцирования при этих переменных обращаются в ноль, . Более того, из уравнения цепи обмотки возбуждения в этом случае следует, что 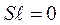. Кроме того, поскольку колебания достаточно малы, скольжение ротора практически не влияет на падение напряжений. Поэтому все члены уравнений умножены на скольжение в уравнениях электрического равновесия принимаем равным нулю. Простоты ради рассматриваем неявнополюсную машину, 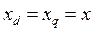. Окончательно система уравнений (246) сведется к виду:

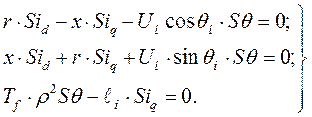(247)

В системе уравнений (247) 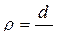- оператор дифференцирования по синхронному времени. Используя первые два уравнения, находим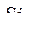

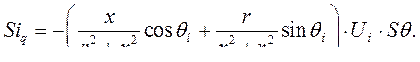
Обозначим , тогда

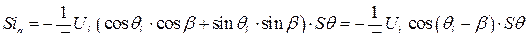(248)

Подставим 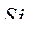, выражение (248) в третье уравнение системы (247)

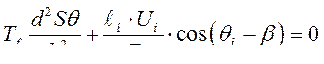(249)

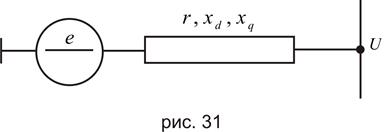
Мощность электромагнитная любого синхронного генератора может быть найдена с помощью выражения

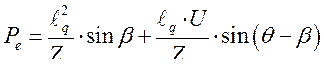(250)

Здесь 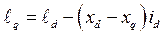- э.д.с. за поперечной реактивностью синхронного генератора или э.д.с эквивалентного генератора; в рассма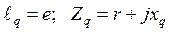триваемом случае , . В рассматриваемом случае

Производная от электромагнитной мощности по углу 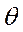равна

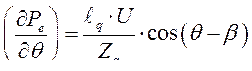(251)

и уравнение (251) приводится к виду

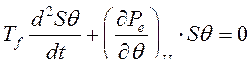(252)

Решение данного уравнения ищем, используя операторный метод. Запишем уравнение (252) в операторной форме по Лапласу.

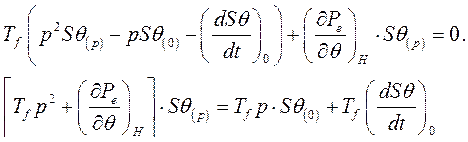
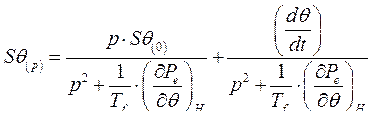(253)

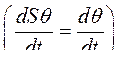
Обозначим

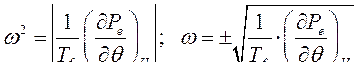
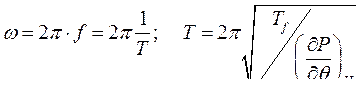
Инерционная постоянная времени 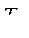всегда положительна 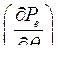- меняет знак в зависимости от режима, как это видно на рис. 32

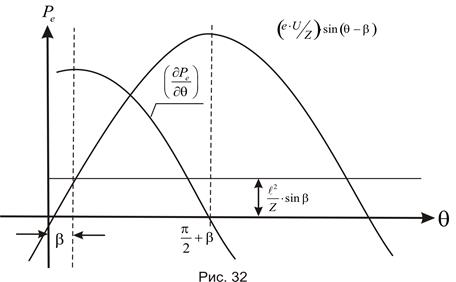
Поэтому выражение (253) в случае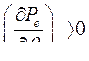

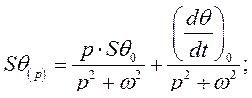(254)

а при 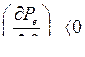соответственно

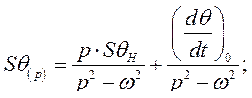(255)

Рассмотрим оба случая. При 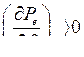обратное преобразование Лапласа выражения (255) дает

(256)

где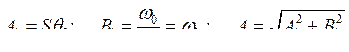

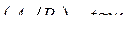
Согласно выражению (256) ротор совершает незатухающие колебания с постоянной частотой и амплитудой. Период колебаний T является функцией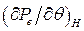

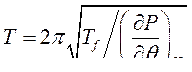(257)

при увеличении нагрузки от нуля до максимальной уменьшается, а период T растет.

В реальных режимах в синхронной машине имеют место потери в магнитопроводе, успокоительных короткозамкнутых контурах и на трение, которые в исходной системе уравнений не учтены. Благодаря наличию этих потерь, колебания ротора будут иметь затухающий характер.

Второй случай. Производная от электромагнитной мощности по углу нагрузки отрицательна, 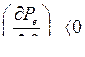. Обратное преобразование Лапласа выражения (257) дает 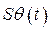в виде:

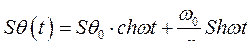(258)

В свою очередь

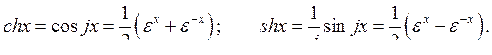
Это дает

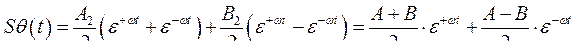
При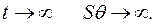

Другими словами, генератор выпадает из синхронизма, режим неустойчивый. Таким образом, критерием устойчивости по «сползанию ротора» является требование

(259)

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒