
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Асинхронная машина. 5 страница
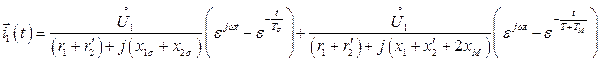 (161)
(161)
Здесь 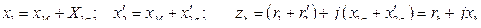 -сопротивление
-сопротивление
короткого замыкания.
Обозначим 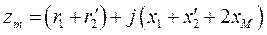
Это позволяет записать
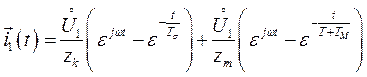 (162)
(162)
Другими словами, в момент подключения АМ под напряжение её можно рассматривать как подключение двух активно-индуктивных контуров
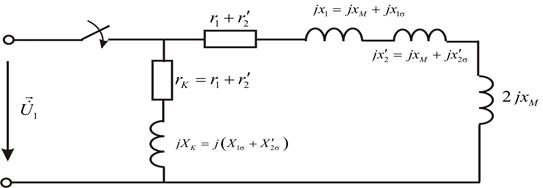
При этом у первого контура достаточно малая индуктивность, определяемая только потоками рассеяния, а у второго, индуктивность достаточно велика. Принимая во внимание, что
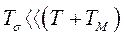 , а
, а 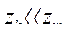
можно считать, что нарастание тока в обмотках генератора и провал напряжения определяются исключительно контуром 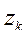
Из формул (161) и (162) следует, что в установившемся режиме
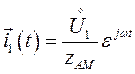 где
где 
Сопротивление 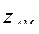 соответствует известной Т-образной схеме замещения асинхронной машины при неподвижном роторе.
соответствует известной Т-образной схеме замещения асинхронной машины при неподвижном роторе.
Электромагнитные моменты электрических машин.
Обобщенная сила и обобщенная координата.
 При определении электромагнитных моментов эл. машин воспользуемся известным в классической механике принципов возможных перемещений (он же принцип виртуальной работы). Этот принцип вытекает из общефизического закона сохранения энергии. При этом используют понятия обобщенных координат. Из всего разнообразия обобщенных координат нас интересуют, в первую очередь, обобщенная сила и обобщенная координата. Под ними понимают пару независимых физических характеристик любого процесса при условии, что их произведение имеет размерность работы (энергии). Рассмотрим примеры, рис. 22. Движение физического тела по траектории под действием силы. При прохождении отрезка dx сила
При определении электромагнитных моментов эл. машин воспользуемся известным в классической механике принципов возможных перемещений (он же принцип виртуальной работы). Этот принцип вытекает из общефизического закона сохранения энергии. При этом используют понятия обобщенных координат. Из всего разнообразия обобщенных координат нас интересуют, в первую очередь, обобщенная сила и обобщенная координата. Под ними понимают пару независимых физических характеристик любого процесса при условии, что их произведение имеет размерность работы (энергии). Рассмотрим примеры, рис. 22. Движение физического тела по траектории под действием силы. При прохождении отрезка dx сила 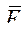 совершит элементарную работу
совершит элементарную работу 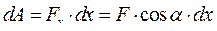 , следовательно, в рассматриваемом случае F – обобщенная сила, линейная координата
, следовательно, в рассматриваемом случае F – обобщенная сила, линейная координата 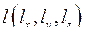 - линейная координата;
- линейная координата;
dx – её дифференциал в направлении перемещения в рассматриваемый момент.
Второй случай.
Под действием момента тело вращается. Элементарная работа при этом 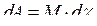 . Следовательно, под обобщенной силой в данном случае следует понимать момент, М, а под обобщенной координатой угол поворота,
. Следовательно, под обобщенной силой в данном случае следует понимать момент, М, а под обобщенной координатой угол поворота, 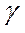 . Третий случай. Движение поршня под действием давления в цилиндре. Пусть мы в качестве обобщенной силы выбрали давление,
. Третий случай. Движение поршня под действием давления в цилиндре. Пусть мы в качестве обобщенной силы выбрали давление, 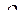 , в цилиндре. Элементарная работа по перемещению поршня запишется
, в цилиндре. Элементарная работа по перемещению поршня запишется 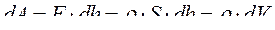 .
.
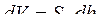 - приращение объема под поршнем. Следовательно, если в данном примере в качестве обобщенной силы принято давление,
- приращение объема под поршнем. Следовательно, если в данном примере в качестве обобщенной силы принято давление, 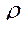 , то в качестве обобщенной координаты мы должны принять объем, V. В случае электрического контура элементарная энергия, поступающая на вход
, то в качестве обобщенной координаты мы должны принять объем, V. В случае электрического контура элементарная энергия, поступающая на вход
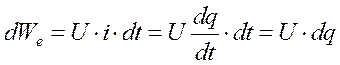 .
.
Следовательно, если в качестве обобщенной силы принять напряжение на входе контура, то в качестве обобщенной координаты мы обязаны рассматривать электрический заряд, поступающий в контур.
Электромагнитная цепь. Изменение энергии магнитного поля можно представить в виде
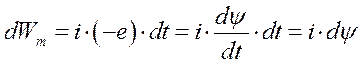
то-есть, если в качестве обобщенной силы принять ток, i, то в качестве обобщенной координаты мы должны принять изменяющееся потокосцепление электромагнитной цепи.
Энергия и коэнергия магнитного поля.
В электромагнитных системах наряду с энергией магнитного поля, определяемой как
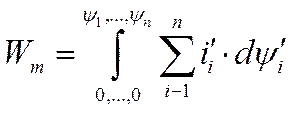 (163)
(163)
где 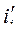 и
и 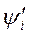 - текущие координаты тока и потокосцепления i-того контура, вводят понятие коэнергии магнитного поля, определяемой выражением
- текущие координаты тока и потокосцепления i-того контура, вводят понятие коэнергии магнитного поля, определяемой выражением
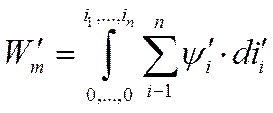 (164)
(164)
При определении энергии магнитного поля, Wm, в качестве независимой координаты принимается потокосцепление, 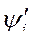 , а при определении коэнергии
, а при определении коэнергии  , в качестве независимой координаты принимают ток контура,
, в качестве независимой координаты принимают ток контура, 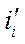 , по которому и производят интегрирование.
, по которому и производят интегрирование.
Если 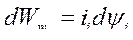 , то
, то 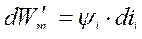 .
.
 Различие между энергией магнитного поля и его коэнергией легко показать на примере одной электромагнитной цепи. Пусть нам известна её характеристика
Различие между энергией магнитного поля и его коэнергией легко показать на примере одной электромагнитной цепи. Пусть нам известна её характеристика 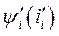 , рис. 23. При изменении потокосцепления от 0 до
, рис. 23. При изменении потокосцепления от 0 до 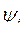 и тока от 0 до
и тока от 0 до 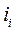 (до точки I на кривой) заштрихованная часть поля кривой в принятом масштабе равна энергии магнитного поля,
(до точки I на кривой) заштрихованная часть поля кривой в принятом масштабе равна энергии магнитного поля, 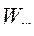 , а часть плоскости под кривой, ограниченная кривой
, а часть плоскости под кривой, ограниченная кривой  , осью абсцисс и ординатой
, осью абсцисс и ординатой 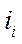 , в принятом масштабе равна коэнергии магнитного поля
, в принятом масштабе равна коэнергии магнитного поля 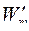 . При изменении параметров контура от точки 1 до точки 2 изменяется и энергия магнитного поля и его коэнергия, но их приращения в общем случае различны
. При изменении параметров контура от точки 1 до точки 2 изменяется и энергия магнитного поля и его коэнергия, но их приращения в общем случае различны
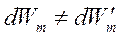 . (165)
. (165)
Последнее легко доказывается графически , см. рис. 23 и 24.
Возьмем достаточно малое расстояние между точками 1 и 2, соединим их линией и продолжим последнюю до пересечения с осью абсцисс 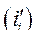 в точке (а, А). Построим два прямоугольника abcd и ABCD с общей диагональю AC, ac. Диагональ AC делит прямоугольник abcd на два равновеликих треугольника
в точке (а, А). Построим два прямоугольника abcd и ABCD с общей диагональю AC, ac. Диагональ AC делит прямоугольник abcd на два равновеликих треугольника 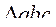 и
и 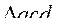 , аналогично диагональ AC делит прямоугольник ABCD на два равновеликих треугольника
, аналогично диагональ AC делит прямоугольник ABCD на два равновеликих треугольника 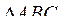 и
и 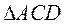 . Следовательно площадь трапеции bBCc равна площади трапеции CcdD
. Следовательно площадь трапеции bBCc равна площади трапеции CcdD
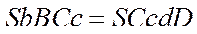 ,
,
но 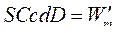 , а
, а 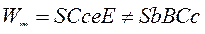 .
.
Несмотря на различие между 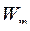 и
и 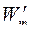 их сумма всегда равна произведению конечных координат, то-есть
их сумма всегда равна произведению конечных координат, то-есть
 (166)
(166)
Если зависимость между 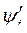 и
и 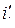 линейна
линейна
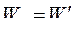
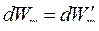 или
или 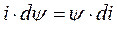 ,
,
а следовательно,
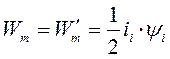 .
.
Для системы электромагнитных цепей имеем
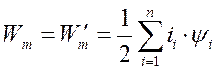 (167)
(167)
Принцип возможных перемещений в электромагнитной
системе.
Рассмотрим электромеханическую систему, рис. 25, у которой имеются механические входы, через которые подаются механические воздействия и электрические входы, через которые подаются электрические воздействия. Это приводит к тому, что у системы изменяются как механические, так и электромагнитные координаты.
Энергия, поступающая от некоторого К-го механического источника,

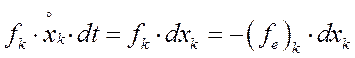
Здесь 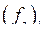 - сила реакции системы по К-той координате.
- сила реакции системы по К-той координате.
Энергия, поступающая от электрических источников
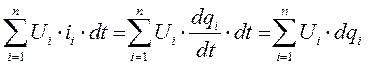 .
.
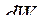 - изменение запасной энергии в системе.
- изменение запасной энергии в системе.
На основании закона сохранения энергии запишем
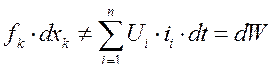 или
или
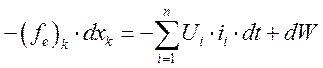 (168)
(168)
Если все диссипативные (рассеивающие энергию) элементы вынести во внешние цепи, система становится консервативной. В ней
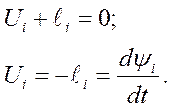
Это в свою очередь дает
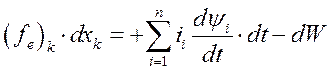 (169)
(169)
Откуда сила реакции системы по К – той координате
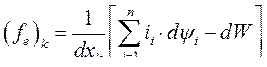 (170)
(170)
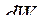 - полное приращение общей энергии системы. Нас интересует преобразование энергии магнитного поля в механическую и наоборот. С этой целью, рассмотрим систему контуров (обмоток), обтекаемых электрическим током. Единственно важным электромагнитным полем связи между различными элементами системы будет для квазистатического состояния (низкой скорости механических перемещений) магнитное поле.
- полное приращение общей энергии системы. Нас интересует преобразование энергии магнитного поля в механическую и наоборот. С этой целью, рассмотрим систему контуров (обмоток), обтекаемых электрическим током. Единственно важным электромагнитным полем связи между различными элементами системы будет для квазистатического состояния (низкой скорости механических перемещений) магнитное поле.
Подводимая электрическая энергия плюс подводимая механическая энергия системы будут определять изменение энергии магнитного поля, а именно:
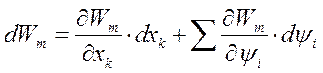 (171)
(171)
Выражение (171) требует некоторых пояснений.
Рассмотрим некоторую электромеханическую систему, состоящую из n – контуров, положение которых характеризуется m – механическими координатами. Энергия магнитного поля этой системы, на основании выражения (163) можно записать в виде
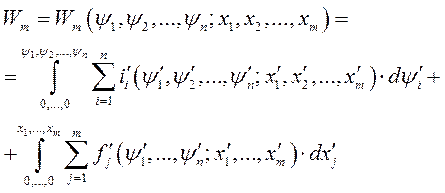 (172)
(172)
Здесь 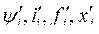 - текущие координаты.
- текущие координаты.
Выражение (172) отражает тот непреложный факт, что энергия магнитного поля электромеханической системы формируется за счет энергии, поступающей как от электрических источников, так и за счет энергии механических источников. При этом в общем случае изменяются как электрические, так и механические координаты.
У любой системы данного характера, для которой 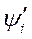 - однозначная функция от
- однозначная функция от 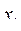 и
и 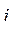 полная запасенная энергия магнитного поля
полная запасенная энергия магнитного поля 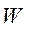 определяется единственно параметрами
определяется единственно параметрами 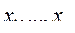 и
и 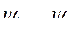 и зависит исключительно от конечных значений этих параметров. То-есть полная запасенная энергия магнитного поля является силовой функцией, то-есть не зависит от того каким образом система была приведена в заданное состояние. Например, поддерживая все потокосцепления равными нулю, соберем систему механически, а затем, оставляя механические координаты неизменными, установим потокосцепления. Для заданных значений и координат и потокосцеплений энергия запасенная в магнитном поле, будет подведена от электрических источников и её выражение будет иметь вид
и зависит исключительно от конечных значений этих параметров. То-есть полная запасенная энергия магнитного поля является силовой функцией, то-есть не зависит от того каким образом система была приведена в заданное состояние. Например, поддерживая все потокосцепления равными нулю, соберем систему механически, а затем, оставляя механические координаты неизменными, установим потокосцепления. Для заданных значений и координат и потокосцеплений энергия запасенная в магнитном поле, будет подведена от электрических источников и её выражение будет иметь вид
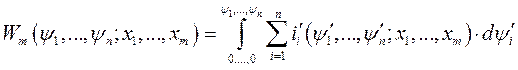 (173)
(173)
Здесь же уместно отметить: при неизменных механических координатах связь между токами контуров и их потокосцеплениями однозначна. Поэтому какую переменную 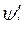 или
или 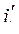 считать независимой, а какую её функцией, т.е.
считать независимой, а какую её функцией, т.е.
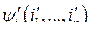 или
или 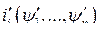 не принципиально. Поэтому в электромеханике в качестве независимых координат рассматривают либо пару переменных
не принципиально. Поэтому в электромеханике в качестве независимых координат рассматривают либо пару переменных 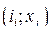 , либо
, либо 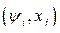 . В рассматриваемом случае в качестве независимых координат приняты потокосцепления
. В рассматриваемом случае в качестве независимых координат приняты потокосцепления 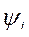 и механические координаты
и механические координаты 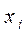 .
.
Возвратимся к выражению (173) и рассмотрим возможное перемещение по координате k при неизменности остальных механических координат, т.е.
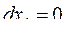 при
при 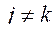 ;
; 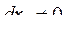
Если в качестве независимых координат приняты переменные 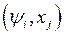 , то выражение полного дифференциала,
, то выражение полного дифференциала,
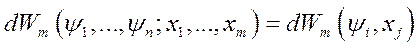 ,
,
при оговоренных условиях, принимает вид
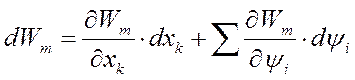
Подставим это значение 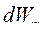 в уравнение закона сохранения энергии (169)
в уравнение закона сохранения энергии (169)
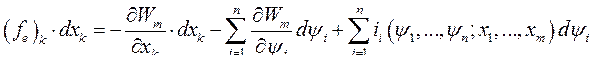 (174)
(174)
В выражение (174) входит сумма частных дифференциалов от энергии магнитного поля по потокосцеплениям контуров электромеханической системы. Эту сумму мы можем рассматривать как полный дифференциал от энергии 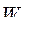 , записанной в форме уравнения (173) в предположении, что все механические координаты имеют свои конечные значения при изменении потокосцеплений от нуля до своих конечных значений. То-есть
, записанной в форме уравнения (173) в предположении, что все механические координаты имеют свои конечные значения при изменении потокосцеплений от нуля до своих конечных значений. То-есть
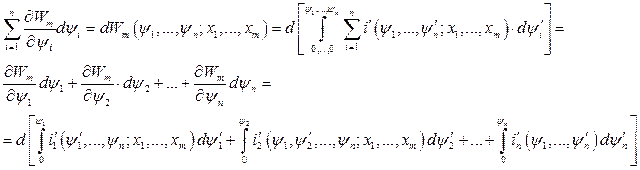
Как известно, дифференциал от интеграла это полный дифференциал, стоящий под знаком интеграла
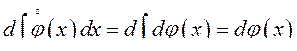
Следовательно,
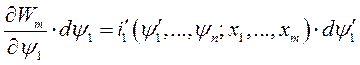 ,
,
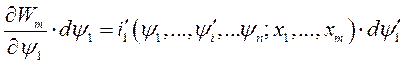 и
и
 (175)
(175)
Подставив выражение (175) в уравнение (173), находим
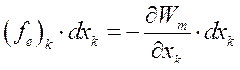 (176)
(176)
А это значит, что обобщенная сила реакции электромеханической системы по обобщенной k – той координате равна взятой со знаком «минус» частной производной от энергии магнитного поля системы по k – той координате
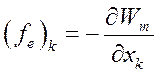 (177)
(177)
При определении обобщенной силы через коэнергию, на основании уравнения (167), имеем:
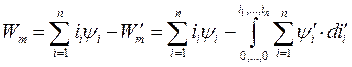 (178)
(178)
Откуда
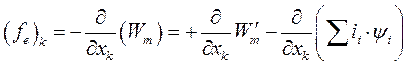 (179)
(179)
Ввиду того, что в сумме 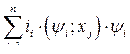 потокосцепления мы рассматриваем как независимые координаты, а функциями
потокосцепления мы рассматриваем как независимые координаты, а функциями 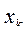 являются токи
являются токи 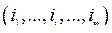 . Следовательно выражение (179) можно переписать в виде
. Следовательно выражение (179) можно переписать в виде
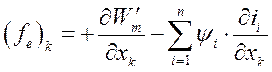 (180)
(180)
Если же в качестве независимых переменных принять токи 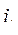 и координаты
и координаты 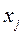 , обобщенную силу мы можем выразить через энергию и коэнергию магнитного поля электромеханической системы, хотя эти выражения будут отличаться от (177) и (180). Вывод этих новых выражений аналогичен проделанному выше и поэтому мы его опускаем, ограничиваясь конечным результатом. Итак, закон сохранения энергии для возможного перемещения
, обобщенную силу мы можем выразить через энергию и коэнергию магнитного поля электромеханической системы, хотя эти выражения будут отличаться от (177) и (180). Вывод этих новых выражений аналогичен проделанному выше и поэтому мы его опускаем, ограничиваясь конечным результатом. Итак, закон сохранения энергии для возможного перемещения 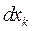 (система консервативна – без потерь)
(система консервативна – без потерь)
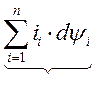
| = | 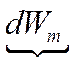
| + | 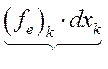
|
| Подведенная электрическая энергия | Запасенная энергия поля | Механическая полезная энергия |
Таблица 1
| Независимые переменные | Сила, выраженная через запасенную энергию | Сила, вычисленная по коэнергии |
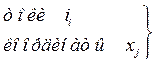
| 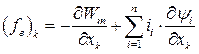
| 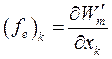
|
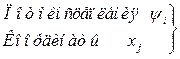
| 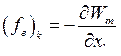
| 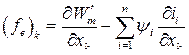
|
Определение электромагнитных моментов
синхронных и асинхронных электрических машин.
Характерной особенностью вращающихся электрических машин является наличие относительно большого (с точки зрения магнитного сопротивления) воздушного зазора в цепях основного магнитного потока. Магнитные потоки рассеяния замыкаются по воздушным путям. А это делает характеристики 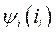 или
или 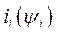 для электромагнитных контуров машин практически линейными. Это в свою очередь означает, что энергия магнитного поля контуров машины равна их коэнергии магнитного поля. Поэтому у вращающихся электрических машин при любом выборе независимых переменных
для электромагнитных контуров машин практически линейными. Это в свою очередь означает, что энергия магнитного поля контуров машины равна их коэнергии магнитного поля. Поэтому у вращающихся электрических машин при любом выборе независимых переменных
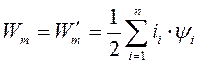 (181)
(181)
Частная производная от энергии магнитного поля по какой-либо механической координате равна эл. магнитной силе, стремящейся изменить эту координату. (Причем под силой подразумевается обобщенная сила, а под координатой – обобщенная координата). Поэтому первая частная производная от  синхронной машины по углу поворота
синхронной машины по углу поворота 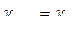 (при постоянстве токов в контурах) равна электромагнитному моменту,
(при постоянстве токов в контурах) равна электромагнитному моменту,
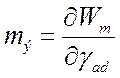 (182)
(182)
Следует иметь в виду, что под 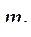 подразумевается тот момент, который производит изменение энергии электромагнитного поля, а не момент, противодействующий этому изменению. Таким образом, этот момент в двигателе, производя вращение ротора в положительном направлении будет положительным, а в генераторе – отрицательным.
подразумевается тот момент, который производит изменение энергии электромагнитного поля, а не момент, противодействующий этому изменению. Таким образом, этот момент в двигателе, производя вращение ротора в положительном направлении будет положительным, а в генераторе – отрицательным.
Асинхронная машина. Рассмотрим 3-х фазную асинхронную машину с фазной обмоткой на роторе. Ниже будет показано, что конструктивные особенности асинхронной машины не влияют на общее выражение её электромагнитного момента. Электромагнитный момент определяем из формулы (182), а энергию магнитного поля находим по выражению (174).
Итак, энергия магнитного поля асинхронной машины
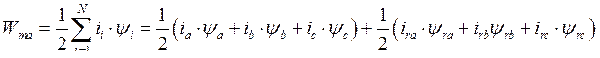
Преобразуем сумму произведений фазных токов на фазные потокосцепления статора и ротора, используя обратное преобразование Парка-Горева, в осях x,y, вращающихся относительно статора с произвольной скоростью,
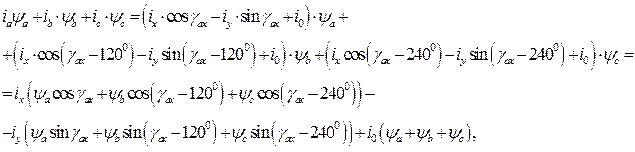
но
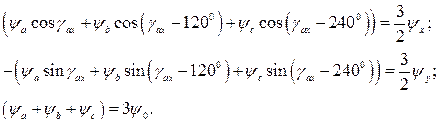
Таким образом,
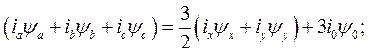 (183)
(183)
по аналогии
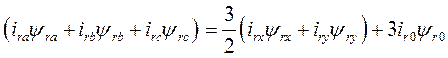 (184)
(184)
Это позволяет выражение (181) переписать в виде
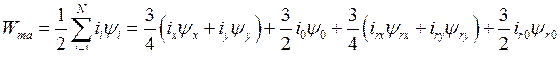 (185)
(185)
Выразим потокосцепления  через токи и реактивности, используя уравнение связи
через токи и реактивности, используя уравнение связи
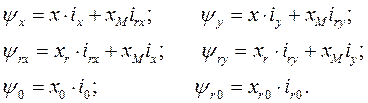
В результате подстановки уравнений связи в (185) выражение энергии магнитного поля электрических контуров асинхронной машины в осях x,y принимает вид
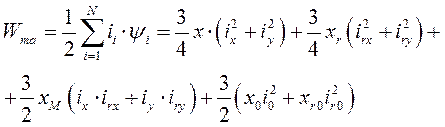 (186)
(186)
Ввиду того, что вывод выражения (186) осуществлялся в ортогональных осях x,y вращающихся с произвольной скоростью, это выражение должно быть справедливым для всех частных случаев, когда скорость вращения ортогональных осей либо заданна, либо фиксирована.
В частности, когда ортогональные оси закреплены роторе машины и вращаются с его скоростью, выражение (185) будет выглядеть как
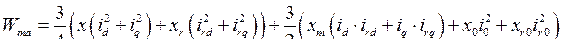 (187)
(187)
Из последнего выражения видно, что энергия магнитного поля асинхронной машины является функцией проекции и.в. токов обмоток статора и ротора, а также токов нулевого чередования фаз.
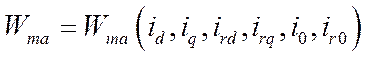
В виду того, что изображающие векторы многофазных величин строятся исключительно в собственных фазных осях, их проекции на произвольные ортогональные оси в общем случае определяются мгновенными значениями фазных величин и углом поворота ортогональных осей относительно соответствующих фазных (прямое преобразование Парка – Горева, (174), (175))
При использовании осей d и q, жестко связанных с ротором.
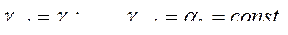
Это значит, что и.в. и их проекции, построенные в фазных осях ротора зависят исключительно от мгновенных значений своих фазных величин, но не зависят от угла поворота ротора, т.к. угол поворота осей, закрепленных на роторе, относительно фазных осей ротора не изменяется. Таким образом, имеем
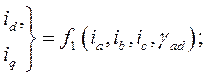
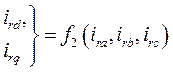 ,
,
но 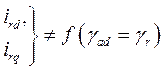
Рассматривая 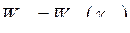 как сложную функцию, отметим, что
как сложную функцию, отметим, что
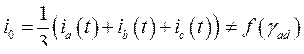 и
и
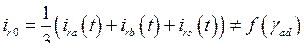 .
.
Отсюда следует:
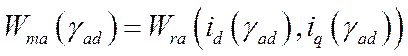 (188)
(188)
Что дает
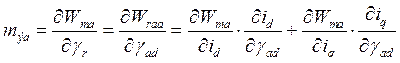 (189)
(189)
Находим частные производные, входящие в (189)
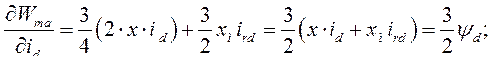
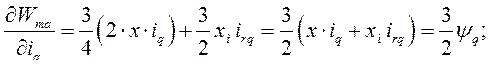
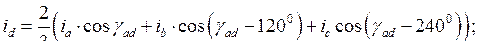
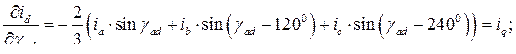
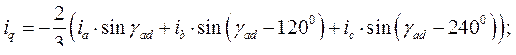
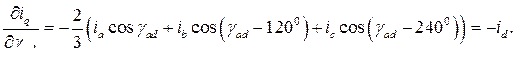
Подставив найденные значения частных производных в выражение (189), получим выражение электромагнитного момента асинхронной машины
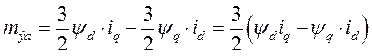 (190)
(190)

Как известно, векторное произведение двух векторов  и
и 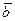 находят по формулам:
находят по формулам:
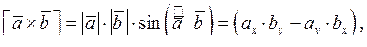 где
где
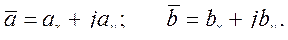
В последних выражениях компоненты векторов по осям берутся со своими знаками.
Следовательно,
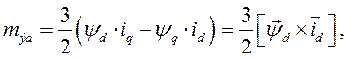 (191)
(191)
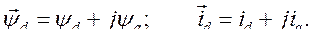
Геометрический смысл векторного произведения
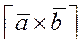
площадь параллелограмма, построенного на векторах  и
и 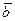 . Векторное произведение положительно, если кратчайший поворот от
. Векторное произведение положительно, если кратчайший поворот от  к
к 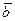 происходит против часовой стрелки, если наоборот – отрицательно.
происходит против часовой стрелки, если наоборот – отрицательно.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|