
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Асинхронная машина. 4 страница
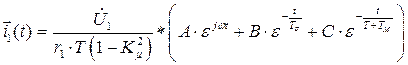 (125)
(125)
где 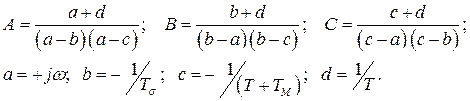
После подстановки в уравнение (125) коэффициентов А,В и С, выраженных через a,b,c,d, и элементарных преобразований получим:
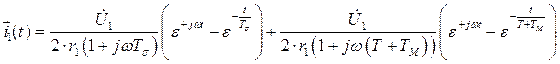 (126)
(126)
Принимая во внимание, что
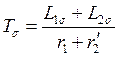 и
и 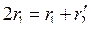 , а также
, а также 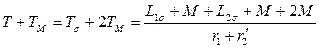 , выражение (126) для и.в. тока
, выражение (126) для и.в. тока 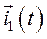 можно привести к виду
можно привести к виду
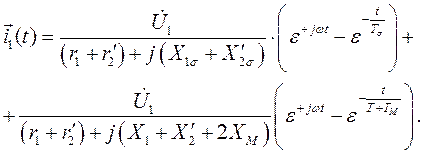 (127)
(127)
В выражении (127)
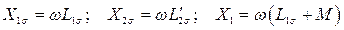 и
и 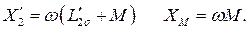
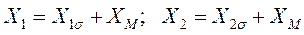
Как известно, сопротивление короткого замыкания асинхронной машины равно
 .
.
Обозначим
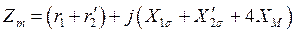 .
.
Это позволяет записать выражение (127) в виде
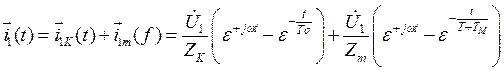 (128)
(128)
где 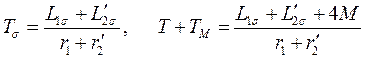
Другими словами, подключение АМ под 3-х фазное синусоидальное напряжение эквивалентно подключению под это напряжение двух независимых 3-х фазных контуров с фазными сопротивлениями ZK и Zm. Схема замещения изображена на рис. 17.
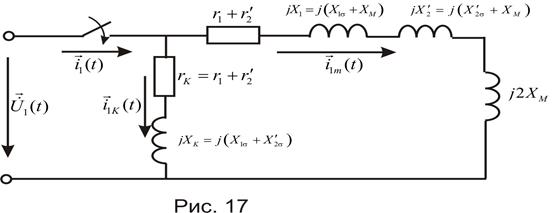
При этом у первого контура достаточно малая индуктивность, определяемая только потоками рассеяния, а у второго индуктивность достаточно велика. Принимая во внимание, что
 , а
, а 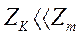
можно утверждать, что нарастание тока в начальный отрезок времени определяется исключительно контуром ZK.
Действительно, параметры асинхронных машин в относительных единицах (о.е.) находится в пределах
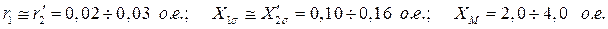
Это значит, что
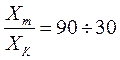 и
и 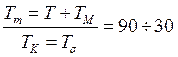
Поэтому во многих случаях при решении задач, связанных с подключением АМ под синусоидальное напряжение, током 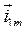 пренебрегают по сравнению с
пренебрегают по сравнению с 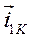 . Из формул (127) и (128), а также из выражений для ZK и Zm следует, что в установившемся режиме
. Из формул (127) и (128), а также из выражений для ZK и Zm следует, что в установившемся режиме
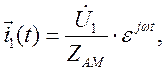 (129)
(129)
где  (130)
(130)
Сопротивление ZAM соответствует известной Т – образной схеме замещения асинхронной машины при неподвижном роторе. Это, собственно говоря, мы и должны были получить, поскольку установившийся режим является частным случаем рассмотренного нами динамического режима.
Найденные закономерности могут быть использованы при решении конкретных технических задач. В частности, покажем это на примере определения максимального провала напряжения при подключении к 3-х фазному синхронному генератору 3-х фазного асинхронного двигателя соизмеримой мощности.
Определение провала напряжения синхронного генератора
при подключении асинхронного двигателя,
мощность которого соизмерима с мощностью генератора
1. Судовые синхронные генераторы являются явнополюсными машинами, на индукторе которых, помимо обмотки возбуждения, размещены успокоительные обмотки (короткозамкнутые контуры) как по продольной, так и по поперечной осям. Поэтому для них в динамических режимах характерен как сверхпереходный, так и переходный процесс. Известно, что наибольший провал напряжения имеет место сразу же после подключения нагрузки, то есть в промежутке времени, пока система АРВ генератора не успеет отреагировать на изменение тока и напряжения. Переходный процесс в якорной обмотке сопровождается изменением тока в обмотке возбуждения и успокоительных контурах и практически вытеснением потока реакции якоря из обмоток индуктора.
Другими словами, данный режим является сверхпереходным, и при этом можно считать, что э.д.с. за сверхпереходной реактивностью 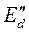 остается постоянной. Это позволяет при анализе режима реальный генератор с изменяющейся э.д.с. Еd и реактивностями Xd и Хq заменить эквивалентными, у которого э.д.с.
остается постоянной. Это позволяет при анализе режима реальный генератор с изменяющейся э.д.с. Еd и реактивностями Xd и Хq заменить эквивалентными, у которого э.д.с. 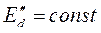 и реактивности Х"d и X"q. В виду того, что сверхпереходные реактивности Х"d и X"q - величины оного порядка, близки друг другу по модулю, вполне допустимо, для данного конкретного случая, генератор рассматривать как неявнополюсный с э.д.с.
и реактивности Х"d и X"q. В виду того, что сверхпереходные реактивности Х"d и X"q - величины оного порядка, близки друг другу по модулю, вполне допустимо, для данного конкретного случая, генератор рассматривать как неявнополюсный с э.д.с.  и реактивностью якорной цепи
и реактивностью якорной цепи
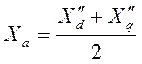
2. Ниже в приложении будет показано, что асинхронный двигатель в режиме подключения (этот режим является режимом внезапного короткого замыкания) замещается активными сопротивлениями и реактивностями рассеяния обмоток статора и ротора.
Поэтому полное сопротивление нагрузки находим как
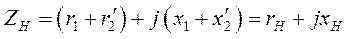
3. Анализ режима производим в ортогональных осях, жестко связанных с ротором генератора. Дифференциальные уравнения записываем в относительных единицах (о.е.). При этом параметры асинхронного двигателя должны быть приведены к базисным величинам генератора.
Тот факт, что мы замещаем реальный явнополюсный генератор эквивалентным неявнополюсным, позволяет записать и решить дифференциальные обобщенные уравнения машин в векторной форме. В качестве основных переменных принимаем изображающие векторы (и.в.) потокосцеплений. В качестве единицы времени принимаем синхронную секунду (с.с.) или радиан (рад.). Тогда
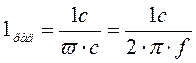
или
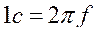 рад;
рад;
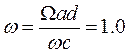 - скорость вращения ротора генератора;
- скорость вращения ротора генератора;
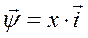 - и.в. потокосцепления, выраженный через и.в. тока;
- и.в. потокосцепления, выраженный через и.в. тока;
здесь х - реактивность (собственная или взаимная) соответствующего контура.
4.Провал напряжения находится в виде и.в. провалов напряжения всех фаз генератора.
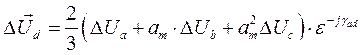
Этот параметр является более информативным по сравнению с провалом напряжения, найденным для какой-либо фазы генератора, поскольку характеризует всю трехфазную систему. Однолинейная расчетная схема представлена на рис. 18.
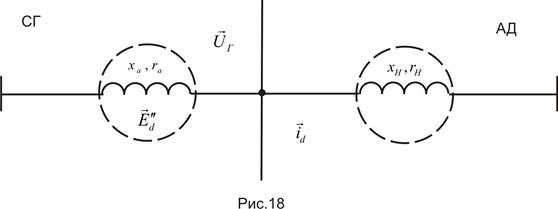
Обобщенные уравнения напряжения в о.е., записанные в осях d, q генератора:
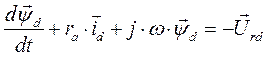 - для генератора;
- для генератора;
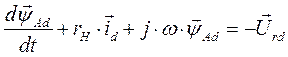 для асинхронного двигателя;
для асинхронного двигателя;
Здесь 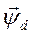 - и.в. потокосцеплений якорной обмотки генератора, записанный в осях d, q;
- и.в. потокосцеплений якорной обмотки генератора, записанный в осях d, q;
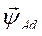 - и.в. потокосцеплений якорной обмотки АД, записанный в осях d, q;
- и.в. потокосцеплений якорной обмотки АД, записанный в осях d, q;
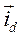 - и.в. токов, протекающих по якорным обмоткам и генератора и асинхронного двигателя, записанный в осях d, q;
- и.в. токов, протекающих по якорным обмоткам и генератора и асинхронного двигателя, записанный в осях d, q;
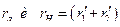 - активные сопротивления соответственно фазы генератора и фазы эквивалентной схемы замещения АД.
- активные сопротивления соответственно фазы генератора и фазы эквивалентной схемы замещения АД.
Результирующее потокосцепление якоря генератора 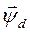 можно рассматривать как геометрическую сумму потокосцеплений от токов индуктора и токов якоря,
можно рассматривать как геометрическую сумму потокосцеплений от токов индуктора и токов якоря,
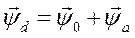 ,
,
где 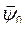 - и.в. потокосцеплений от токов индуктора;
- и.в. потокосцеплений от токов индуктора;
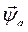 - и.в. потокосцеплений реакций якоря.
- и.в. потокосцеплений реакций якоря.
В относительных единицах 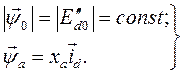 (131)
(131)
Принимая во внимание то, что к АД приложено напряжение генератора 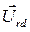 и то, что
и то, что 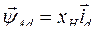 , где xH -реактивность фазы в эквивалентной схеме замещения АД, можно записать уравнение
, где xH -реактивность фазы в эквивалентной схеме замещения АД, можно записать уравнение
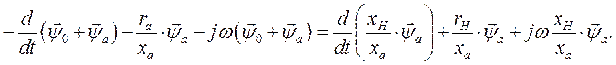
Оно приводится к виду
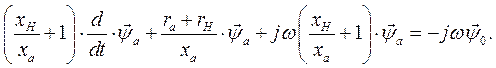 (132)
(132)
В соответствии с первым уравнением системы (131) 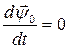 .
.
Обозначим 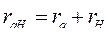
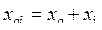 .
.
Умножив все компоненты уравнения (132) на ха, получаем
 (133)
(133)
Запишем дифференциальное уравнение (133) в операторной форме (по Лапласу), принимая во внимание, что  и
и 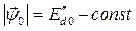 а также
а также 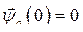 .
.
И обозначив 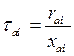 уравнение (133) приводим к виду
уравнение (133) приводим к виду
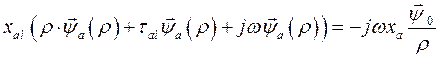
Или
 (134)
(134)
Откуда находим
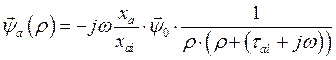 (135)
(135)
Обратное преобразование Лапласа позволяет найти  в виде
в виде
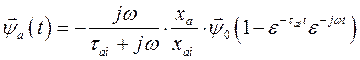 (136)
(136)
Комплексный корень многочлена знаменателя уравнения (135) запишем в показательной форме

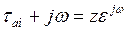 , смотри рис.19
, смотри рис.19
где 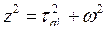 ;
; 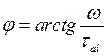 ;
;
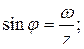
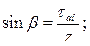
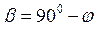
Это позволяет записать уравнение (136) в виде
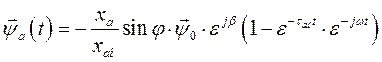 (137)
(137)
Запишем это же выражение для потокосцепления реакции якоря в осях 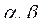 , неподвижных относительно статора генератора
, неподвижных относительно статора генератора
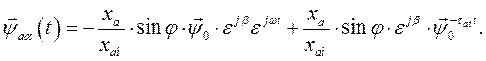 (138)
(138)
Из последнего равенства видно, что потокосцепление реакции якоря содержит две компоненты. Первая из них находится практически в противофазе (угол 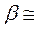 10 град) с потокосцеплением
10 град) с потокосцеплением 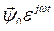 и вращается относительно неподвижных осей с синхронной скоростью.
и вращается относительно неподвижных осей с синхронной скоростью.
Вторая же компонента потокосцепления реакции якоря неподвижна относительно статора и затухает по экспоненциальному закону с постоянной времени
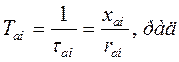 (139)
(139)
Попутно можно отметить, что эта апериодическая составляющая потокосцепления  является причиной появления периодических затухающих токов в обмотках ротора генератора и создает тормозной электромагнитный момент, по своему характеру не отличающийся от электромагнитного момента в режиме динамического торможения асинхронных двигателей. С той лишь разницей, что этот момент достаточно быстро затухает. И.в. падения напряжения достаточно просто найти, не находя потокосцепление реакции якоря, а имея только его изображение
является причиной появления периодических затухающих токов в обмотках ротора генератора и создает тормозной электромагнитный момент, по своему характеру не отличающийся от электромагнитного момента в режиме динамического торможения асинхронных двигателей. С той лишь разницей, что этот момент достаточно быстро затухает. И.в. падения напряжения достаточно просто найти, не находя потокосцепление реакции якоря, а имея только его изображение 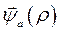 . Действительно,
. Действительно, 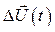 является результатом изменения потокосцепления
является результатом изменения потокосцепления 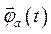 и падения напряжения на активном сопротивлении обмотки статора
и падения напряжения на активном сопротивлении обмотки статора
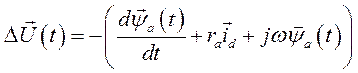 (140)
(140)
Поэтому в операторной форме и в осях d, q можно записать
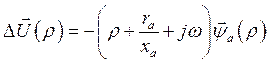 ,
,
Или обозначив 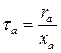 и используя уравнение (135), имеем:
и используя уравнение (135), имеем:
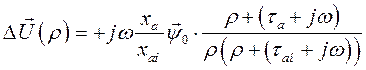 (141)
(141)
Обозначим 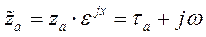
и применив к выражению (141) обратное преобразование Лапласа, находим и.в. падения напряжения как функцию времени в виде
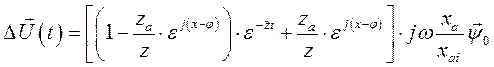 (142)
(142)
или
 (143)
(143)
Принимая во внимание, что 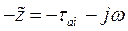 , из выражения (142) следует, что
, из выражения (142) следует, что 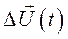 имеет две составляющие. Одна из них
имеет две составляющие. Одна из них
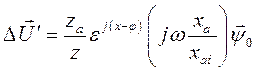 (144)
(144)
оставаясь неизменной, вращается вместе с осями d, q, а вторая
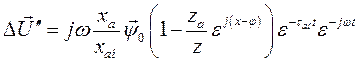 , (145)
, (145)
затухая по экспоненциальному закону с постоянной времени  , остается неподвижной относительно осей статора.
, остается неподвижной относительно осей статора.
Из выражения (143) видно, что первоначальный провал напряжения равен
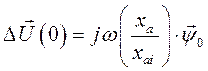 (146)
(146)
Взаимное расположение векторов 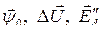 и
и 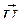 при
при 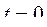 представлено на рис.3.
представлено на рис.3.
Значительно проще находится и.в. падения напряжения 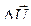 , если не учитывать влияние активного сопротивления обмотки статора на его величину. Это допущение можно считать вполне обоснованным, поскольку активное сопротивление
, если не учитывать влияние активного сопротивления обмотки статора на его величину. Это допущение можно считать вполне обоснованным, поскольку активное сопротивление 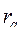 на порядок меньше расчетного сопротивления
на порядок меньше расчетного сопротивления 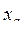 и на величину модуля полного сопротивления практически не влияет.
и на величину модуля полного сопротивления практически не влияет.
Действительно
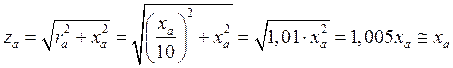
В этом случае и.в. падения напряжения находится как производная от и.в. потокосцепления реакции якоря, взятая с обратным знаком.
Во вращающихся осях это будет иметь вид
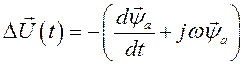 (147)
(147)
А в осях, неподвижных относительно статора -
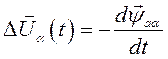 (148)
(148)
Подставив в уравнение (148) 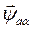 из выражения (138), имеем
из выражения (138), имеем
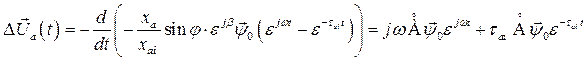 (149)
(149)
Здесь 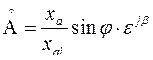
Для того, чтобы получить вектор падения напряжения в осях d, q, жестко связанных с ротором, можно воспользоваться либо выражением (147), либо достаточно выражением (148) умножить на 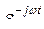
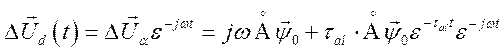 (150)
(150)
Легко убедиться, что мы придем к тому же результату, подставив в (146) 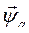 из формулы (137).
из формулы (137).
Принимая во внимание, что
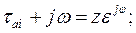
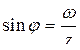 и
и 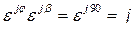 находим
находим
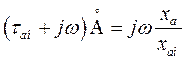
А это значит, что из выражений (149) и (150) первоначальный провал напряжения находим как
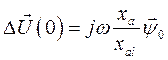 (151)
(151)
То есть, первоначальный провал напряжения, найденный при не учете активного сопротивления якорной обмотки генератора, имеет ту же величину, что и в случае учета данного сопротивления, формула (146). С позиции физики явления такой результат является закономерным. Действительно, при t = 0 токи в якорных обмотках машин, а также потокосцепления, связанные с ними, равны нулю. В то же время производные от токов и потокосцеплений не равны нулю. Следовательно, при t = 0 э.д.с. генератора уравновешивается падением напряжения на реактивностях расчетной цепи.
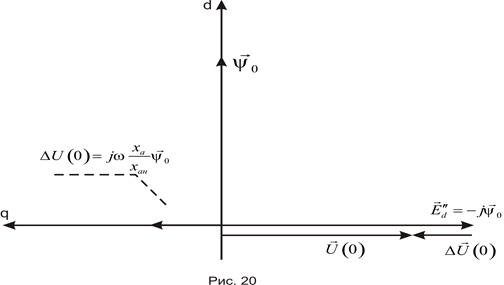
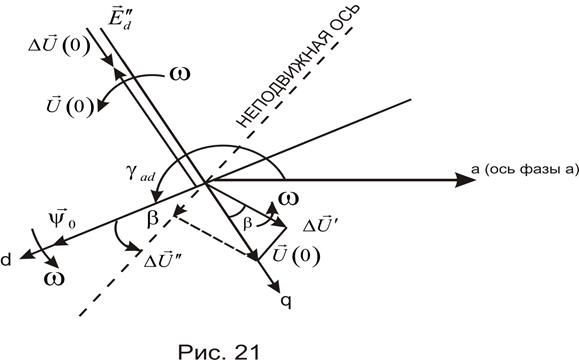
Рассмотрим и.в. падения напряжения 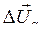 , записанный в неподвижных осях, выражение (149), рис.21.
, записанный в неподвижных осях, выражение (149), рис.21.
Из выражения (149) следует, что и.в. 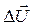 равен геометрической сумме двух векторов
равен геометрической сумме двух векторов 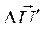 и
и 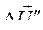
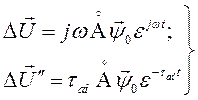 (152)
(152)
Первый из них 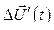 вращается вместе с ротором, оставаясь неизменным по модулю, а второй,
вращается вместе с ротором, оставаясь неизменным по модулю, а второй, 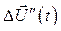 , оставаясь неподвижным относительно статора, затухает по экспоненциальному закону. Как видно на рис.21, их начальное положение относительно статора определяется положением ротора в момент подключения нагрузки. При
, оставаясь неподвижным относительно статора, затухает по экспоненциальному закону. Как видно на рис.21, их начальное положение относительно статора определяется положением ротора в момент подключения нагрузки. При 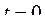 ,
, 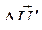 и
и 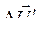 находятся в квадратуре и по мере поворота ротора угол между ними увеличивается. Через четверть периода
находятся в квадратуре и по мере поворота ротора угол между ними увеличивается. Через четверть периода
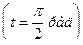 эти векторы будут в противофазе, а еще через пол периода
эти векторы будут в противофазе, а еще через пол периода 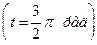 совпадут по фазе. Именно в этот момент (или близкий к нему) следует ожидать наибольшего провала напряжения. Хотя при большой скорости затухания вектора
совпадут по фазе. Именно в этот момент (или близкий к нему) следует ожидать наибольшего провала напряжения. Хотя при большой скорости затухания вектора 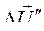 может казаться, что провал напряжения, при
может казаться, что провал напряжения, при 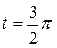 меньше
меньше 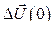 .
.
Рассмотрим в качестве примера подключение с режима холостого хода к синхронному генератору асинхронного двигателя, мощность которого в 4 раза меньше мощности генератора. Параметры генератора в о.е.:
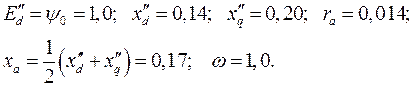
Параметры АД, приведенные к генератору, в о.е.
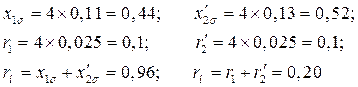
Расчетные параметры в о. е.:
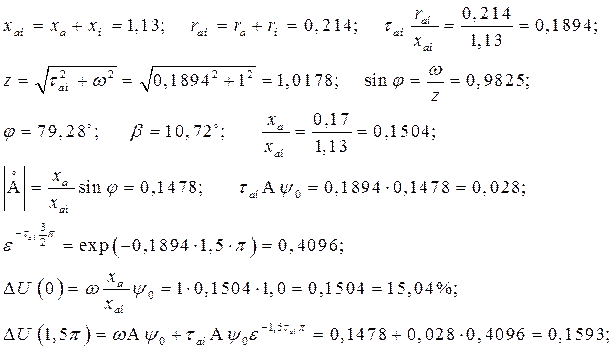
Таким образом , 
И.в. 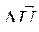 при учете падения напряжения на активном сопротивлении якорной обмотки генератора может быть найден либо из формулы (143) либо из выражения
при учете падения напряжения на активном сопротивлении якорной обмотки генератора может быть найден либо из формулы (143) либо из выражения
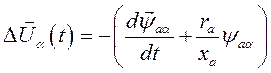 (153)
(153)
Используя выражение (138) и обозначив 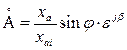 , имеем
, имеем
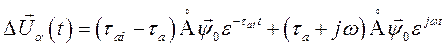 (154)
(154)
где 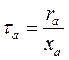
Подставим в уравнение (154) параметры из предыдущего примера для 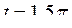 и получим
и получим
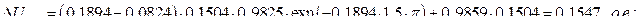
таким образом, 
Парадокс в том, что максимальный провал напряжения, найденный при учете падения напряжения на активном сопротивлении цепи якоря генератора, оказывается меньше, чем та же величина, найденная при не учете этого напряжения.
Хотя на самом деле результат закономерен и связан с появлением в машинах неподвижных относительно якорных обмоток затухающих магнитных потоков, а следовательно, затухающих постоянных токов. И.в. потокосцепления реакции якоря  и связанный с ним и.в. токов якоря
и связанный с ним и.в. токов якоря 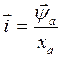 имеют периодические и апериодические составляющие, каждая из которых создает свое падение напряжения. При этом падения напряжения на активном сопротивлении и реактивности от апериодических составляющих вычитаются, а от периодических составляющих складываются геометрически (сравним выражения (149) и (154)). И в результате оказывается, что уменьшение одной составляющей больше увеличения второй.
имеют периодические и апериодические составляющие, каждая из которых создает свое падение напряжения. При этом падения напряжения на активном сопротивлении и реактивности от апериодических составляющих вычитаются, а от периодических составляющих складываются геометрически (сравним выражения (149) и (154)). И в результате оказывается, что уменьшение одной составляющей больше увеличения второй.
Уравнение токов АМ и её схема замещения при подключении
под 3-х фазное напряжение.
Подключение асинхронной машины к источнику 3-хфазного синусоидального напряжения в виду того, что магнитные проводимости асинхронной машины одинаковы по всем осям, обобщенные уравнения напряжений статорной и роторной обмоток асинхронной машины могут быть записаны в любых ортогональных осях, в том числе и осях, неподвижных относительно статора. Для машины, у которой параметры обмотки ротора приведены к параметрам обмотки статора, уравнения, записанные в осях, закрепленных на статоре, имеют вид:
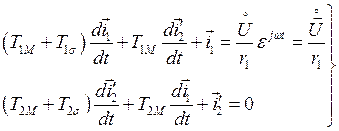 (155)
(155)
Здесь 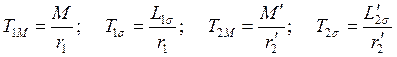
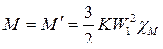 - коэффициент взаимоиндукции приведенной асинхронной машины (АМ)
- коэффициент взаимоиндукции приведенной асинхронной машины (АМ)
В виду того, что у правильно спроектированной АМ 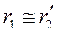 и
и 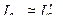 , принимаем
, принимаем
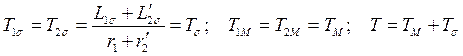 или
или 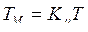
Запишем уравнения (155) в операторной форме, имея в виду, что 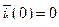 и
и 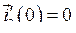 .
.
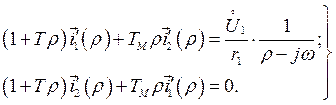 (156)
(156)
Решая уравнения (156) относительно 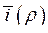 , находим
, находим
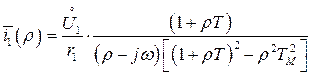 (157)
(157)
Найдем корни уравнения
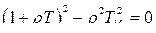
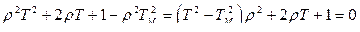
Учитывая, что 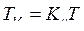 , запишем
, запишем
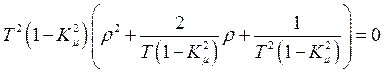 (158)
(158)
Корнями выражения в скобках уравнения (158) будут
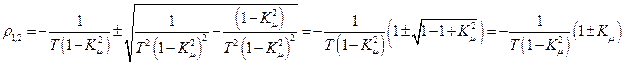
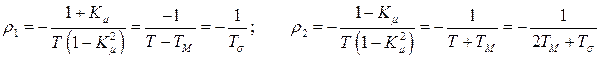
Найденные корни уравнения (158) позволяют записать уравнение (157) в виде
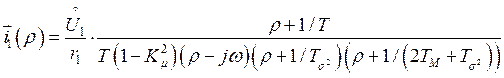 (159)
(159)
Откуда, пользуясь обратным преобразованием Лапласа, находим в виде
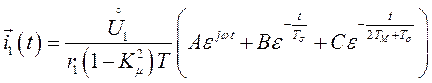 (160)
(160)
Где
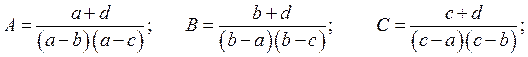
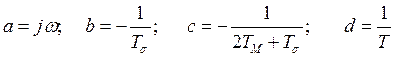
После подстановки и элементарных преобразований имеем
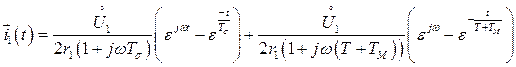 (160а)
(160а)
Или, выражая постоянные времени через соответствующие индуктивности и активные сопротивления, выражение (160) можно записать в виде
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|