Асинхронная машина. 1 страница

Понятие о изображающем векторе

многофазных величин

Необходимость введения понятия «изображающий вектор» возникла при анализе работы электрических машин в различных электрических и электромеханических системах. Замечательной особенностью изображающего вектора (и. в.) является то, что он может служить для характеристики величин, имеющих как полевой характер, так и для величин, представленных в виде ограниченного множества дискретно распределенного в пространстве.

Физической предпосылкой к введению понятия «изображающий вектор» служит общеизвестный факт, что в электрической машине существует единое магнитное поле, являющееся результатом совокупного действия токов, протекающих по всем её обмоткам.

Пренебрегая краевыми эффектами на торцах магнитного ядра машины, единое электромагнитное поле в зазоре электрической машины можно считать плоско – параллельным. Следовательно, его можно изобразить в виде некоторого пространственного вектора в осях машины. С другой стороны, поскольку электромагнитное поле проявляется во всем рассматриваемом объеме электрической машины, изобразить его в виде единственной векторной величины можно чисто условно, отразив всего два его наиболее характерных признака (параметра) (в частности для магнитного поля это могут быть величина магнитного потока и направление вектора максимальной магнитной индукции относительно осей машины, либо два любых других параметра). Поэтому вектор (о котором речь) получил название «изображающий вектор».

Наиболее просто понятие о и.в. получить, рассматривая трехфазную систему переменных величин, например токов.

Пусть по фазным обмоткам a, b, c электрической машины протекают токи ia(f), ib(f), ic(f), являющиеся функциями времени.

На рис. 1 в плоскости поперечного сечения машины представлены пространственные оси фазных обмоток рассматриваемой машины.

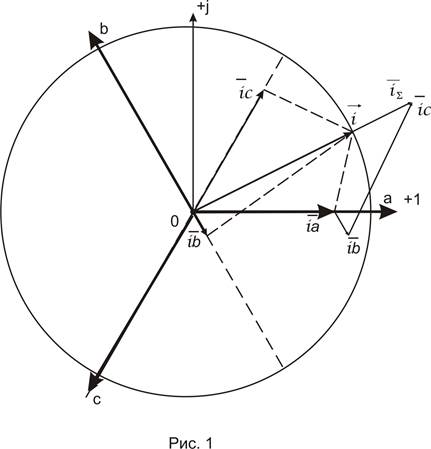
Следует сразу же оговориться, что в качестве положительного направления вращения принято направление против часовой стрелки. Поле в зазоре машины, вращаясь в положительном направлении, достигает максимума своей интенсивности последовательно в фазах a, b, и c. Поэтому при положительном обходе зазора машины за осью фазы a должна следовать ось фазы b и т.д.

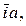
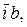
Обозначим 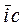- пространственные векторы, модули которых в принятом масштабе равны мгновенным значениям соответствующих фазных токов, а направления совпадают с направлениями осей соответствующих фазных обмоток, если токи положительны и меняют направления на противоположные когда токи отрицательны.

По определению и.в. тока (точнее и.в. трехфазной системы токов), построенный и записанный в координатной системе фазных осей машины, равен 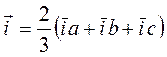или (1)

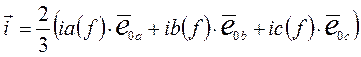, (2) где 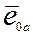, , 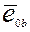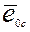- орты соответствующих фазных осей.

Примечание. В m – фазной системе соответствующий и.в. по определению равен

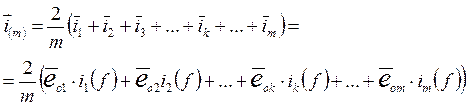(3)

Здесь 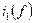, , 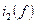… 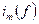- мгновенные значения токов в соответствующих фазах

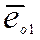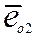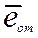, , … , - орты соответствующих фазных осей.

Возвращаемся к 3-х фазной системе. Если рассматривать плоскость фазных осей как комплексную, совместив в частном случае ось действительных величин с осью фазы a , орты фазных осей симметричной трехфазной машины могут быть представлены выражениями:

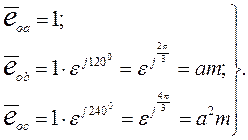(4)

В выражениях (4) 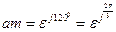- оператор поворота на треть окружности или 120⁰. При этом

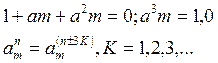
Таким образом, и.в. тока, построенный в фазных осях машины, в принятой комплексной плоскости можно выразить уравнением

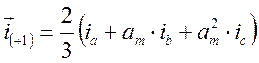(5)

Прямое и обратное преобразование

Парка – Горева.

Смысл преобразования Парка – Горева заключается в нахождении формул, позволяющих и.в., построенных в фазных осях машины, записать в ортогональных осях , вращающихся с произвольной скоростью относительно фазных осей. Рассмотрим две координатные системы с общим началом:

a, b, c – система неподвижных фазных осей машины и x, y – система ортогональных осей, вращающихся относительно первой с некоторой произвольной скоростью Ωax (рис. 2). Здесь 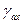- угол между осью фазы a и

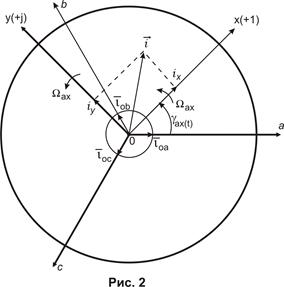осью x. В общем случае

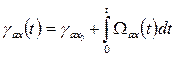(6)

В уравнении (6) сделан прозрачный намек на то обстоятельство, что скорость вращения осей x, y относительно фазных осей машины вовсе не обязана быть постоянной.

Запишем и.в. тока 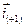, формула (5), построенный в фазных осях машины, во вращающихся ортогональных осях x, y. Это означает, что в осях x и y необходимо записать компоненты и.в. (5)

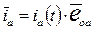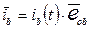, и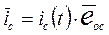

Каждый из пространственных векторов 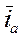, 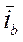и 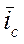равен произведению своего модуля на орт, определяющий направление. Поскольку модуль вектора не меняется при переходе от одних осей к другим, а меняться может только ориентация вектора по отношению к новой координатной системе, следовательно, для записи вектора в осях x, y достаточно записать в этих осях его орт. Обозначим 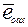, , 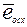- орты осей a, b, c машины, записанные в осях x, y.

Если рассматривать плоскость осей x, y в качестве комплексной, приняв в качестве действительной ось x, а мнимой – y, можно записать:

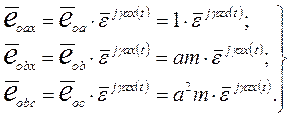(7)

Таким образом, пространственные векторы фазных токов машины, построенные в собственных фазных осях, но записанные во вращающихся осях x и y имеют вид:

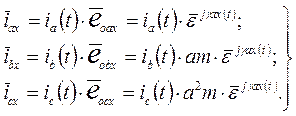(8)

Сам изображающий вектор тока, записанный в осях x, y, принимает вид

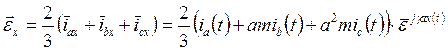(9)

Из формулы (9) следует: для записи и.в., построенного и записанного в собственных фазных осях, в новых, вращающихся с произвольной скоростью, достаточно исходный и.в. умножить на оператор поворота, exp[-jγax(t)], исходной системы осей относительно новых, x, y. В осях x, y и.в. имеет компоненты по осям: i_x и i_y.

В комплексной форме можно записать

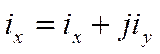. (10)

Перепишем выражения (8), используя формулу Эйлера:

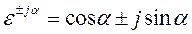а именно:

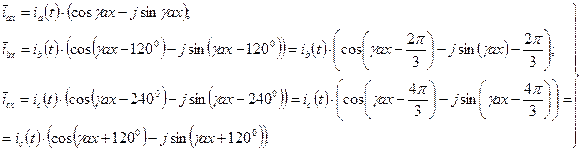(11)

Как известно, два комплексных числа равны тогда и только тогда, когда равны между собой их действительные и мнимые части. Аналогично для векторов можно утверждать: два вектора равны друг другу, когда равны между собой их проекции на выбранные координатные оси. На основании этих правил, используя выражения (9), (10) и (11), для действительной и мнимой части комплекса 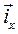можем записать:

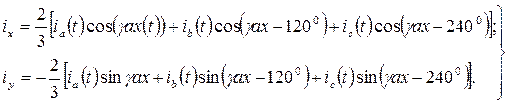(12)

По существу, система (12) является прямым преобразованием Парка – Горева и связывает проекции и.в. на ортогональные оси, вращающиеся с произвольной скоростью Ωax(t), с мгновенными значениями переменных фазных величин. Следует помнить, что γax(t), входящая в эти выражения, является в общем случае функцией времени (6). Формулу преобразования Парка – Горева часто записывают в матричной форме:

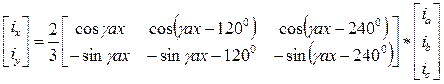(13)

Для нахождения мгновенных значений фазных величин используют обратное преобразование Парка – Горева, которое можно получить, дополнив уравнение (13) выражением для тока нулевого чередования фаз 3 – х фазной системы

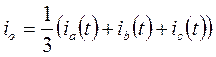(14)

и разрешив полученные уравнения относительно фазных токов. В результате получаем обратное преобразование Парка – Горева

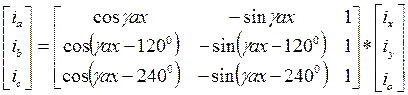(15)

Здесь уместно сделать ряд замечаний:

1) введение уравнения (14) имеет, в известной степени, формальный характер и служит исключительно для придания определенности обратному преобразованию Парка – Горева; величины нулевого чередования фаз изображающих векторов не имеют, т.к. геометрическая сумма их пространственных векторов равна нулю;

2) в случае несимметричной многофазной системы последняя может быть разложена на симметричные и для систем прямого и обратного чередования фаз можно построить свои изображающие векторы.

Изображающий вектор симметричной 3 – х фазной системы токов.

Плоскость фазных осей машины будем рассматривать как комплексную, совместив ось действительных (+1) с осью фазы a. Пусть токи в фазных обмотках изменяются по синусоидальному закону и ток фазы a при t=0 равен амплитудному значению. При этом условии законы изменения токов в фазах запишутся в виде:

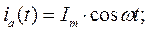
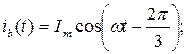
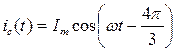Запишем cosαв виде 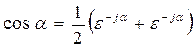, тогда

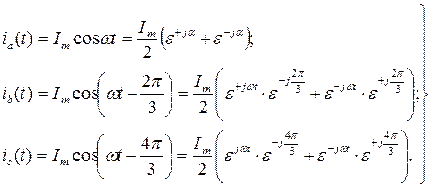(16)

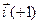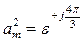
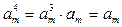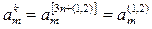Подставим найденные выражения фазных токов (16) в уравнение (5) для помня при этом, что , и и .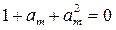

Таким образом, имеем:

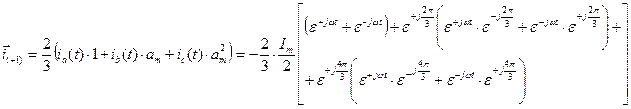Разделим в последнем выражении слагаемые содержащие , а также произведем элементарные упрощения

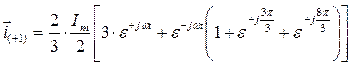, но

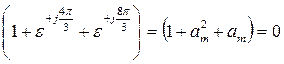, следовательно

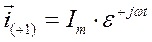(17)

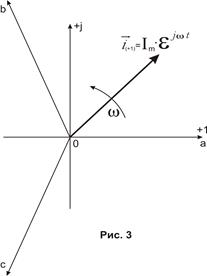
Таким образом, можно сделать вывод, что и.в. симметричной 3 – х фазной системы переменных величин – это вращающийся вектор, модуль которого остается постоянным и равным амплитуде фазной величины, а скорость вращения относительно фазных осей равна угловой частот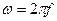е, , где 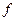- частота изменения фазных величин. Легко доказать, что это же распространяется и на изображающие векторы m – фазных систем.

Опять же на примере и.в. 3 – х фазной системы токов покажем, что проекция и.в. на фазную ось дает (равна) мгновенному значению переменной данной фазы. Действительно, по определению скалярного произведения двух векторов

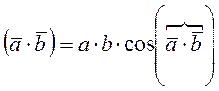Поэтому проекцию и.в. на какую-либо ось находим как скалярное произведение соответствующего и.в. на единичный орт оси.

Если векторы на плоскости заданы своими координатами: 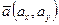и , то (18)

Проекции 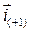на ось фазы a равна

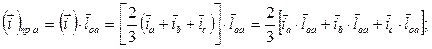
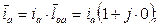
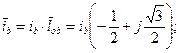
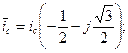
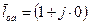
Считая ось действительных осью x, а мнимых – y, находим:

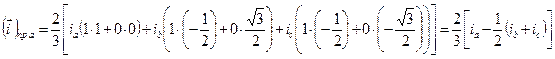(19) но при отсутствии токов нулевого чередования фаз, которые изображающего вектора не имеют,

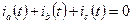или

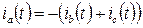(20)

Подставив (20) в (19), имеем

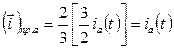(21)

Аналогично можно доказать, что

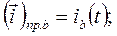
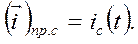(22)

Обобщенные уравнения для напряжений многофазных обмоток машин переменного тока.

Рассмотрим 3-х фазную якорную обмотку синхронной или асинхронной машины. Уравнения напряжений, приложенных к фазным обмоткам имеют вид:

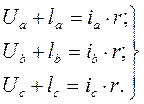
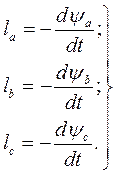
Следовательно,

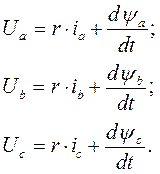(23)

Здесь U_a, U_b, U_c – напряжения (мгновенные значения), приложенные к фазным обмоткам из внешней цепи; i_a, i_b, i_c – токи в фазных обмотках;

ψ_a, ψ_b, ψ_c – потокосцепления соответствующих фазных обмоток.

r – активное сопротивление каждой из фазных обмоток (считаем их симметричными).

По определению и.в. напряжений, потокосцеплений и токов, построенные в фазных осях машины и записанные в произвольной ортогональной координатной системе x, y, равны:

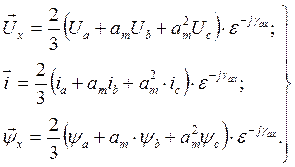(24)

Найдем производную по времени от и.в. 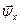, помня, что функциями времени являются как потокосцепления фазных обмоток, ψ_a, ψ_b, ψ_c, так и угол γ_ax(t).

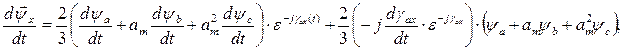
откуда

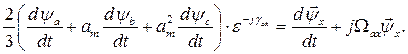(25)

Здесь 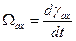- мгновенное значение угловой скорости координатных осей x, y относительно осей a, b, c, в которых построены изображающие векторы.

Подставим выражения (23) в уравнение для 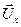из (24)

Используя выражения (24) и (25), получаем

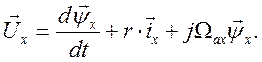(26)

Выражение (26) является обобщенным уравнением для напряжений обмоток машины переменного и постоянного тока, записанное в векторной форме. При использовании этого уравнения необходимо помнить, что 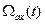- мгновенное значение угловой скорости координатных осей x, y , в которых записаны изображающие векторы, относительно фазных осей, в которых эти векторы построены.

Рассматривая плоскость осей x, y как комплексную, где x – ось действительных, а ось y – мнимых, каждый из и.в. 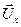, 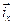и 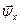можем записать в виде, рис.2

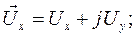
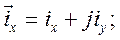
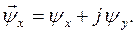(27)

Подставим выражения (27) в уравнение (26) и выделим действительные и мнимые величины. Известно, что два комплекса равны тогда и только тогда, когда равны между собой их действительные и мнимые части. После элементарных преобразований имеем:

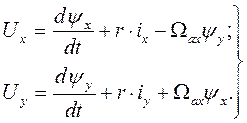(28)

Таким образом, вместо одного векторного уравнения (26) получили два скалярных уравнения (28).

Все разнообразие частных случаев записи обобщенного уравнения определяется выбором осей, в которых записываются изображающие векторы и осей, в которых эти векторы строятся.

Если исследуются электродинамические процессы, и.в. всегда должны строиться в фазных осях того элемента эл. Машины (статор, ротор), которому принадлежат соответствующие фазные величины. Записывать же изображающие векторы можно в любых осях из условия наиболее простого решения конкретной задачи.

Существуют общепринятое обозначение ортогональных осей, а именно:

α, β – оси, неподвижные относительно фазных осей;

d, q – оси, жестко закрепленные на роторе;

U, V – оси, вращающиеся с синхронной скоростью относительно фазных осей;

x, y – оси, вращающиеся с произвольной скоростью относительно фазных.

Физический смысл элементов обобщенного уравнения.

По определению 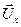является и.в. многофазной системы напряжений внешних по отношению к многофазной обмотке.

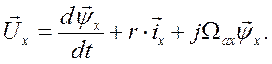
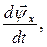
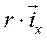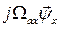Отсюда вытекает, что и являются компонентами 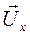, уравновешивающие соответствующие падения напряжения и Э.Д.С. Говорить об их физическом смысле весьма затруднительно, поскольку сами по себе изображающие векторы являются математическими образами, математическими моделями реальных физических величин. Поэтому приходится прибегать к аналогиям. Обратимся к одному из уравнений (23)

Здесь U_a – внешнее напряжение, приложенное к фазе a;

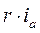- его составляющая, уравновешивающая падение напряжения на активном сопротивлении фазной обмотки;

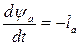- составляющая напряжения, уравновешивающая Э.Д.С., которая индуктируется в фазе a изменяющимся по оси фазы потокосцеплением.

Исходя из этих соображений, будем называть 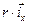падением напряжения на активном сопротивлении фазы при протекании по ней тока .

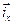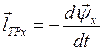- Э.Д.С. от изменяющегося и.в. потокосцеплений 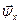трансформаторного характера,

а 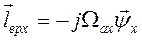- Э.Д.С. вращения и.в. вместе с осями x, y.

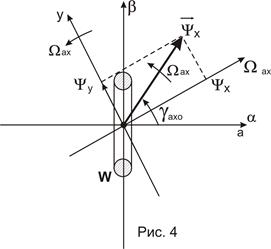Рассмотрим пример. Пусть и.в. потокосцеплений неподвижной обмотки W построен во вращающихся осях x и y и в этих осях неизменен по величине и положению, рис. 4. относительно оси обмотки его можно записать в виде

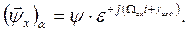              (29)

В обмотке W это потокосцепление будет индуктировать Э.Д.С.

                   (30)

Сравнивая выражение (30) с , приходим к выводу о их полной аналогии. Однако имеется и существенная разница. Говоря о 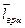, мы эту Э.Д.С. связываем с вращающимся относительно неподвижной обмотки потокосцеплением , а говоря о Э.Д.С. вращения 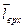, последняя связывается со скоростью вращения осей x и y относительно неподвижных осей многофазной обмотки. То-есть, выбрав оси, для которых 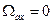, избавляемся от Э.Д.С. вращения в обобщенном уравнении. Тем не менее, это противоречие кажущееся, поскольку, не зависимо от того, в каких осях записано обобщенное уравнение напряжений, обобщенная Э.Д.С. в общем случае равна

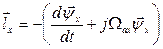                                                                                    (31)

Выбирая те или иные ортогональные оси, мы можем избавиться либо от первого, либо от второго слагаемого в выражении (31), но чаще всего в обобщенном уравнении напряжений присутствуют обе составляющие Э.Д.С.

Рабочая система единиц.

При выполнении расчетов электроэнергетических систем привычными для нас являются Вольты, Амперы, Омы или относительные единицы (о.е.). В обобщенные уравнения напряжений входят потокосцепления, измеряемые в Веберах = .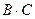

Для удобства, с целью упрощения расчетов, обобщенные уравнения преобразуют таким образом, что потокосцепления приобретают размерность – Вольты, а время становиться безразмерным с размерностью о.е. или радиан. Это достигается достаточно просто: элементы в правой части уравнения (31) умножаются и делятся на базисную или синхронную частоту

.

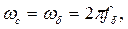
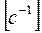В результате получаем

Переходя к размерностям, имеем:

или

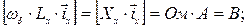
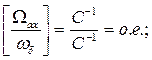
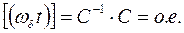
Таким образом, в дальнейшем, используя уравнения напряжений, если не будет специально оговорено, принимаем, что

, Вольт, 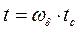, радиан = о.е., 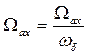, о.е.

Уравнения электрического и механического

состояния синхронной и асинхронной машины

в ортогональных осях.

Обобщенное уравнение напряжений многофазных обмоток позволяет записать уравнения электрического равновесия в ортогональной системе осей, вращающихся с произвольной скоростью, для любой электрической машины. Однако при записи уравнений необходимо учитывать конструктивные особенности машины и выбирать оси, в которых магнитные проводимости машины остаются неизменными независимо от положения ротора. Это есть условием получения полной системы дифференциальных уравнений с постоянными коэффициентами при переменных функциях.

12 3 4 5 6 7 8 9 10 Следующая ⇒