Хелпикс

Главная

Контакты

Случайная статья



Обыкновенные дифференциальные уравнения.

⇐ ПредыдущаяСтр 14 из 28Следующая ⇒


2. Обыкновенные дифференциальные уравнения.

2.1. Задачи, приводящие к дифференциальным уравнениям (ДУ). ДУ 1-го порядка. Частные и общее решения ДУ, интегральные кривые. Задача Коши и теорема существования и единственности ее решения. Особые точки и особые решения ДУ.

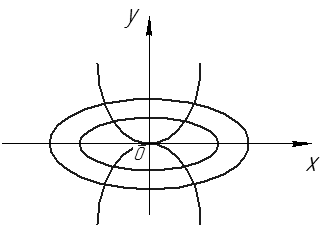
Рис. 30

Рассмотрим на плоскости семейство эллипсов

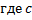 – произвольная положительная постоянная (см. рис. 30).

Найдем семейство кривых, ортогональных семейству эллипсов.

1. Составим дифференциальное уравнение (ДУ) семейства эллипсов.

Продифференцируем уравнение (2.1.1), считая :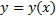

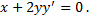
Отсюда 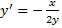 - ДУ семейства эллипсов.  Тогда =

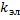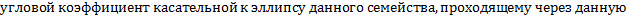
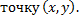
2. Составим ДУ ортогонального семейства. В т. 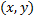 угловой коэффициент касательной должен быть равен 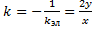, т.е. ДУ ортогонального семейства:

.

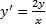3. Найдем уравнение ортогонального семейства:

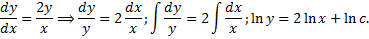
Получаем 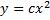 – семейство парабол.

Обыкновенное ДУ 1-го порядка  -

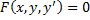, где 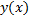 – неизвестная функция;  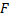– функция 3-х переменных.

ДУ 1-го порядка, разрешенные относительно производной:

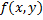 – определена в области .

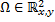Опр. Частным решением ДУ (2.1.2) называется функция 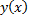, определенная на 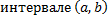, при подстановке которой в ДУ (2.1.2) оно обращается в тождество на 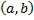, т.е. .

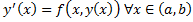Пример.

.

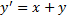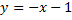 – частное решение, т.к.  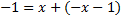– тождество;

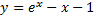 – также частное решение, т.к.  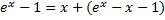– тождество.

Опр. График частного решения 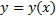 ДУ 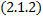называется интегральной кривой ДУ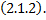

Опр. Равенство 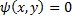, неявно задающее решение ДУ  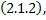называется частным интегралом ДУ .

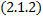Задача Коши для ДУ 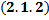: найти частные решения ДУ 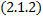, удовлетворяющие начальному условию 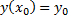, где  ,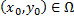

т.е. задача Коши может быть записана следующими образом:

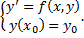
Геометрический смысл: найти интегральную кривую ДУ 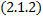, проходящую через т. .


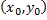⇐ Предыдущая9101112131415161718Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.