Контакты

Случайная статья

Вычисление длин дуг кривых и площадей поверхностей вращения

⇐ ПредыдущаяСтр 13 из 28Следующая ⇒

1.10. Вычисление длин дуг кривых и площадей поверхностей вращения

Длина дуги кривой.

Пусть дуга задана параметрическими уравнениями:

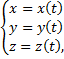
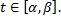
Функции 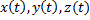имеют на 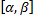непрерывные производные.

,

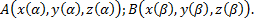
Рассмотрим переменную точку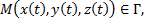

– переменная дуга длиной .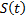

Дифференциал дуги

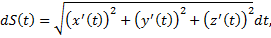
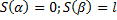– длина всей дуги.

Случай плоской кривой:

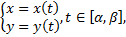
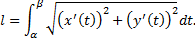
Случай графика функции :

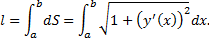
Случай кривой, заданной в полярных координатах:

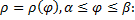
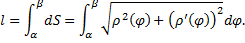
Площадь поверхности вращения.

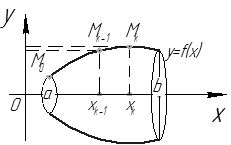
Рис. 29

Рассмотрим функцию 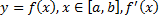– непрерывна на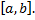

Пусть – дуга графика 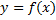– вращается вокруг оси 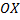. Рассмотрим ломаную 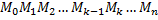, вписанную в дугу , где 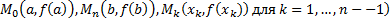(см. рис. 29).

При вращении вокруг 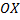звена ломаной 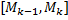получим боковую поверхность усеченного конуса.

Опр. Площадью поверхности вращения называется предел сумм площадей боковых поверхностей усеченных конусов, полученных при вращении вписанной ломаной, при стремлении к 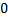максимальной длины звена ломаной.

Площадь боковой поверхности усеченного конуса с радиусами основани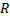й и 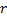и образующей 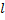равна

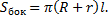
В данном случае

,

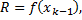
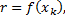
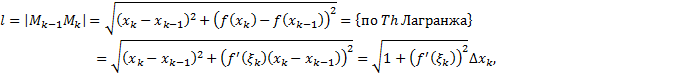
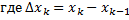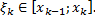
Тогда площадь боковой поверхности усеченного конуса , полученной при вращении звена ломаной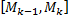

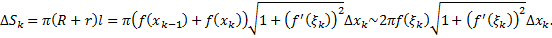
Отсюда площадь поверхности вращения

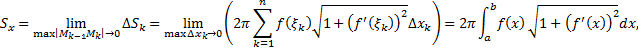
или

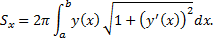
(при 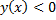надо брать ).

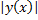Случай кривой, заданной параметрическими уравнениями:

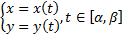
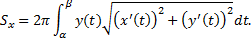
Случай кривой, заданной в полярных координатах:

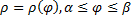
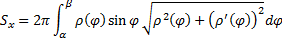
Аналогично при вращении вокруг оси :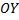

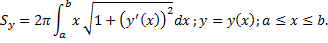
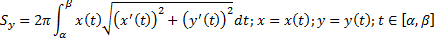
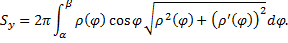
Случай произвольной оси вращения:

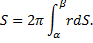
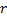– расстояние от переменной точки кривой до оси вращения; 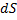– дифференциал дуги.

⇐ Предыдущая 8 9 10 11 121314 15 16 17 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.