Хелпикс

Главная

Контакты

Случайная статья



Сведение ДУ Бернулли к ЛНДУ.. ДУ n-го порядка. Частные и общее решения. Задача Коши, ее геометрическая интерпретация при n=2. Теорема существования и единственности решения задачи Коши. Краевая задача.. Задача Коши для ДУ n-го порядка. Теорема существован

⇐ ПредыдущаяСтр 17 из 28Следующая ⇒


Сведение ДУ Бернулли к ЛНДУ.

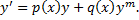
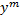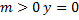Разделим на  (при  – решение):

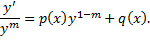
Пусть , тогда ,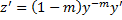

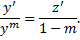
Подставим в ДУ:

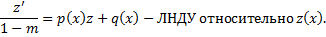
Пример.

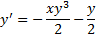
(ДУ Бернулли при 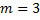;  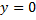– решение).

Разделим на

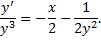
Замена

Подставим, получим

.

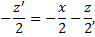
Решая методом вариации постоянной, получим

, т.е.

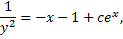
и

.

 

 

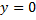2.4. ДУ n-го порядка. Частные и общее решения. Задача Коши, ее геометрическая интерпретация при n=2. Теорема существования и единственности решения задачи Коши. Краевая задача.

 

,

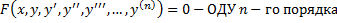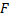 – функция от  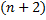переменных.

ДУ n-го порядка, разрешенное относительно старшей производной:

 

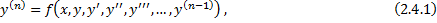
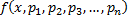 определена в области .

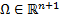Опр. Функция 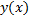 называется частным решением ДУ (2.4.1)на интервале 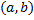, если при ее подстановке в (2.4.1) получается тождество на .

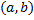Задача Коши для ДУ n-го порядка

Найти частное решение ДУ (2.4.1), удовлетворяющее начальным условиям:

где точка .

При 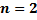 задача Коши имеет вид

,

геометрический смысл: найти интегральную кривую, проходящую через точку 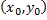 плоскости  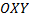и имеющую заданный угловой коэффициент касательной в т. .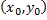

Теорема существования и единственности решения задачи Коши для ДУ n-го порядка

Пусть функция 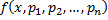 и ее частные производные  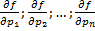непрерывны в области 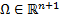. Тогда для  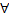точки 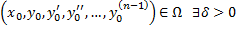, что на интервале  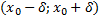существует и при том единственное решение задачи Коши.

Рассмотрим следующий вопрос. Пусть для ДУ n-го порядка выполняется условие существования и единственности. При каких 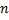 возможно расположение интегральных кривых (см. рис. 35, 36)?

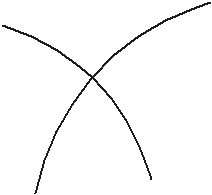Рис. 35 Рис. 36
(Ответ: соответственно .)

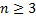Опр. Общим решением ДУ n-го порядка (2.4.1) называется семейство функций , зависящее от 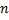 произвольных постоянных  такое, что

1. Для 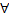 фиксированной  функция 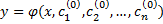 является частным решением ДУ (3).

2. Для 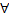 точки 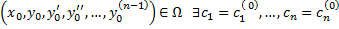 такие, что частное решение  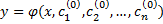удовлетворяет начальным условиям (2.4.2).

Краевая задача для ДУ 2-го порядка: найти частное решение на отрезке [ 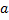, 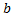] ДУ

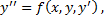
удовлетворяющее краевым условиям

Опр. Равенство , неявно задающее общее решение ДУ n-го порядка называется общим интегралом ДУ n-го порядка.

 


⇐ Предыдущая12131415161718192021Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.