
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Интегрирование периодических функций.
Интегрирование периодических функций.
| Рис. 7 |
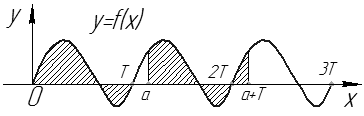 Пусть
Пусть  – периодическая с периодом
– периодическая с периодом 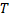 , (т.е.
, (т.е. 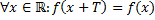 ), интегрируемая на
), интегрируемая на 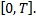 Тогда
Тогда 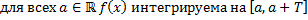 и
и
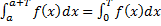 (см. рис. 7).
(см. рис. 7).
1.7. Несобственные интегралы 1-го и 2-го рода, их свойства. Признаки сходимости. Абсолютная и условная сходимость несобственных интегралов.
Несобственные интегралы 1-го рода
Пусть  определена на
определена на 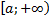 и интегрируема на любом отрезке вида
и интегрируема на любом отрезке вида  . Зафиксируем
. Зафиксируем 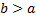 и рассмотрим определенный интеграл
и рассмотрим определенный интеграл 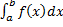 .
.
Опр. Несобственным интегралом 1 рода функции  от
от 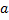 до
до 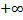 называется предел при
называется предел при 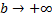 определенного интеграла от
определенного интеграла от 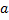 до
до 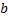 :
:

| Рис. 8 |
 Если
Если 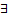 конечный предел
конечный предел 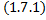 , то несобственный интеграл от
, то несобственный интеграл от 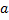 до
до 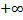 называется сходящимся, в противном случае (т.е. если предел
называется сходящимся, в противном случае (т.е. если предел 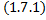 равен
равен 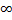 или не существует) – расходящимся.
или не существует) – расходящимся.
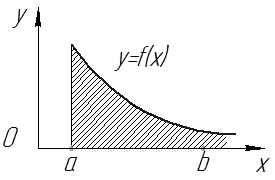
Геометрический смысл – площадь бесконечной фигуры, ограниченной линиями 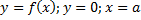 (см. рис. 8).
(см. рис. 8).
| Рис. 9 |
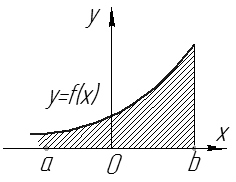
 , определенной на
, определенной на 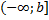 по определению
по определению
 (см. рис. 9).
(см. рис. 9).
Свойство линейности.
Если 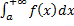 ,
, 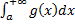 сходятся, то сходятся интегралы
сходятся, то сходятся интегралы
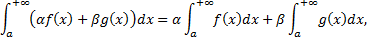
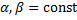 .
.
Аналогично для 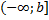 .
.
Вычисление несобственного интеграла 1-го рода.
Пусть 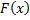 – первообразная для
– первообразная для 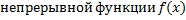 на
на 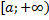 , тогда
, тогда
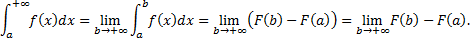
Таким образом, 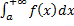 сходится
сходится 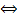
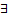 конечный предел первообразной
конечный предел первообразной 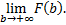
Примеры.
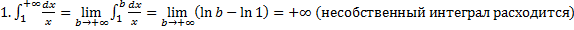 ,
, 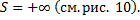
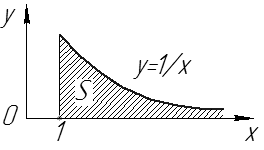
Рис. 10

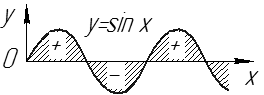
Рис. 11
3. 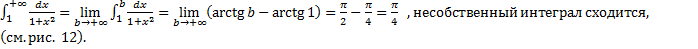
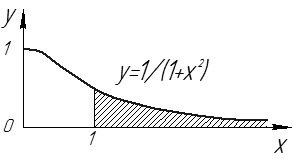
Рис. 12
4. 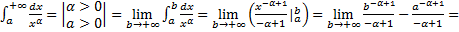
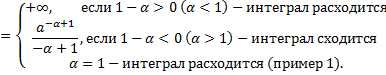
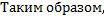

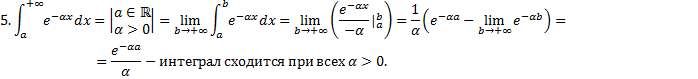
Исследование несобственных интегралов 1-го рода на сходимость.
| Рис. 13 |
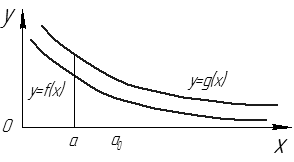 Признаки сходимости:
Признаки сходимости:
1. Признак сравнения.
Пусть 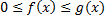
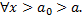
a. Если 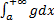 сходится, то
сходится, то 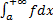 также сходится (см. рис. 13).
также сходится (см. рис. 13).
b. Если 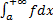 расходится, то
расходится, то 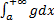 также расходится.
также расходится.
2. Предельный признак сравнения:
пусть для 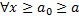
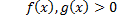 и
и 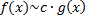 при
при 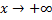 , т.е.
, т.е.  .
.
Тогда 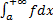 и
и 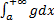 оба сходятся или оба расходятся.
оба сходятся или оба расходятся.
3. Если сходится 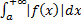 , то сходится и
, то сходится и 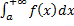 (обратное неверно!).
(обратное неверно!).
В качестве «образцов» интегралов для сравнения обычно используются интегралы
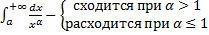 (a>0).
(a>0).
Примеры.
1. 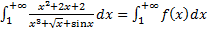 .
.
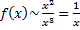 при
при 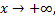
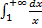 расходится
расходится 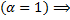 исходный интеграл расходится по предельному признаку.
исходный интеграл расходится по предельному признаку.

При 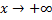
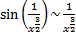 ;
; 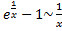 ;
; 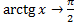 ,
,
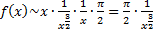 ;
; 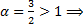 интеграл сходится по предельному признаку.
интеграл сходится по предельному признаку.
3. 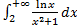
Т.к. при 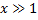
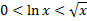 (логарифм растет медленней степенной функции), то
(логарифм растет медленней степенной функции), то 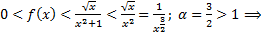 исходный интеграл сходится по признаку сравнения.
исходный интеграл сходится по признаку сравнения.
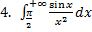 .
.
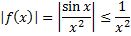
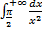 – сходится
– сходится 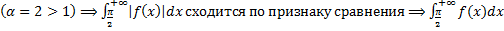 сходится по признаку 3.
сходится по признаку 3.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|