Хелпикс

Главная

Контакты

Случайная статья



Примеры несобственных интегралов с несколькими особыми точками

⇐ ПредыдущаяСтр 11 из 28Следующая ⇒


Примеры несобственных интегралов с несколькими особыми точками

1.

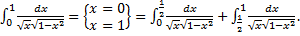
Исходный интеграл сходится, если сходятся оба интеграла в правой части:

a. .

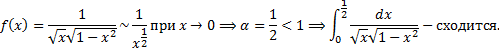
b. .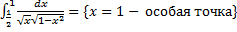

.

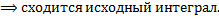
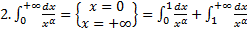(несобственный интеграл 2-го рода 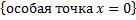+ несобственный интеграл 1-го рода ).

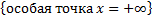a. 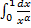 – сходится при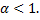

b. 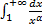 – сходится при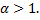

Значит,  расходится для любого .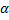

.

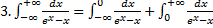a.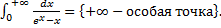

При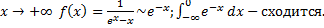

b.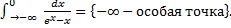

При .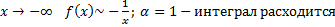

Таким образом исходный интеграл расходится.

Абсолютная и условная сходимость несобственных интегралов.

Рассмотрим несобственный интеграл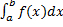

Опр. Несобственный интеграл 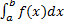называется абсолютно сходящимся, если сходится интеграл .

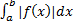Опр. Несобственный интеграл 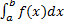называется условно сходящимся, если он сходится, но интеграл  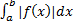расходится.

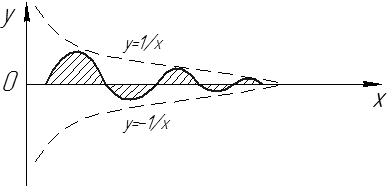
Пример.

 (без доказательства, см. рис. 17).

                                               Рис. 17

 

 

1.8. Вычисление площадей плоских фигур в декартовых и полярных координатах.

 

                                               Рис. 18
Вычисление площадей плоских фигур в декартовых координатах

 непрерывна на

Найдем площадь фигуры, ограниченной линиями 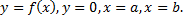 Пусть 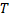 – разбиение отрезка  на элементарные отрезки ; ; .

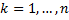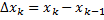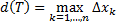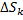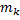Рассмотрим площадь  части фигуры, удовлетворяющей условию . Пусть  и 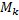 – соответственно наименьшее и наибольшее значения функции  на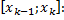

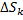 заключена между площадями прямоугольников с высото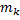й  и

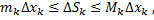
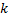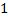Сложим по  от  до :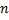

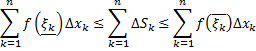
Т.е.

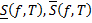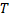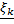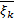где  – интегральные суммы, соответствующие разбиению  и выбору точек  и  соответственно (нижняя и верхняя интегральные суммы Дарбу); при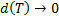

Из (1.9.1) получаем: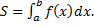

 

Замечания:

1. 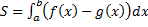 (см. рис. 19.)

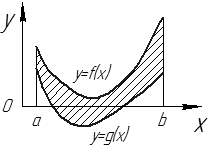
Рис. 19

2. 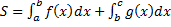 (см. рис. 20).

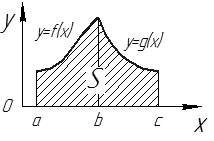
Рис. 20

 

3. 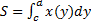 (см. рис. 21).

Рис. 21


⇐ Предыдущая6789101112131415Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.