
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Несобственные интегралы 2-го рода
Несобственные интегралы 2-го рода
| Рис. 14 |
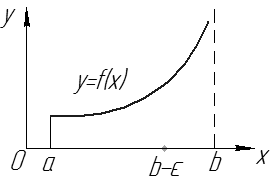 Пусть
Пусть  непрерывна на
непрерывна на  , но не ограничена в левой окрестности точки
, но не ограничена в левой окрестности точки  . Определенный интеграл
. Определенный интеграл  не существует, т.к.
не существует, т.к.  – неограниченная. Рассмотрим
– неограниченная. Рассмотрим 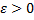 . Т.к.
. Т.к.  непрерывна на
непрерывна на 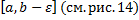 , то
, то 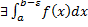 – определенный интеграл.
– определенный интеграл.
Опр. Несобственным интегралом 2 рода по 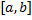 от функции
от функции  , неограниченной в окрестности точки
, неограниченной в окрестности точки 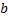 , называется предел
, называется предел
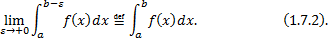
Если существует конечный предел (1.8.2), то несобственный интеграл 2-го рода называется сходящимся, в противном случае – расходящимся.
Геометрический смысл:
при  – площадь фигуры, ограниченной линиями
– площадь фигуры, ограниченной линиями  (см. рис. 15).
(см. рис. 15).
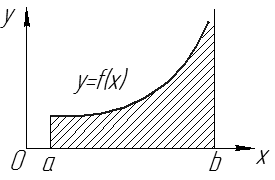
Рис. 15
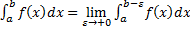 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой 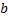 .
.
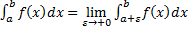 – несобственный интеграл 2-го рода для функции с особой точкой
– несобственный интеграл 2-го рода для функции с особой точкой 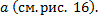
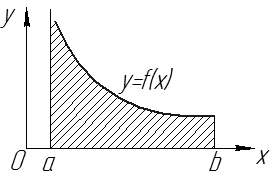
Рис. 16
Свойство линейности.
Если 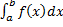 ,
, 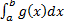 сходятся, то сходятся интегралы
сходятся, то сходятся интегралы
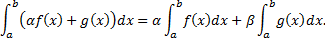
 .
.
Вычисление несобственного интеграла 2-го рода.
Случай функции с особой точкой 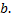
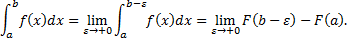
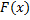 – первообразная для
– первообразная для 
Таким образом, 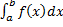 сходится
сходится 
 конечный предел первообразной
конечный предел первообразной 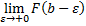 .
.
Примеры.
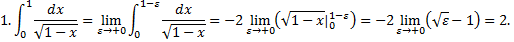
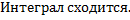
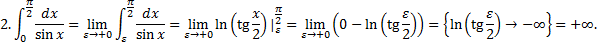
Рассмотрим интегралы
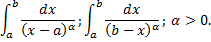
Рассмотрим случай интеграла с особой точкой в левом конце отрезка:
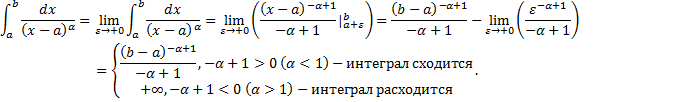
Случай 
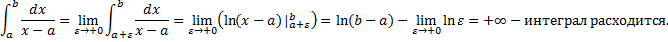
Аналогично рассматривается интеграл с особой точкой в правом конце отрезка. Таким образом
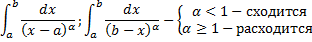
 имеет при
имеет при  порядок роста
порядок роста 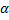 относительно
относительно 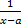 ).
).
Исследование несобственных интегралов 2-го рода на сходимость.
Признаки сходимости:
1. Признак сравнения:
пусть 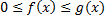
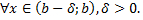
a. Если 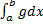 сходится, то
сходится, то 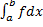 также сходится.
также сходится.
b. Если 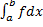 расходится, то
расходится, то 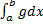 также расходится.
также расходится.
2. Предельный признак сравнения.
Пусть для 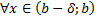
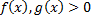 и
и 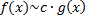 при
при 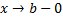 , т.е.
, т.е. 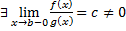 .
.
Тогда 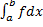 и
и 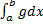 оба сходятся или оба расходятся.
оба сходятся или оба расходятся.
3. Если сходится 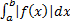 , то сходится и
, то сходится и 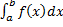 .
.
Примеры.
1.
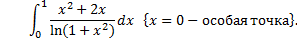
При 
 ,
,
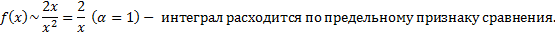
2.
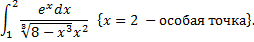
При 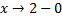
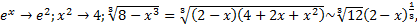
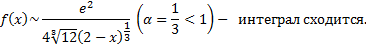
Замечание: если  непрерывна на
непрерывна на  кроме точки
кроме точки 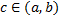 и
и  не ограничена в окрестности точки
не ограничена в окрестности точки 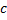 , тогда
, тогда
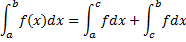
(для первого и второго интегралов в правой части особой точкой является 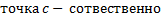 правый или левый конец отрезка).
правый или левый конец отрезка).
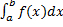 сходится
сходится  сходятся оба интеграла
сходятся оба интеграла 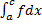 и
и 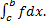
Пример.
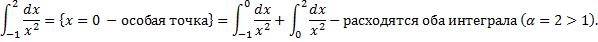
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|