
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вычисление площадей плоских фигур в полярных координатах.
Вычисление площадей плоских фигур в полярных координатах.
Рассмотрим кривую, 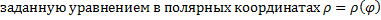 , где функция
, где функция  непрерывна на
непрерывна на 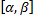 .
.
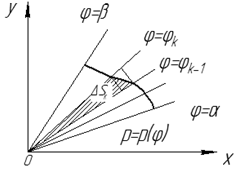
Рис. 22
Найдем площадь фигуры, ограниченной линиями 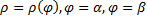 . Пусть
. Пусть 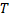 – разбиение
– разбиение 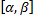 :
:
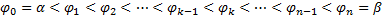
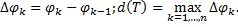
Рассмотрим площадь 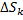 части фигуры, удовлетворяющей условию
части фигуры, удовлетворяющей условию 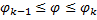 (см. рис. 22). Пусть
(см. рис. 22). Пусть 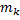 и
и 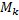 – соответственно наименьшее и наибольшее значения функции
– соответственно наименьшее и наибольшее значения функции 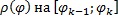 :
:
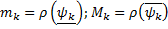 .
.
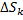 заключена между площадями круговых секторов радиусов
заключена между площадями круговых секторов радиусов 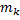 и
и 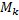 :
:
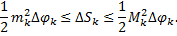
Сложим по 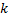 от
от 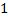 до
до 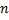 :
:
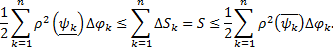
Т.е.

где 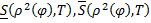 – интегральные суммы функции
– интегральные суммы функции 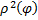 , соответствующие разбиению
, соответствующие разбиению 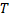 и выбору точек
и выбору точек 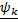 и
и  соответственно (нижняя и верхняя интегральные суммы).
соответственно (нижняя и верхняя интегральные суммы).
При 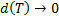 из (1.9.2) получаем:
из (1.9.2) получаем: 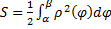 .
.
Замечания:
1. 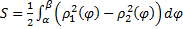 (см. рис. 23).
(см. рис. 23).

Рис. 23
2. 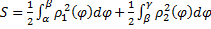 (см. рис. 24).
(см. рис. 24).
Рис. 24
1.9. Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения.
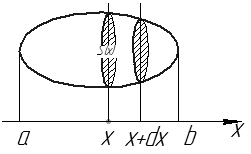
Рис. 25
Рассмотрим в пространстве тело  , каждая точка
, каждая точка  которого удовлетворяет неравенству
которого удовлетворяет неравенству 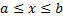 . Пусть площадь сечения
. Пусть площадь сечения  плоскостью
плоскостью  равна
равна 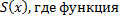
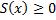 непрерывна на
непрерывна на 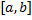 . Найдем объем
. Найдем объем  тела
тела  . Зафиксируем
. Зафиксируем 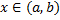 . Рассмотрим малое
. Рассмотрим малое 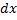 . Рассмотрим часть (слой) тела
. Рассмотрим часть (слой) тела  , соответствующий отрезку
, соответствующий отрезку 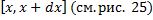 . Объем этой малой части
. Объем этой малой части  приблизительно (c точностью до бесконечно малых выше первого порядка относительно
приблизительно (c точностью до бесконечно малых выше первого порядка относительно 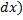 равен объему цилиндра с площадью основания
равен объему цилиндра с площадью основания 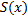 и высотой
и высотой 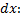
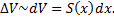
Суммируя по всем таким тонким слоям, получаем
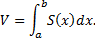
Объемы тел вращения.
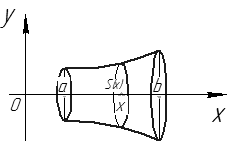
Рис. 26
Фигура, ограниченная линиями 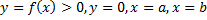 , вращается вокруг оси
, вращается вокруг оси 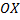 (см. рис. 26).
(см. рис. 26).
Найдем объем 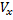 тела вращения. Зафиксируем
тела вращения. Зафиксируем 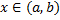 . Сечение тела плоскостью
. Сечение тела плоскостью  – круг радиуса
– круг радиуса 
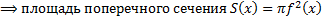 . Тогда
. Тогда

Ту же фигуру вращаем вокруг оси 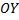 (см. рис. 27).
(см. рис. 27).
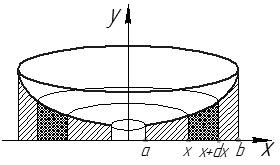
Рис. 27
Рассмотрим малый отрезок  , где
, где 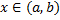 . При вращении соответствующей части фигуры получаем тело объема
. При вращении соответствующей части фигуры получаем тело объема 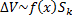 , где
, где 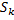 – площадь кольца радиусов
– площадь кольца радиусов 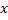 и
и 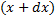 соответственно:
соответственно:
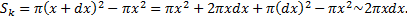
Тогда
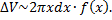
Суммируя по тонким "слоям", получим
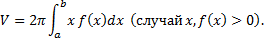
Общий случай:
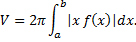
Таким образом получаем для вращения фигуры, ограниченной линиями  , имеем
, имеем
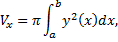
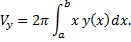
При вращении фигуры, ограниченной линиями 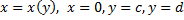 (см. рис. 28).
(см. рис. 28).

Рис. 28
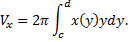
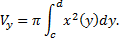
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|