
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определенный интеграл с переменным верхним пределом. Теорема о производной интеграла с переменным верхним пределом. Формула Ньютона-Лейбница.
1.5. Определенный интеграл с переменным верхним пределом. Теорема о производной интеграла с переменным верхним пределом. Формула Ньютона-Лейбница.
Пусть  интегрируема на
интегрируема на  . Зафиксируем
. Зафиксируем 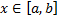 . Рассмотрим определенный интеграл по
. Рассмотрим определенный интеграл по 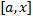 :
:
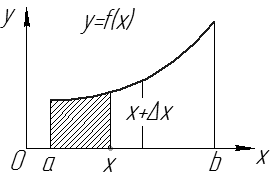
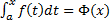 – определенный интеграл с переменным верхним пределом (см. рис. 5).
– определенный интеграл с переменным верхним пределом (см. рис. 5).
Теорема (о производной интеграла с переменным верхним пределом).
Пусть  непрерывна на
непрерывна на  . Тогда
. Тогда 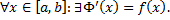
| Рис. 5 |
 Док-во:
Док-во: 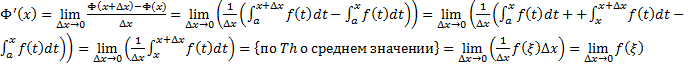 , где
, где 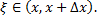
При 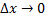
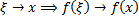 , (т.к.
, (т.к. 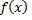 – непрерывная функция) т.е.
– непрерывная функция) т.е. 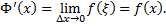

Следствие: если  непрерывна на
непрерывна на  , то на
, то на  существует ее первообразная
существует ее первообразная 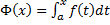 . Любая первообразная имеет вид
. Любая первообразная имеет вид 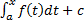 .
.
Пример.
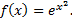
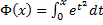 – первообразная для
– первообразная для 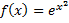 (не выражается через элементарные функции, интеграл – неберущийся).
(не выражается через элементарные функции, интеграл – неберущийся).
Формула Ньютона-Лейбница.
Пусть  непрерывна на
непрерывна на  ,
, 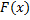 – ее первообразная. Тогда
– ее первообразная. Тогда 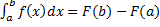 .
.
Док-во: пусть 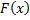 – произвольная первообразная. Рассмотрим
– произвольная первообразная. Рассмотрим 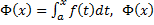 – также первообразная. Тогда
– также первообразная. Тогда 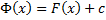 . Возьмем
. Возьмем 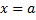 . Т.к.
. Т.к. 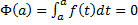 , то
, то 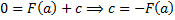 , т.е.
, т.е. 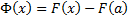 . При
. При  :
: 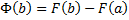 или
или 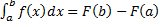 :
:
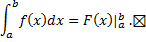
Пример.
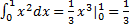 .
.
1.6. Вычисление определенного интеграла подстановкой и по частям. Интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат, интегрирование периодических функций.
Пусть  непрерывна на
непрерывна на  , функция
, функция 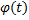 имеет непрерывную производную на
имеет непрерывную производную на 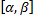 , причем
, причем 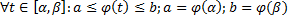 . Тогда
. Тогда 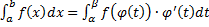 .
.
Док-во: пусть 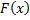 –первообразная для
–первообразная для  на
на  , т.е.
, т.е. 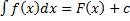 . Тогда по формуле Ньютона-Лейбница:
. Тогда по формуле Ньютона-Лейбница: 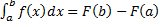 . Функция
. Функция 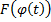 – первообразная для
– первообразная для 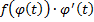 , по формуле Ньютона-Лейбница:
, по формуле Ньютона-Лейбница: 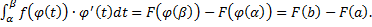
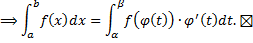
Пример.
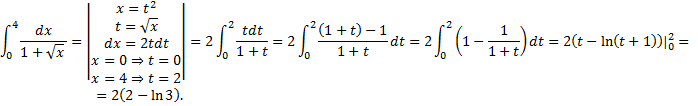
Интегрирование по частям в определенном интеграле.
Пусть функции 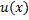 и
и 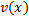 имеют непрерывные производные на [
имеют непрерывные производные на [ 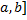 .
.
Тогда  , т.е.
, т.е. 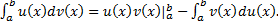
Док-во: 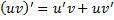 , т.е.
, т.е. 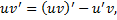
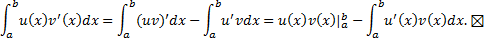
Пример.
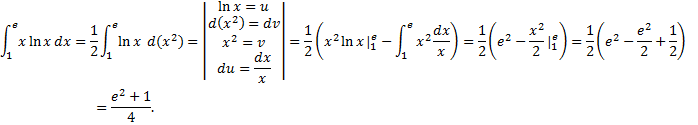
Интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат 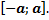
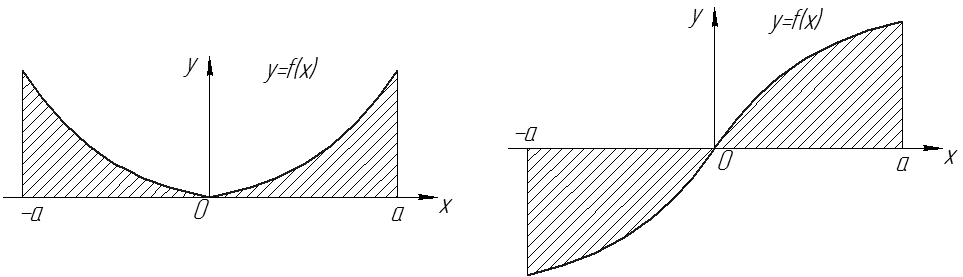
Рис. 6
Теорема. Пусть  интегрируема на
интегрируема на 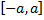 , тогда:
, тогда:
1. Если  – четная, то
– четная, то 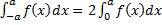 .
.
2. Если  – нечетная, то
– нечетная, то 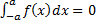 .
.
Док-во: 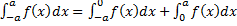 (по свойству аддитивности) (см. рис. 6).
(по свойству аддитивности) (см. рис. 6).
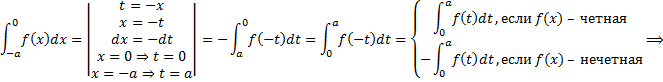
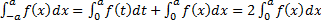 – для четной функции,
– для четной функции,
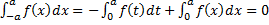 – для нечетной функции.
– для нечетной функции.
Пример.
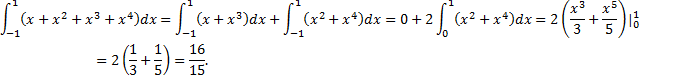
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|