Хелпикс

Главная

Контакты

Случайная статья



Свойства определенного интеграла

⇐ ПредыдущаяСтр 7 из 28Следующая ⇒


Свойства определенного интеграла

1. Линейность

Пусть функци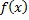и  и 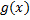 интегрируемы н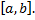а  Тогда

a. функция 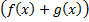 интегрируема на  и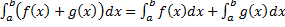

b. функция 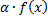 ( 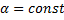) интегрируема на  и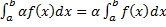

Док-во:

a. составим интегральную сумму для функции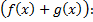

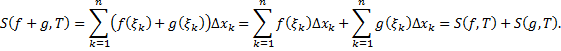
Тогда

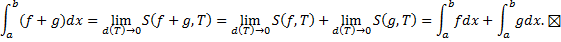
b. Аналогично

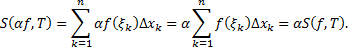
Тогда

 

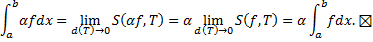
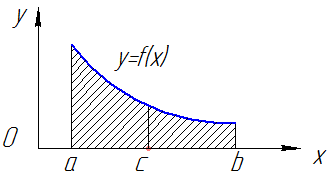
2. Аддитивность (см. рис. 3).

Пусть функция  интегрируема на , точка 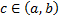, тогда

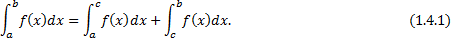
Док-во:

Рассмотрим разбиение 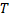 отрезка  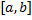такое, что  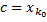для некоторого 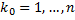. Ему соответствуют разбиения отрезков  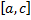и 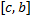, соответственно,  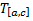и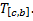

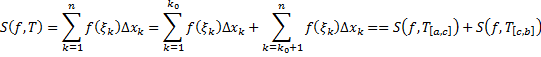
                                  Рис. 3

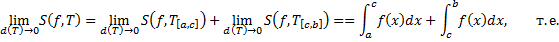
Т.е.

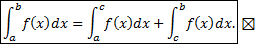
Замечание. Если 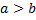, то по определению ,

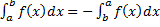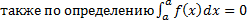. Тогда равенство (1.4.1) справедливо при любом взаимном расположении точек ,

 

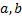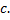
Теорема (об оценке определенного интеграла)

Пусть  интегрируема на , .

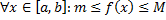Тогда

                   .

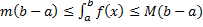Док-во: 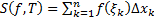. Т.к. 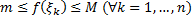, то ,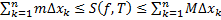

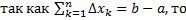
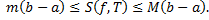
При  получим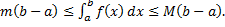

                                     Рис. 4
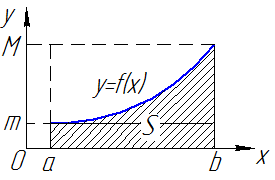Геометрическая интерпретация:

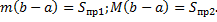
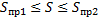 (площаль криволинейной трапеции заключна между площадьми прямоугольников высотой m и M.) (см. рис. 4).

Следствиe (интегрирование неравенства).

Пусть 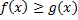 на , тогда .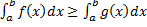

Док-во: рассмотрим функцию 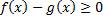 на . Возьмем 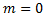. По теореме об оценке

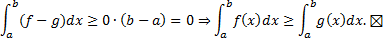
Пример.

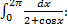 т.к. , то 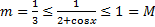. По теореме об оценке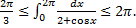

 

Теорема (о среднем значении для определенного интеграла).

Пусть  непрерывна на . Тогда 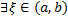 такая, что .

Док-во: т.к. 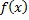 непрерывна на , то она достигает на  своего наибольшего и наименьшего значений 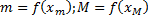,  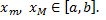По теореме об оценке 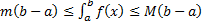, (равенство возможно только для т.е. для непрерывных функций, отличных от константы 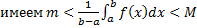. По теореме о промежуточном значении непрерывной функции: 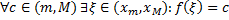. Возьмем .

 

 


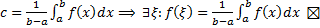⇐ Предыдущая234567891011Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.