Контакты

Случайная статья

Определенный интеграл как предел интегральных сумм.

⇐ ПредыдущаяСтр 6 из 28Следующая ⇒

Определенный интеграл как предел интегральных сумм.

Пусть функция определена на .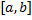

Опр. Разбиением 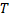отрезка 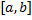называется совокупность точек 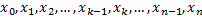, где .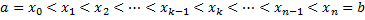

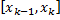– элементарный отрезок ( ),

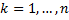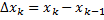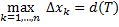, – диаметр разбиения .

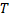Выберем произвольные точки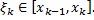

Рис. 1

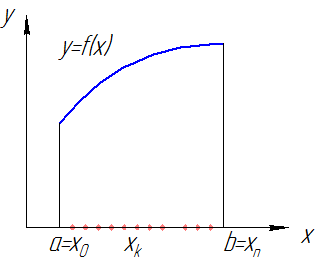Опр. Интегральной суммой функции

, соответствующей разбиению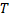

отрезка

и выбору точек

(

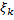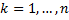) называется величина

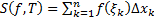(см. рис. 1).

Опр. Определенным интегралом функции на отрезке называется конечный предел при 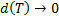интегральных сумм 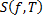, если он существует и не зависит от способа разбиения отрезка и выбора точек .

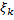Обозн.: 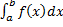, т.е.

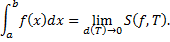
Тогда масса неоднородного стержня: 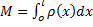; координата точки: .

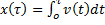Опр. Если для функции существует 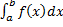, то функция называется интегрируемой (по Риману) на .

Теорема (необходимое условие интегрируемости.)

Пусть функция интегрируема на , тогда ограничена на .

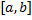Теорема (достаточное условие интегрируемости 1).

Непрерывная на функция является интегрируемой на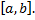

Теорема (достаточное условие интегрируемости 2).

Пусть 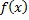непрерывна на кроме конечного числа точек разрыва первого рода , тогда является интегрируемой на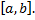

Геометрическая интерпретация определенного интеграла. 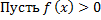, непрерывна на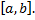

Рис. 2

.

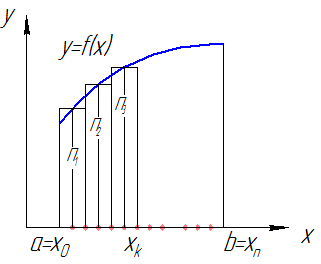
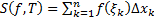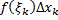– площадь прямоугольника 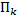со сторонами 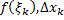(см. рис. 2).

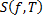– площадь ступенчатой фигуры

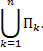
При 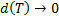получим площадь криволинейной трапеции, ограниченной графиком функции 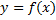сверху, осью 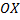снизу и прямыми .

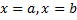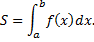
⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.