Контакты

Случайная статья

Интегрирование простейших дробей 1-3 типов.

⇐ ПредыдущаяСтр 5 из 28Следующая ⇒

Интегрирование простейших дробей 1-3 типов.

1.

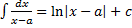
2.

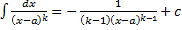
3. 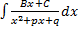– выделить в числителе производную трехчлена.

Пример.

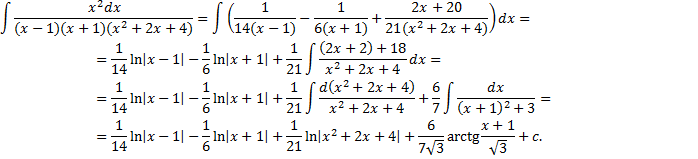
Интегрирование простейших дробей 4 типа.

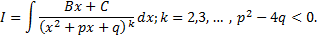
Выделим полный квадрат: 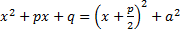("+ "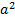, т.к. иначе трехчлен имел бы корни)

Замена 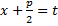. Тогда

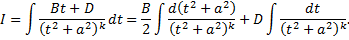
Рассмотрим .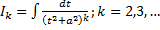

Получим формулу понижения, выражающую 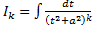через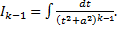

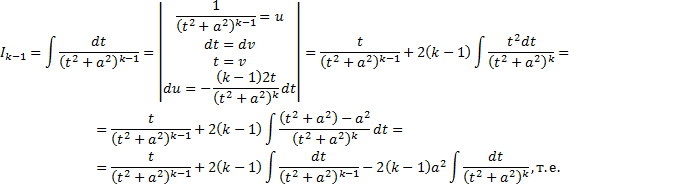
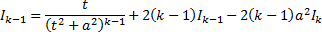
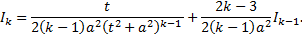
Пример.

.

.

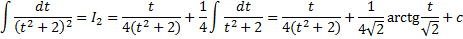
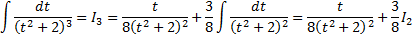
Алгоритм интегрирования рациональных дробей.

1. Если 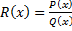– неправильная рациональная дробь, то представить ее в виде суммы многочлена и правильной рациональной дроби:

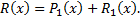
2. Представить 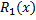согласно (1.3.2) в виде суммы простейших дробей с неопределенными коэффициентами.

3. Найти неопределенные коэффициенты.

4. Проинтегрировать сумму простейших дробей.

1.4. Определенный интеграл, его механический и геометрический смысл, теорема существования. Линейность и аддитивность определенного интеграла.

Задача о массе неоднородного стержня.

Стержень длины 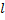имеет плотность 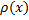. Найти массу .

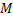Разобьем стержень на малые участки: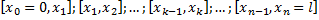

Тогда можно считать каждый участок 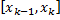однородным, и масса k-го участка

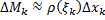, где 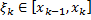, 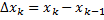. Тогда масса стержня

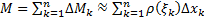. Перейдя к пределу при , получим точное значение массы

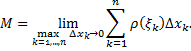
Вычисление координаты точки, движущейся с переменной скоростью. Рассмотрим точку, движущуюся по прямой с переменной скоростью 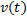. Пусть начальная координата точки равна 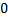. Найти координату точки в момент времени .

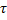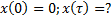
Разобьем интервал времени 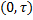на малые интервалы:

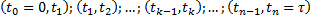
Считая, что за малый интервал 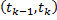скорость не меняется, получаем изменение координаты за этот интервал:

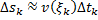, где ,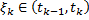

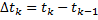
Тогда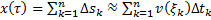

Точное значение:

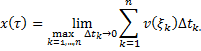
⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.