Контакты

Случайная статья

Интегрирование иррациональных функций.

⇐ ПредыдущаяСтр 4 из 28Следующая ⇒

Интегрирование иррациональных функций.

I. .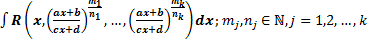

Замена 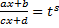, 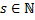–общий знаменатель (Н.О.К. ).

Пример.

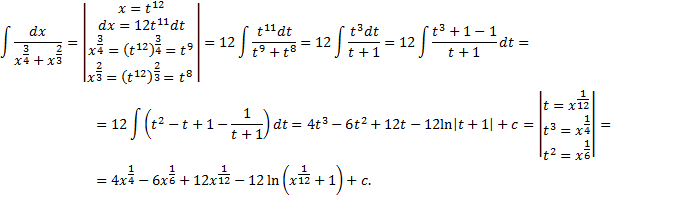
II.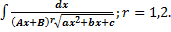

Замена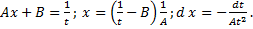

Пример.

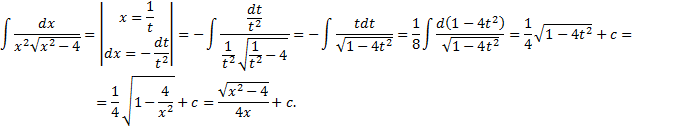
III. .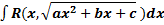

Выделив полный квадрат, получим интеграл одного из видов:

a)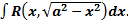

Замена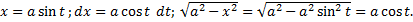

Пример.

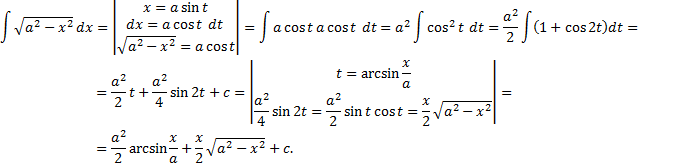
b) .

Замена .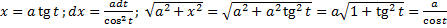

Пример.

c) .

Замена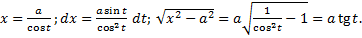

Пример.

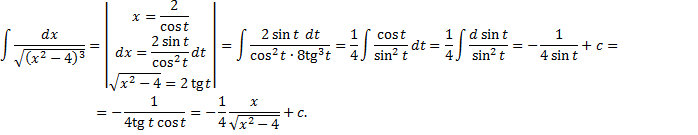
Примеры интегралов, не выражающихся через элементарные функции:

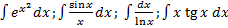( «неберущиеся» интегралы).

1.3. Интегрирование рациональных дробей. Разложение правильной рациональной дроби в сумму простейших. Интегрирование простейших дробей. Интегрирование неправильных рациональных дробей.

Рациональная дробь

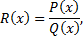
где

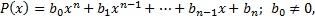
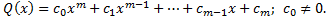
Опр. Рациональная дробь 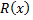называется правильной, если .

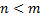Опр. Рациональная дробь 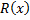называется неправильной, если .

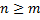Пусть 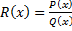– неправильная дробь. Разделим с остатком 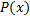на 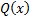, т.е. представим 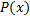в ви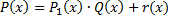де , где 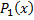– многочлен степени 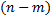, степень многочлена меньше 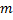. Тогда 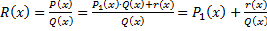, где 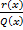– правильная рациональная дробь.

Пример.

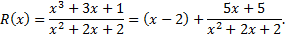
Разложение многочлена на множители. Пусть

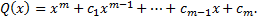
Тогда
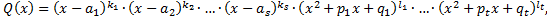(1.3.1)

где 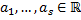– корни многочлена 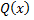кратности 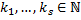соответственно,

.

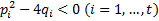Пример.

.

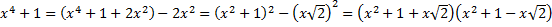Простейшие рациональные дроби.

Опр. Простейшими называют рациональные дроби одного из следующих видов:

1.

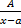
2.

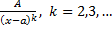
3.

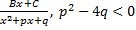
4.

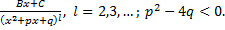
Разложение правильной рациональной дроби в сумму простейших.

Пусть 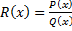– правильная рациональная дробь, 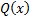разложен по формуле (1.3.1). Тогда 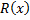можно представить в виде суммы простейших дробей:

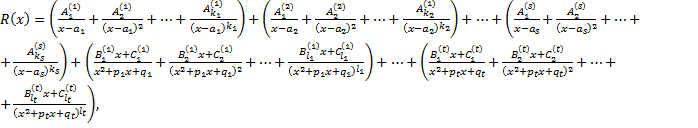(1.3.2)

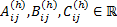– неопределенные коэффициенты.

Пример.

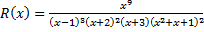– правильная дробь.

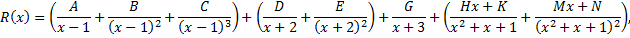
– неопределенные коэффициенты.

Пример (определение коэффициентов).

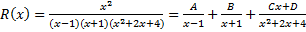. (1.3.3)

Найдем 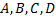. Приведем слагаемые в правой части (1.3.3) к общему знаменателю:

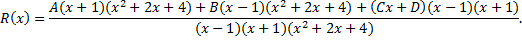
Приравняем числители полученной дроби и исходной дроби :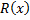

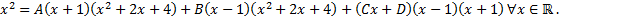(1.3.4)

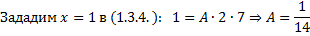
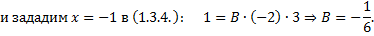
Приравняем коэффициенты при 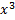в (1.3.4):

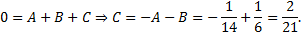
Приравняем коэффициенты при 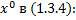, т.е. :

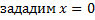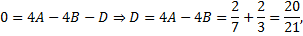
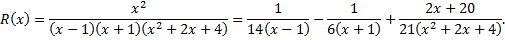
⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.