Хелпикс

Главная

Контакты

Случайная статья



Подведение под знак дифференциала.

⇐ ПредыдущаяСтр 3 из 28Следующая ⇒


Подведение под знак дифференциала.

Пусть 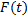 – первообразная функции  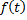на 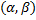, т.е. 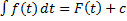. Рассмотрим замену 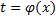, где 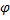 – дифференцируемая на  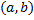функция, .

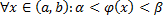Рассмотрим сложную функцию , .

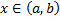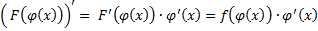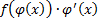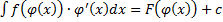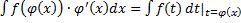, т.е.  – первообразная для , т.е. , или , или ,

                       

Примеры.

1.

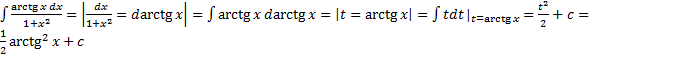
2.

3. .

 

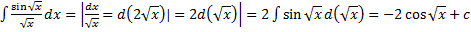Замена переменной. Поменяем в (1.2.1) местам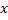и  и :  ,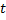

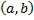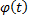где  определена на ,  дифференцируема на 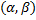, причем .

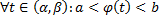Пусть 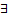 обратная функция  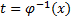. Заменим  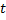на :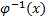

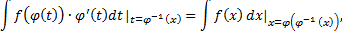
Т.е.

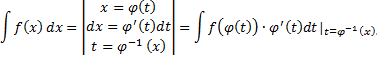
Пример.

Интегрирование по частям

Пусть функци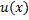и  и 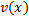 дифференцируемы на 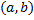. Тогда 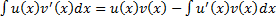, т.е.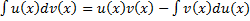

Док-во: 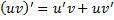, т.е.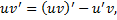

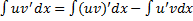, т.е. ,

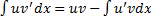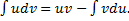
Примеры.

1. .

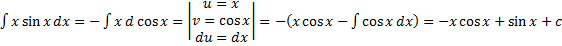2. .

3. ,

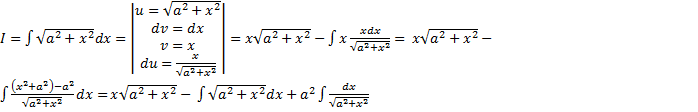 т.е. 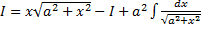, т.е.

.

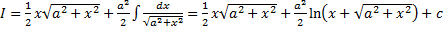Интегрирование выражений, содержащих квадратный трехчлен

I.  , .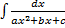

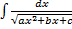Выделим полный квадрат, получим табличный интеграл (10-13)

Примеры.

1. .

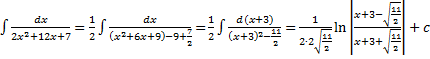2. .

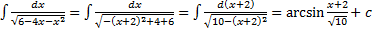II. , .

Выделим в числителе производную квадратного трехчлена 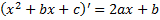, т.е. представим числитель в виде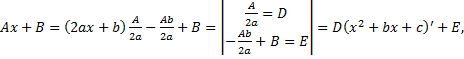

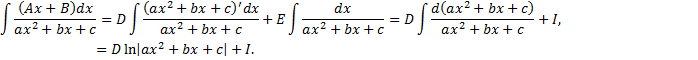
где 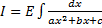 – находится с помощью выделения полного квадрата.

Аналогично

 

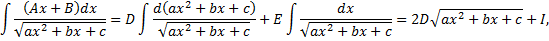
где  .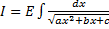

Примеры.

1.

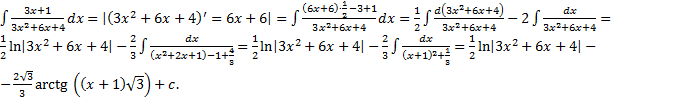
2.

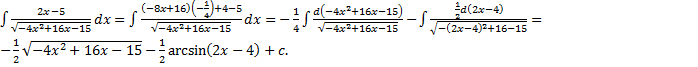
Интегрирование тригонометрических функций.

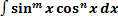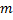1. , где  или 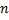 – нечетное натуральное число (например, )

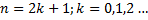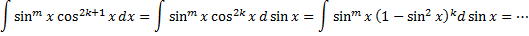
Пример.

2. 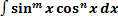  , где 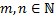 – четные. Используем формулы понижения степени

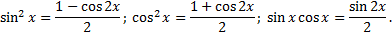
Пример.

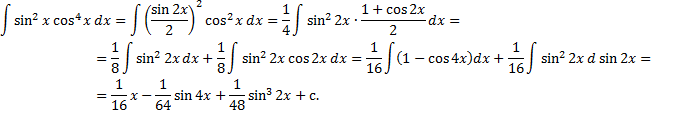
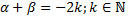3.  где (т.е. 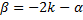 ). Используем формулы

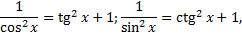
Пример.

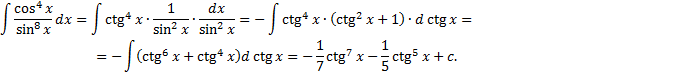
4. 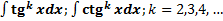 . Понижение показателя с использованием формул

 

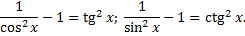
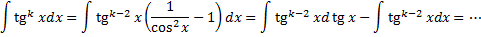
Пример. 

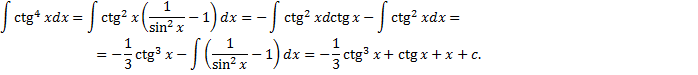
5.  где 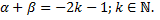Понижение степени с использованием формул:

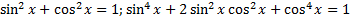 и т.д.

 Пример.

 

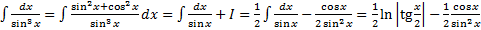 +c,

Где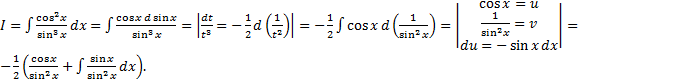

6.

Преобразование произведения тригонометрических функций в сумму.

7. 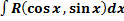, где  .

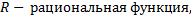
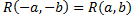Подстановка .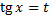

Пример.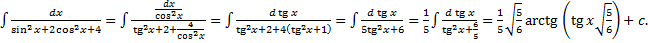  

8. 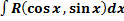,где .

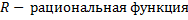Подстановка ,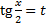

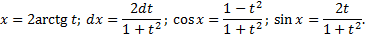
Пример.


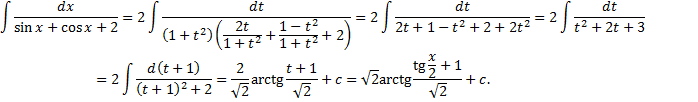
⇐ Предыдущая12345678910Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.